Лекция
Переходные процессы в колебательных контурах
Орел 2009
Содержание
Вступление
Переходные колебания в параллельном контуре
Свободные колебания в параллельном контуре
Режимы переходных колебаний в колебательных контурах
Переходные колебания при гармоническом воздействии
Литература
Вступление
Колебательные контуры составляют значительную часть аппаратуры связи. Они могут выполнять самые различные функции: например, участвовать в выделении гармонических колебаний из последовательности видеоимпульсов, в формировании прямоугольных импульсов заданной длительности и др. На практике довольно распространен случай, когда на контур действует прямоугольный импульс (рис. 1).
Рис. 1
Если предположить 
, то нетрудно видеть, что при 
в контуре будет наблюдаться режим переходных колебаний, а с момента 
– свободные колебания за счет запасенной реактивными элементами энергии. Рассмотрим оба этих случая на примере параллельного контура.
Переходные колебания в параллельном контуре
Пусть на параллельный контур, находящийся при ННУ, в момент 
действует перепад тока величиной 
. Требуется определить реакцию – временную зависимость напряжения на контуре (рис. 2а).
а) б)
Рис. 2
Для нахождения 
воспользуемся операторной схемой замещения, показанной на рис. 2,б. Найдем 
:
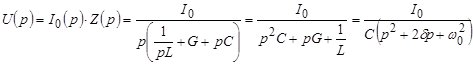
где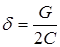 
– есть коэффициент затухания;
– частота собственных незатухающих колебаний.
Воспользуемся таблицей соответствий (Л.0.1, стр. 222):
,
где 
– частота собственных затухающих колебаний.
График имеет вид:
Рис. 3
Свободные колебания в параллельном контуре
Пусть в момент в схеме, показанной на рисунке 4а гасится источник тока . Требуется определить временную зависимость напряжения на контуре.
Примечание: Такая задача возникает после окончания действия прямоугольного импульса (рис. 1) на контур.
а) б) в)
Рис. 4
Для определения начальных условий изобразим эквивалентную схему (рис. 4б) для момента времени, непосредственно предшествующего коммутации. При этом для постоянного тока индуктивность представляется коротким замыканием, а емкость – обрывом цепи. Легко видеть, что до момента гашения весь ток источника будет проходить через индуктивность. Поэтому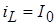 
, 
.
В операторной схеме (рис. 4б) индуктивность отображена схемой замещения с источником тока. Нахождение здесь отличается от предыдущего случая (рис. 2б) лишь направлением операторного источника тока. Следовательно, можно записать:
.
График данной зависимости будет зеркальным отображением зависимости (*), полученной для переходного процесса (рис. 5).
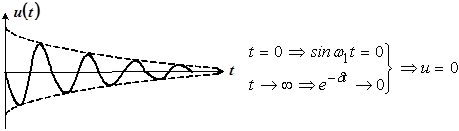
Рис. 5
Можно показать, что аналогичные результаты получаются при анализе переходных и свободных колебаний в последовательном контуре.
Отметим две особенности полученных выражений:
– во-первых, колебания носят гармонический характер, на что указывает множитель гармонической функции 
;
– во-вторых, амплитуда полученных колебаний изменяется во времени по экспоненциальному закону 
.
Очевидно, что вид графиков найденных функций будет зависеть от величины коэффициента затухания 
и его соотношения с 
поскольку последним определяется величина 
.
Поэтому в зависимости от и различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру.