Обобщение принципа оптимальности по Парето.Элементы теории доминирования.Принцип оптимальности по конусу.
Существует более общий подход к проблеме многокритериальной оптимизации, основанный на теории доминирования и использующий в качестве основных такие понятия, как структура доминирования, конус доминирования, оптимальность по конусу.
Рассмотрим задачу многокритериальной оптимизации в виде:
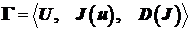 . (1)
. (1)
Определение 1. Каждому элементу 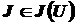 поставим в соответствие множество
поставим в соответствие множество 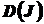 , называемое множеством доминирующих факторов. Если
, называемое множеством доминирующих факторов. Если  таков, что
таков, что 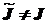 и
и 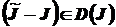 , то будем говорить, что элемент
, то будем говорить, что элемент 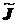 доминирует
доминирует 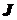 , (или
, (или 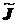 предпочтительнее, чем
предпочтительнее, чем 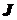 ).
).
Совокупность 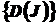 , определенная на всем множестве
, определенная на всем множестве 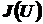 , называется структурой доминирования.
, называется структурой доминирования.
Определение 2. Пусть 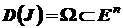 - замкнутый выпуклый конус, с вершиной в точке
- замкнутый выпуклый конус, с вершиной в точке 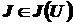 . Если
. Если  таков, что
таков, что 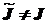 и
и 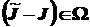 , то будем говорить, что элемент
, то будем говорить, что элемент 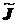 доминирует
доминирует 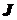 относительно конуса доминирования
относительно конуса доминирования  .
.
Таким образом, с помощью замкнутого выпуклого конуса доминирования можно описать на множестве достижимых векторных оценок 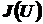 систему бинарных отношений
систему бинарных отношений 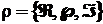 в следующем виде:
в следующем виде:
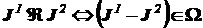 , (2)
, (2)
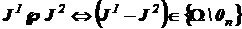 , (3)
, (3)
 . (4)
. (4)
Тогда постановка задачи многокритериальной оптимизации может быть записана в виде
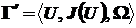 . (5)
. (5)
Определение 3. Векторная оценка  называется
называется  -оптимальной (оптимальной по конусу
-оптимальной (оптимальной по конусу  ) на множестве
) на множестве 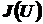 , если не существует
, если не существует 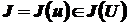 ,
, 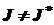 , такой, что
, такой, что  . Соответствующее допустимое решение
. Соответствующее допустимое решение 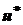 называется
называется  -оптимальным решением задачи (5). Будем обозначать множество всех
-оптимальным решением задачи (5). Будем обозначать множество всех  -оптимальных в
-оптимальных в 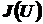 векторных оценок, как
векторных оценок, как  , а множество всех
, а множество всех  -оптимальных решений задачи (5), как соответственно
-оптимальных решений задачи (5), как соответственно 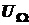 .
.
При 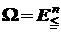 свойство оптимальности по Парето является частным случаем оптимальности по конусу.
свойство оптимальности по Парето является частным случаем оптимальности по конусу.
Конус доминирования имеет ряд полезных свойств.
Теорема 1. Пусть 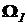 ,
, 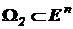 - выпуклые конусы, и
- выпуклые конусы, и 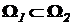 . Тогда в задаче (1.12)
. Тогда в задаче (1.12)
 . (6)
. (6)
Теорема 2.. Пусть 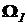 ,
, 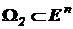 - различные выпуклые конусы. Тогда в задаче (5):
- различные выпуклые конусы. Тогда в задаче (5):
1) 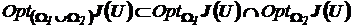 ; (7)
; (7)
2) 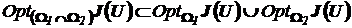 . (8)
. (8)
Если конус доминирования  является полиэдральным, то, как известно, его можно представить в виде системы неравенств:
является полиэдральным, то, как известно, его можно представить в виде системы неравенств:
 , (9)
, (9)
где  - числовая матрица размерности
- числовая матрица размерности  . В этом случае взаимосвязь принципов оптимальности по конусу и оптимальности по Парето устанавливается следующей теоремой.
. В этом случае взаимосвязь принципов оптимальности по конусу и оптимальности по Парето устанавливается следующей теоремой.
Теорема 3. Пусть в задаче многокритериальной оптимизации (5)  - полиэдральный конус доминирования вида (9). Рассмотрим
- полиэдральный конус доминирования вида (9). Рассмотрим 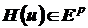 - новый векторный показатель вида
- новый векторный показатель вида
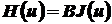 . (10)
. (10)
Тогда оптимальные по Парето точки для векторного показателя 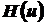 точно совпадают с
точно совпадают с  - оптимальными точками для векторного показателя
- оптимальными точками для векторного показателя  на множестве
на множестве  :
: 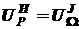 .
.
Вычислительные алгоритмы построения множества
оптимальных по конусу решений в задаче многокритериальной оптимизации.
Метод ЛП-поиска.
Постановку задачи построения множества оптимальных по конусу решений задачи многокритериальной оптимизации представим в виде:
определить 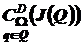 (8)
(8)
То есть требуется определить множество  значений показателя
значений показателя  , являющееся дискретной аппроксимацией ядра
, являющееся дискретной аппроксимацией ядра 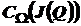 отношения предпочтения, выраженного в форме выпуклого полиэдрального конуса
отношения предпочтения, выраженного в форме выпуклого полиэдрального конуса 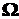 , на множестве достижимых векторных оценок
, на множестве достижимых векторных оценок 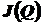 .
.
Для решения задачи (8) предлагается использовать модифицированный алгоритм метода зондирования пространства параметров, основанный на методике ЛП-поиска, и состоящий из двух основных этапов:
1) составление таблицы испытаний;
2) 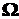 -оптимизация таблицы испытаний.
-оптимизация таблицы испытаний.
Этап 1. Генерируется последовательность точек  , равномерно распределенная в
, равномерно распределенная в 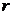 -мерном единичном гиперкубе
-мерном единичном гиперкубе 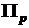 . Наилучшими характеристиками равномерности распределения обладают так называемые ЛП-последовательности. Для генерации ЛП-последовательности предлагается арифметический алгоритм, в котором используется специальная таблица направляющих чисел
. Наилучшими характеристиками равномерности распределения обладают так называемые ЛП-последовательности. Для генерации ЛП-последовательности предлагается арифметический алгоритм, в котором используется специальная таблица направляющих чисел 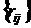 .
.
По заданному номеру  вычисляем
вычисляем
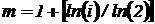 (9)
(9)
Далее для  вычисляем
вычисляем
 , (10)
, (10)
где  ,
, 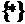 - целая и дробная части аргумента * соответственно.
- целая и дробная части аргумента * соответственно.
После этого с помощью линейного преобразования 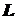 , сохраняющего равномерность распределения, преобразуем множество сгенерированных точек
, сохраняющего равномерность распределения, преобразуем множество сгенерированных точек  в множество точек
в множество точек  , равномерно заполняющих
, равномерно заполняющих  -мерный гиперпараллелепипед
-мерный гиперпараллелепипед 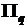 , определяемый верхними и нижними ограничениями на параметры задачи
, определяемый верхними и нижними ограничениями на параметры задачи 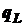 и
и 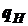 :
:
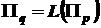 . (11)
. (11)
Преобразование 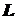 задаем в виде
задаем в виде
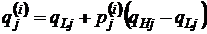 (12)
(12)
Если в точке 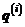 выполняются линейные ограничения общего вида, входящие в описание множества
выполняются линейные ограничения общего вида, входящие в описание множества 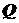 , то точка
, то точка 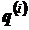 является допустимой. В ней вычисляется
является допустимой. В ней вычисляется  и заносится в таблицу испытаний
и заносится в таблицу испытаний 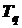 .
.
Этап 2. Осуществляется оптимизация таблицы испытаний по конусу доминирования, заданному в виде (2.5). С этой целью из таблицы 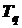 выбирается какая-либо точка
выбирается какая-либо точка 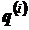 и помечается. Просматривая все точки
и помечается. Просматривая все точки  таблицы
таблицы 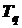 , отличные от
, отличные от 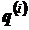 , исключим те из них, для которых
, исключим те из них, для которых
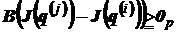 , (13)
, (13)
т.е. проверяется условие
 .
.
Затем среди оставшихся точек выбирается ранее не помеченная, и вновь повторяется процесс исключения по правилу (13). После конечного числа шагов останутся только помеченные точки, принадлежащие множеству 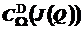 .
.
С увеличением плотности ЛП-сети имеет место:
 .
.
Замечание.
Для построения множества оптимальных по конусу решений может быть использован алгоритм многокритериального ранжирования, рассмотренный ранее.
Слабоструктурированные многокритериальные аналитические задачи. Метод анализа иерархий
Метод анализа иерархий (МАИ) - математический инструмент анализа сложных слабоструктурированных аналитических задач. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению
МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения.
Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне.
Метод основан на декомпозиции задачи и представлении ее в виде иерархической структуры. Это позволяет включить в иерархию все знания по решаемой проблеме. В результате решения определяется численно выраженная относительная степень взаимодействия элементов в иерархии. Решение задачи с помощью МАИ выполняется поэтапно.
Первый этап предусматривает представление проблемы в виде иерархии. В простейшем случае иерархия строится начиная с цели, которая помещается в вершину иерархии, через промежуточные уровни, на которых размещаются критерии и от которых зависят последующие уровни, к самому низшему уровню, который содержит перечень альтернатив.
Второй этап. На этом этапе необходимо установить приоритеты критериев и оценить каждую альтернативу по критериям для выбора из них наиболее важной.
В МАИ элементы сравниваются попарно по отношению к их влиянию на общую для них характеристику.
Для получения положительных результатов в сравнениях необходимо уметь:
- находить соответствующую численную шкалу сравнений;
- определять степень несогласованности наших суждений.
Главное требование к шкале сравнений - шкала должна быть простой и естественной.Шкала Т. Саати построена на основе объективно действующего психофизического закона Вебера-Фехнера и содержит числа от 1 до 9.
Применяется следующий способ практического количественного сравнения объектов, действий или обстоятельств и построения таблицы суждений. Пусть даны элементы A, B, C, D.
| A | B | C | D | |
| A | ||||
| B | ||||
| C | ||||
| D |
Таблица парных суждений (сравнений) строится по следующим правилам: при
сравнении элемента с самим собой заносятся единицы; если А и В одинаково значимы, то в ячейки для А, В таблицы заносится число 1; если А немного важнее В, то в ячейку для В заносится число 3; если А существенно важнее В, то в ячейку для В заносится число 5; если А значительно превосходит В, то в ячейку для В заносится число 7; если А очень сильно превосходит В, то в ячейку для В заносится число 9. Числа 2, 4, 6, 8 используются в компромиссных случаях как промежуточные решения между двумя суждениями. Рациональные дроби используются в случае, если желательно увеличитьсогласованность всей таблицы при малом числе суждений.
Таблицу парных сравнений можно записать в виде обратно симметричной матрицы
 ,
,
в которой  .
.
Когда задача представлена в виде иерархической структуры, то матрица составляется для парного сравнения критериев на втором уровне по отношению к общей цели, расположенной на первом уровне. Такие же матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня и т. д., если количество уровней больше трех.
Идеальная матрица сравнений – обратно-симметричная и согласованная. При этом справедливо следующее утверждение: положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают, т.е.  .
.
Третий этап. После формирования матриц парных сравнений по всем критериям и
альтернативам необходимо определить собственные векторы матриц, проверить согласованность матриц с помощью их собственных чисел и провести синтез глобальных приоритетов альтернативных решений относительно основной цели.
Для наглядности решения задачи многокритериального выбора используем пример из промышленности: «Выбор электронного оборудования для закупки у производителя ».