Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производную или дифференциал.
Порядком ДУ называется порядок старшей производной, входящей в данное уравнение.
Решением ДУ называется такая функция, которая обращает это уравнение в тождество.
Общим решение ДУ называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решением ДУ называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных.
Дифференциальные уравнения
с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
.
Для решения этого уравнения нужно разделить переменные:
,
а затем проинтегрировать обе части полученного равенства:
.
Примеры
1. Найти общее решение уравнения 
.
Разделив переменные, получим: 
.
Интегрируем обе части равенства:
, 
,
,
,
.
Общим решением будет функция 
.
2. Найти частное решение уравнения 
, удовлетворяющее начальным условиям 
при 
.
Разделим переменные:
.
Проинтегрируем:
,
, 
.
Общим решением будет функция 
.
Для нахождения значения произвольной постоянной с подставим и в общее решение:
, 
, 
.
Следовательно, искомое частное решение имеет вид:
.
Задачи на составление
дифференциальных уравнений
1. Найти закон движения тела по оси ОХ, если оно начало двигаться из точки М (4;0) со скоростью 
.
Решение:
При прямолинейном движении скорость есть производная от пути по времени.
Обозначив путь через х, имеем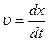 
;
тогда 
, 
.
Интегрируем: 
.
Получим 
.
Используя начальные значения, найдем с.
Так как 
при 
, получим 
.
Итак, закон движения тела имеет вид:
.
2. Составить уравнение кривой, проходящей через точку М (2;-3) и имеющую касательную с угловым коэффициентом 
.
Решение:
Согласно условию, имеем 
, 
; 
, 
.
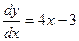Получим 
.
Так как при 
, 
, найдем значение с: 
, 
.
Следовательно, искомое уравнение имеет вид:
.
Простейшие дифференциальные уравнения
второго порядка
Уравнение, содержащее производные (или дифференциалы) не выше второго порядка, называются ДУ второго порядка.
Общее решение ДУ второго порядка имеет две произвольные постоянные.
Пример 1. Найти общее решение уравнения 
.
Это неполное ДУ второго порядка вида 
. Полагаем 
, тогда уравнение примет вид:
, 
.
Интегрируя последнее равенство, получим 
:
, 
.
Следовательно, 
, 
.
Интегрируем и получаем:
,
.
Это и есть общее решение уравнения.
Ответ: .
Пример 2. Найти частное решение уравнения 
, если 
и 
при 
.
Это неполное дифференциальное уравнение второго порядка вида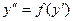 
.
Имеем 
. Разделим переменные 
и проинтегрируем:
, 
, 
.
Имеем 
, 
, 
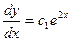, получим общее решение: 
.
Для нахождения частного решения подставим в у и начальные данные:
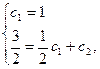
Таким образом, искомое частное решение имеет вид:
.
Ответ: .
Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Линейным однородным ДУ второго порядка с постоянными коэффициентами называется уравнение вида
, (1)
где p и q – постоянные величины.
Для отыскания общего решения составляется характеристическое уравнение
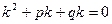, (2)
которое получается из уравнения (1) путем замены 
, и 
на соответствующие степени k, причем сама функция y заменяется единицей.
Общее решение уравнения строится в зависимости от корней 
и 
характеристического уравнения.
Возможны три случая.
1. 
, 
, 
. Уравнение имеет вид:
.
2. 
, 
, 
. Уравнение имеет вид:
.
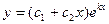3. 
, 
- комплексно-сопряженные числа.
.
Пример 1. Найти частное решение уравнения 
, если 
и при .
Составим характеристическое уравнение и найдем его корни:
, 
, 
.
Так как корни различные и действительные, общее решение запишем в виде:
.
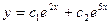Для нахождения частного решения найдем 
и 
. Подставим в общее решение , и получим: 
.
Продифференцируем общее решение 
, подставим в него значение , :
.
Решим систему уравнений:
, 
, 
.
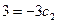Имеем 
, .
Таким образом, получим частное решение:
.
Ответ: .
Пример 2. Найти частное решение уравнения 
, если 
и при .
Составим характеристическое уравнение и найдем его корни:
, 
.
Общее решение уравнения имеет вид:
. (1)
Дифференцируем общее решение:
. (2)
Подставив начальные условия , и в уравнения (1) и (2), получим:
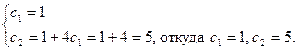
Следовательно, искомое частное решение имеет вид:
.
Ответ: .
Пример 3. Найти частное решение уравнения 
, если при , и 
.
Составим характеристическое уравнение и найдем его корни:
, 
.
Общее решение записываем так:
. (1)
Дифференцируем общее решение:
(2)
Подставив начальные условия в уравнения (1) и (2), получим:
Таким образом, искомое частное решение имеет вид:
.
Ответ: .