Пусть корень уравнения f (х) = 0 отделен на отрезке [ а; b ], причем f ' (х) и f" (х) непрерывны и сохраняют постоянные знаки на всем отрезке [ а; b ]. Геометрический смысл метода Ньютона состоит в том, что дуга кривой у = f (х) заменяется касательной к этой кривой.
Первый случай. Пусть f (а) < 0, f (b) > 0, f ' (х) > 0, f" (х) > 0 (см. рис. 4 (а)) или f (а) > 0, f (b) < 0,
f ' (х) < 0, f" (х) <0 (рис. 4 (б)). Проведем касательную к кривой у = f (х) в точке В0 (b; f (b)) и найдем абсциссу точки пересечения касательной с осью Ох. Известно, что уравнение касательной в точке В0 (b; f (b)) имеет вид
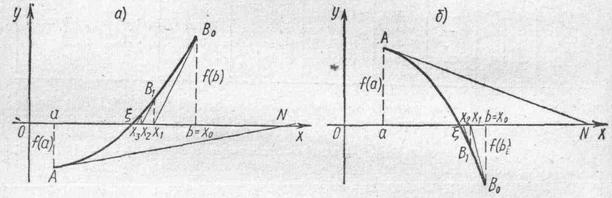
Рис. 4
Полагая у=0, х=х0 , получим
(10)
Теперь корень уравнения находится на отрезке [ а; х1 ]. Применяя снова метод Ньютона, проведем касательную к кривой в точке В1 (х1; f (х1)) и получим
,
и вообще
(11)
Получаем последовательность приближенных значений х1, х2,,…., хп,,.., каждый последующий член которой ближе к корню 
, чем предыдущий. Однако все хп остаются больше истинного корня , т.е. хп— приближенное значение корня с избытком.
Второй случай. Пусть f (а) < 0, f (b) > 0, f ' (х) > 0, f" (х) < 0 (рис. 5(а)) или f (а) > 0, f (b) < 0,
f ' (х) < 0, f" (х) >0 (рис. 5(б)). Если снова провести касательную к кривой у = f (х) в точке В, то она пересечет ось абсцисс в точке, не принадлежащей отрезку [ а; b ]. Поэтому проведем касательную в точке А0 (а; f (а)) и запишем ее уравнение для данного случая:
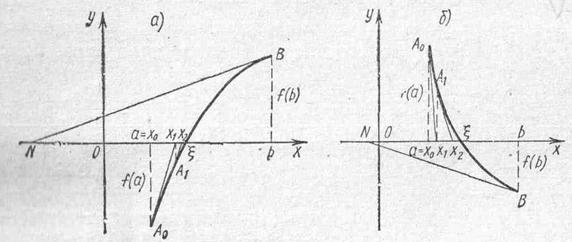
Рис. 5
Полагая у=0, х=х1, находим
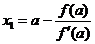(12)
Корень находится теперь на отрезке [ х1 ; b ]. Применяя снова метод Ныотона, проведем касательную в точке
А1 (х1; f (х1) и получим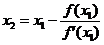 
и вообще (13)
Получаем последовательность приближенных значений х1, х2,,…., хп,,.., каждый последующий член которой ближе к истинному корню , чем предыдущий, т. е. хп — приближенное значение корня с недостатком.
|
|
|
Сравнивая эти формулы с ранее выведенными, замечаем, что они отличаются друг от друга только выбором начального приближения: в первом случае за х0 принимался конец b отрезка, во втором — конец а.
При выборе начального приближения корня необходимо руководствоваться следующим правилом: за исходную точку следует выбирать тот конец отрезка[ а;b ], в котором знак функции совпадает со знаком второй производной. В первом случае f (b) f " (х) > 0 и начальная, точка b= х0, во втором f (а) f "(х) > 0 и в качестве начального приближения берем а = х0.
Рис. 6
Для оценки погрешности можно пользоваться общей формулой
(14)
где 
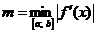(15)
В том случае, когда отрезок [ а, b ] настолько мал, что на нем выполняется условие М2 < 2 т1, где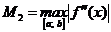 
, а 
, точность приближения на п-м шаге оценивается следующим образом:
если | хп — хп+1 |< 
то | — хп | < 2.
Если производная f ' (х) мало изменяется на отрезке [ а;b ], то для упрощения вычислений можно пользоваться формулой 
, (16)
т. е. значение производной в начальной точке достаточно вычислить только один раз. Геометрически это означает, что касательные в точках Вп (хп; f (хп)) заменяются прямыми, параллельными касательной, проведенной к кривой у= f (х) в точке В0 (х0; f (х0))(см. рис. 6)
Пример 1. Методом касательных уточнить до = 0,001 корень уравнения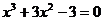 
, расположенный на отрезке [ - 2,75; - 2,5].
Решение: Находим f ' (х) = 3х2 + 6х, f" (х) = 6х + 6. На отрезке [ - 2,75; - 2,5] имеют место неравенства f (- 2,75)<0, f(- 2,75) f" (х) > 0. Поэтому, чтобы воспользоваться методом касательных, следует выбрать х0 =- 2,75. Вычисления будем вести по формуле (16). Находим
|
|
|
f" (-2,75) = 6,1875. Для удобства все вычисления сведем в следующую таблицу:
| n | xn | 
| 
| 3
| 
| 
|
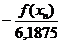
| -2,75 | -20,797 | 7,5625 | 22,6875 | -1,111 | 0,179 | |
| -2,571 | -16,994 | 6,6100 | 19,8300 | -0,164 | 0,026 |
149
| -2,545 | -16,484 | 6,4770 | 19,431 | -0,053 | 0,008 | |
| -2,537 | -16,329 | 6,43646 | 19,309 | 0,020 | 0,003 | |
| -2,534 | -16,271 | 6,4212 | 19,2636 | 0,007 | 0,001 | |
| -2,533 |
Из таблицы видно, что | х5 — х4 |< 0,001, поэтому корень = - 2,533.
Задание
Вариант 1
1. Дано уравнение 
.
а) Отделить корни данного уравнения, пользуясь аналитическим методом;
б) методом половинного деления уточнить один корень уравнения с точностью 10-3;
2. Дано уравнение 
.
а) Отделить корни данного уравнения, пользуясь аналитическим методом;
б) методом касательных уточнить один корень уравнения с точностью 10-3;
Вариант 2
1. Дано уравнение 
.
а) Отделите корни уравнения, пользуясь аналитическим методом;
б) методом половинного деления уточнить один корень данного уравнения с точностью 10-3;
2. Дано уравнение 
.
а) Отделить корни данного уравнения, пользуясь аналитическим методом;
б) методом касательных уточнить один корень данного уравнения с точностью 10-3;
Вариант 3
1. Дано уравнение 
.
а) Отделить корни уравнения, пользуясь аналитическим методом;
б) методом половинного деления уточнить один корень данного уравнения с точностью 10-3;
2. Дано уравнение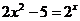 
.
а) Отделить корни данного уравнения, пользуясь аналитическим методом;
|
|
|
б) методом касательных уточнить один корень данного уравнения с точностью 10-3;
Вариант 4
1. Дано уравнение 
.
а) Отделить корни уравнения, пользуясь аналитическим методом;
б) методом половинного деления уточнить один корень данного уравнения с точностью 10-3;
2. Дано уравнение 
.
а) Отделить корни данного уравнения, пользуясь аналитическим методом;
б) методом касательных уточнить один корень данного уравнения с точностью 10-3;
4. Контрольные вопросы:
1. Какие уравнения называются алгебраическими? Трансцентдентными?
2. Что значит решить уравнение? Какие этапы включает в себя решение уравнение?
3. Какие методы для отделения корней вы знаете?
4. Назовите методы уточнения корней и формулы, которые в них применяются.
5. Содержание отчёта:
5.1 Наименование работы
5.2 Цель работы
5.3 Задание
5.4 Формулы для расчета
5.5 Необходимые расчеты. Анализ результатов расчетов
5.6 Выводы по работе
5.7 Ответы на контрольные вопросы
6. Литература:
1. Лапчик М.П., Рагулина М.И., Хеннер Е.К., Элементы численных методов: учебник для студ.
сред проф. образования. - М.: Издательский центр «Академия», 2007, с.49-56, 67-73.
