Электрическая схема.
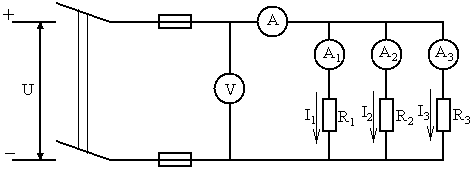
Ход работы.
Основные теоретические положения
В данной работе исследуется электрическая цепь, состоящая из трех резисторов при их последовательном, параллельном и смешанном соединениях.
При последовательном соединении сопротивлений (рис. 1.1, а) общее сопротивление цепи равно сумме сопротивлений, входящих в состав цепи, т. е.
.
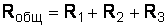При параллельном соединении сопротивлений (рис. 1.1, б) общая проводимость цепи равна сумме проводимостей отдельных ее ветвей:
,
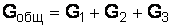где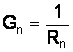 
– проводимость соответствующего участка электрической цепи, См (Сименс).
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
,
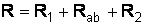где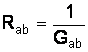 
; 
.
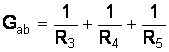а б в
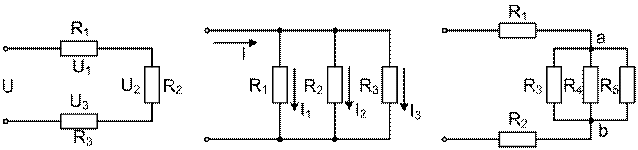
Рис1. Электрические цепи соединения сопротивлений: а – последовательное; б – параллельное; в – смешанное
Закон Ома устанавливает связь между током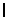 
и напряжением 
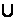на некотором участке цепи. Ток в проводнике прямо пропорционален напряжению между концами проводника и обратно пропорционален сопротивлению этого же проводника, т. е. 
.
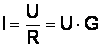1-й закон Кирхгофа. Алгебраическая сумма токов, подтекающих к любому узлу разветвленной электрической цепи, равна нулю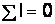 
, или сумма подтекающих к любому узлу токов равна сумме оттекающих от узла токов (рис. 2.1, б): 
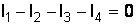, или 
.
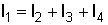2-й закон. Алгебраическая сумма падений напряжений в любом замкнутом контуре электрической цепи равна алгебраической сумме эдс вдоль того же контура (рис. 2.1, а), т. е.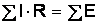 
, или алгебраическая сумма напряжений (не падений напряжений) вдоль любого замкнутого контура равна нулю, т. е. 
: 
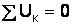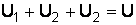, или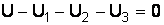 
.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
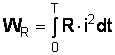, при 
; 
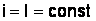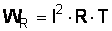, Дж;
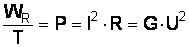, Вт, – мощность нагрузки.
Баланс мощностей (закон сохранения энергии в электрической цепи).
Суммарная мощность источников электрической энергии 
равна общей мощности, поглощаемой сопротивлениями нагрузки (потребителями) 
, входящими в состав цепи, т. е.
= 
.
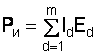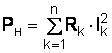Относительная ошибка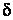 
должна быть меньше наперед заданного числа, например 5 %:
.
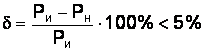| U | U1 | U2 | U3 | I1 | I2 | I3 | I | Р | Р1 | Р2 | Р3 | R | R2 | R3 | R |
| В | В | В | В | А | А | А | А | Вт | Вт | Вт | Вт | Ом | Ом | Ом | Ом |
| 1,0 | 0,2 | 0,4 | 1,63 | ||||||||||||
| 34,5 | 0,7 | 0,3 | 0,5 | 1,51 |
Включим цепь и произведем измерение величин.
1.I = I1 + I2 + I3
2.U = U1 = U2 = U3
3.P = U×I
4.R = U/I
В отчет включаем всё, что синим цветом.
· Записываем данные в таблицу, рассчитываем мощности и сопротивления на всех участках (согласно формул 3 и 4).
· Отвечаем на контрольные вопросы (письменно, вопросы можно не записывать- только ответы) Это обязательно!
· Делаем вывод к работе (по цели)
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
1 Почему при последовательном соединении резисторов величина силы тока на всех
элементах в цепи имеет одинаковые значения?
2.Почему при параллельном соединении резисторов разность потенциалов на всех
элементах цепи имеет одинаковое значение?
3 Если несколько резисторов с разными по величине значениями сопротивлений
соединить последовательно, то на каком из них будет большее падение напряжения?
4 Если несколько резисторов с разными по величине значениями сопротивлений
соединить последовательно, то на каком из них будет больший ток?
5 Как определить проводимость ветвей и эквивалентную проводимость цепи при
параллельном соединении резисторов?
6 Как определить эквивалентную проводимость цепи при последовательном соединении
7 Укажите все возможные расчетные формулы для определения мощности резисторов.