Расчет трехфазной цепи при соединении симметричной нагрузки звездой.

АНАЛИЗ ТРЕХФАЗНЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

 

Автор курсовой работы

Специальность 210102 «Светотехника и источники света»

Обозначение курсовой работы КР–02069964–210102-0–12

Руководитель работы В.М. Каликанов

 

Оценка

 

Саранск 2012

 

МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н. П. ОГАРЕВА

Факультет светотехнический

Кафедра ТОЭ

 

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Студент:

1 Тема: Расчет трехфазных цепей переменного синусоидального тока

2 Исходные данные для научного исследования (проектирования)

 

R_a=R_b=R_с=20 Ом

L_a=L_b=L_c=70 мкГ

С_а=С_b=С_с=600 мкФ

е = l00Sinωt

 

 

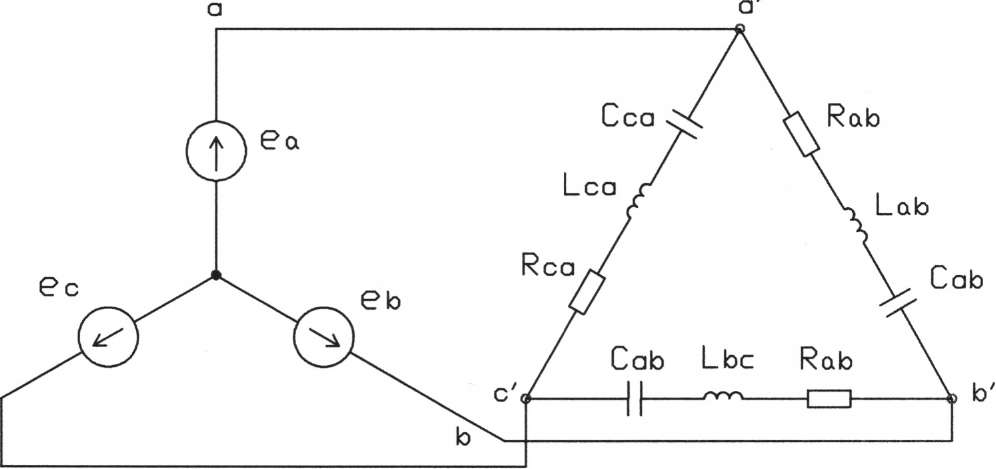
Рис 1. Схема трехфазной цепи при соединении нагрузки звездой

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12

Разраб.

Провер.

Каликанов В.М. ВввВ.М.В.М.

Реценз.

Н. Контр.

Утверд.

Курсовая работа

Лит.

Листов

МГУ, СТФ, Сервис

 

Рис 2. Схема трехфазной цепи при соединении симметричной нагрузки звездой

 

 

Руководитель работы ____________В.М. Каликанов

Задание принял к исполнению ____________

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12

Содержание

Введение.............................................................................................................. 5

1. Расчет трехфазной цепи при соединении симметричной нагрузки звездой. 6

2. Расчет трехфазной цепи при соединении симметричной нагрузки

тругольником................................................................................................... 11

Заключение........................................................................................................ 16

КР-02069964-210102-0-12

Лист

Дата

Подпись

№ докум.

Лист

Изм.

Список используемых источников............................................................... 17

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12

Введение

 

Трехфазная цепь является частным случаем многофазных систем электрических цепей, представляющих собой совокупность электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и создаваемые общим источником энергии.

Трехфазные цепи наиболее распространенные в современной электроэнергетике. Это объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями:

- экономичность производства и передачи энергии по сравнению с однофазными цепями;

- возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя;

- возможность получения в одной установке двух эксплуатационных напряжений - фазного и линейного.

Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.

Все методы расчета разделяются на две группы

1. Расчет по мгновенным значениям.

2. Расчет по действующим значениям токов и напряжений.

При расчете по мгновенным значениям составляются уравнения по законам Кирхгофа для мгновенных значений. При этом получается система дифференциальных уравнений. Рассчитывая мгновенные значения токов и напряжений для отдельных моментов времени, отстающих друг от друга на временной интервал Δt получаем зависимости i(t) u (t). Такой расчет будет называться - расчет во вре­менной области.

При расчете по действующим значениям сводят форму напряжений и токов к синусоидальной. Выражают синусоидальную величину в комплексном виде, получается алгебраическая система уравнений которая решается через определители.

Наиболее часто применяется расчет по действующим значениям тока и напряжений методом комплексных амплитуд (символический метод)

 

 

Расчет трехфазной цепи при соединении симметричной нагрузки звездой.

1.1. Определяем индуктивное и емкостное сопротивление.

Х_LА =Х_LB = Х_LС = ωL_А = 314 ּ70ּ10^-3 =22 Ом

Х_CA=Х_СА = Х_СC= =5 Ом

 

1.2. Рассчитаем полное сопротивление фаз нагрузки.

Z_A =Z_B=Z_C = = 20² + (22 - 5)² = 26 Ом

 

1.3 Найдем фазное напряжение

е_А= U_A = Е_mSin ωt = 1 00Sinωt В

е_н = U_B = Е_mSin(ωt -120°) = 1 00Sin(ωt - 120°) В

е_C =U_C= Е_mSin(ωt +120°) = 100 Sin(ωt + 120°) В

1.4. Определим угол сдвига фаз между токами и фазными напряжениями.

tgφ_A = tgφ_В = tgφ_С =

φ_A= φ_B= φ_{C =} 41°

1.5 Рассчитаем ток.

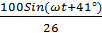= = 3,8Sin()A

= = 3,8Sin()A

= 3,8Sin()A

1.6. Рассчитаем падение напряжения на элементах фазы А

U_RA =I_AR_A= 3,8 Sin(ωt + 41°) 20 = 76Sin(ωt + 41 ) В

U_LA = I_АX_LA = 3,8 Sin(ωt + 41°) 22(+90 ) = 84Sin(ωt + 131°) В

U_CA = I_AX_CA = 3,8 Sin(ωt + 41°) 5(-90 ) = 19Sin(ωt -49 ) В

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12

1.7. Рассчитаем падение напряжения на элементах фазы В

U_RB = I_B •R_B =3.8Sin( ωt-120° + 41°) • 20 = 76Sin( ωt - 79⁰) В

U_LB =I_B • X_LB = 3.8 Sin (ωt-120° + 41") • 22(+90⁰) = 84Sin( ωt+11°)

U_CB =I_B • X_LB = 3.(ωt-120° + 41 °) • 5(-90⁰) = 19 Sint (ωt-169°)В

1.8. Рассчитаем падение напряжения на элементах фазы С

U_RC = I_C • R_C = 3.8Sin + 120"+41 °) • 20 = 76Sin (ωt+ 161°) В

U_LC =1_С • Х_LC = 3.8Sin+120° + 41°) • 22(+90°) = 84Sin (ωt+ 251") В

U_CC = 1_С • Х_CC = 3.8Sin +120° + 41°) • 5(-90°) = 19 Sin( ωt+ 71") В

1.9. Найдем линейные напряжения.

U _ab = U_а • (+30°) = 100 • 1,73 = 1 73Sin( ωt + 30°) В

U_bc = U _b • (-90°) = 173 Sin( ωt- 90°) В

U_ca =U_c • (+150°) = 173 Sin (ωt+ 150°) B

Рассчитаем баланс мощностей

1.10. Полная мощность, которую выделяет ЭДС.

S_E =E_A • I_A+E_B • I_B+E_C • I_C =3E_A • I_A =3•100•3,8 = 1140 Ва

1.11. Активная мощность.

P_R = • R_A + • R_B + • R_C = R_A = 3,8² • 20 = 289 Вт

1.12 реактивная мощность.

Q _LC= • X_LA + •X_LB + • X_LC- • X_CA - •X_CB - •X_CC = – X_LA - • X_CA = 3-3,8² -22-3-3,8² -5 = 736 Вар

КР-02069964-210102-0-12

Лист

Дата

Подпись

№ докум.

Лист

Изм.

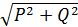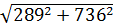S= = = 791 Вa

 

 

 

Рисунок 1. Диаграмма токов

 

 

КР-02069964-210102-0-12

Лист

Дата

Подпись

№ докум.

Лист

Изм.

 

 

Рисунок 2. Диаграмма литейных и фазных напряжений

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12

 

Рисунок 3. Диаграмма фазных напряжений на элементах нагрузки

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-02069964-210102-0-12