Часть 6. Арифметическое векторное пространство
Базисы арифметических пространств. Связь между координатами вектора в различных базисах
Определение. Множество матриц (столбцов) размерности n x 1 с линейными операции над ними называется n - мерным арифметическим векторным пространством размерности n и обозначается символом R 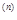 .
.
Базисы (1); 

 ...;
...;  называются естественными базисами векторных пространств R
называются естественными базисами векторных пространств R 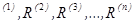 соответственно. Разложение произвольного вектора
соответственно. Разложение произвольного вектора  по базису в пространстве
по базису в пространстве  имеет вид
имеет вид  , в котором первые сомножители – это действительные числа (координаты вектора), а вторые сомножители – это соответствующие базисные векторы.
, в котором первые сомножители – это действительные числа (координаты вектора), а вторые сомножители – это соответствующие базисные векторы.
Для сокращения записей рассматрим этот вопрос для пространства  . Пусть
. Пусть  – координаты вектора
– координаты вектора  в базисе
в базисе 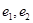 и
и  – координаты этого же вектора в базисе
– координаты этого же вектора в базисе  ,
, 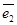 и пусть
и пусть
 =
= 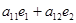 ,
, 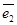 =
= 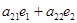
или иначе:
 ,
,
где
 -
-
матрица координат векторов «нового» базиса в «старом» базисе (матрица перехода от одного базиса к другому). Тогда
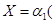
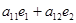 ) +
) +  (
(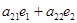 ) = =(
) = =( .
.
Так как координаты вектора в одном и том же базисе определяются однозначно, то
( .
.
В матричной форме это имеет вид:
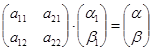 . Т.е.
. Т.е.  .
.
Отсюда следует, что:
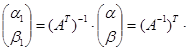 .
. 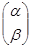 .
.
Пример.  в декартовом базисе
в декартовом базисе  Найти координаты вектора
Найти координаты вектора 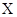 в базисе
в базисе 
Решение.


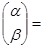 (
( .
.
Ясно, что не всякие векторы образуют базис в пространстве  . Выяснить эту возможность помогает следующая теорема.
. Выяснить эту возможность помогает следующая теорема.
Теорема 6.1. Множество n векторов образует базис в пространстве  тогда и только тогда, когда определитель
тогда и только тогда, когда определитель  матрицы А, составленной из его координат, не равен нулю.
матрицы А, составленной из его координат, не равен нулю.
Доказательство. Пусть векторы

 , …,
, …, 
образуют базис в пространстве  , тогда они образуют линейно независимое множество и поэтому
, тогда они образуют линейно независимое множество и поэтому


и, следовательно, 
Если  , то среди столбцов матрицы А нет линейно зависимых и поэтому векторы
, то среди столбцов матрицы А нет линейно зависимых и поэтому векторы  ,
,  образуют базис в пространстве
образуют базис в пространстве  .
.
Теорема доказана.
Пример. Доказать, что векторы
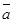 =
=  ,
,  =
= 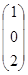 ,
,  =
= 
образуют базис и найти координаты вектора  =
= 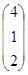 в этом базисе.
в этом базисе.
Решение. Так как определитель
 =
=  = 0 + 0 +4 -0 -1 -6 =-3
= 0 + 0 +4 -0 -1 -6 =-3  ,
,
то векторы 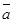 ,
,  ,
,  образуют базис в пространстве
образуют базис в пространстве  . Для нахождения координат вектора
. Для нахождения координат вектора  решаем уравнение
решаем уравнение  = k
= k 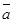 + m
+ m  + n
+ n  , которое равносильно системе уравнений
, которое равносильно системе уравнений

Так как определитель этой системы отличен от нуля, то применяем для ее решения формулы Крамера.
 = -3,
= -3, 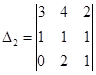 = -3,
= -3,  = 0,
= 0,
 .
.
Следовательно,
 =
= 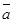 +
+  + 0
+ 0 
и (1; 1; 0) – координаты вектора  в базисе {
в базисе {  ,
,  ,
,  }.
}.
Подпространства и линейные оболочки
Определение. Пусть S – некоторое подмножество векторного пространства  . Если S является векторным пространством с теми же линейными операциями, что и в
. Если S является векторным пространством с теми же линейными операциями, что и в  , то S называется векторным подпространством пространства
, то S называется векторным подпространством пространства  .
.
Нуль – вектор всегда является подпространством в  . Размерность k подпространства меньше или равна размерности
. Размерность k подпространства меньше или равна размерности  . Так что S =
. Так что S = 
 , где
, где  Для получения подпространства размерности k достаточно взять множество любых k линейно независимых векторов из
Для получения подпространства размерности k достаточно взять множество любых k линейно независимых векторов из  и составить всевозможные линейные комбинации из них. Полученное таким образом подпространство называется линейной оболочкой этого множества векторов. Линейная оболочка одного вектора совпадает с пространством
и составить всевозможные линейные комбинации из них. Полученное таким образом подпространство называется линейной оболочкой этого множества векторов. Линейная оболочка одного вектора совпадает с пространством  ; линейная оболочка двух линейно независимых векторов совпадает с пространством
; линейная оболочка двух линейно независимых векторов совпадает с пространством 
и т.д.
Определение. Суммой двух подпространств S  и S
и S  из пространства
из пространства  называется множество всех векторов вида
называется множество всех векторов вида 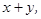 где
где  .
.
Теорема 6. 2. Сумма 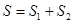 подпространств
подпространств  является подпространством.
является подпространством.
Доказательство. Пусть
 .
.
Тогда


потому что
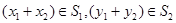 .
.
Далее, пусть  - любое число. Тогда
- любое число. Тогда
 ,
,
так как  .
.
Теорема доказана.
Примеры.
1. Если  – подпространства, представляющие собой две различные прямые, проходящие через начало координат трех мерной декартовой системы координат, то
– подпространства, представляющие собой две различные прямые, проходящие через начало координат трех мерной декартовой системы координат, то 
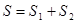 - это плоскость, содержащая эти прямые.
- это плоскость, содержащая эти прямые.
2. Если  – подпространства, представляющие собой две различные плоскости, проходящие через начало координат трех мерной декартовой системы координат, то
– подпространства, представляющие собой две различные плоскости, проходящие через начало координат трех мерной декартовой системы координат, то 
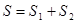 - все трех мерное пространство.
- все трех мерное пространство.
Определение. Пересечением двух подпространств S1 и S2 из пространства  называется множество всех векторов, принадлежащихS
называется множество всех векторов, принадлежащихS  и S
и S  , пишут
, пишут  .
.
Теорема 6.3. Сумма и пересечение подпространств из  являются подпространствами
являются подпространствами  относительно тех же линейных операций, что и в
относительно тех же линейных операций, что и в  .
.
Доказательство этой теоремы очевидно и предоставляется читателю.
Определение. Сумма подпространств 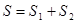 называется прямой суммой, если
называется прямой суммой, если  - пустое множество, т.е. содержит только нуль-вектор. В этом случае пишут
- пустое множество, т.е. содержит только нуль-вектор. В этом случае пишут  .
.