Метод Жордана-Гаусса
Алгоритм метода:
1) выбирают в системе уравнений одно уравнение и называют его ведущим;
2) в этом уравнении выбирают одну неизвестную, коэффициент у которой отличен от нуля, и называют ее ведущей;
3) подбирают числовые множители для каждого из уравнений с таким расчетом, чтобы после сложения ведущего уравнения с каждым из других уравнений системы в них «пропала» ведущая неизвестная;
4) выбирают другое уравнение и другую неизвестную системы в качестве ведущих и выполняют пункт 3.
Осуществляя такие действия необходимое количество раз, приходят к системе, в которой в каждом уравнении содержится точно по одной неизвестной, если система имеет единственное решение. Если система имеет "лишние" неизвестные, то их переносят в правую сторону уравнений и через них выражают остальные неизвестные. Если система противоречива, то противоречие становится очевидным на каком-то шаге применения алгоритма.
Пример. Решить систему уравнений:
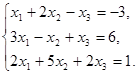
Решение. Первое уравнение и неизвестную х1 считаем ведущими. Умножая первое уравнение на (-3) и на (-2) и последовательно складывая его со вторым и третьим уравнениями, приходим к системе:

Решение. Первое уравнение и неизвестную х1 считаем ведущими. Умножая первое уравнение на (-3) и на (-2) и последовательно складывая его со вторым и третьим уравнениями, приходим к системе:

Выбираем третье уравнение и неизвестную х2 в качестве ведущих. Умножая третье уравнение на (-2) и на (7) и складывая его последовательно с первым и вторым уравнениями, получим систему:

Второе уравнение сократим на 32. Получим систему:

Выбираем в качестве ведущих второе уравнение и неизвестную х 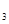 . Умножаем второе уравнение на 9 и складываем с первым уравнением. Умножаем второе уравнение на (-4) и складываем с третьим уравнением. Получим систему:
. Умножаем второе уравнение на 9 и складываем с первым уравнением. Умножаем второе уравнение на (-4) и складываем с третьим уравнением. Получим систему:

Таким образом, неизвестные системы найдены.
Вычисление коэффициентов при решении системы уравнений методом Жордана-Гаусса с помощью правила прямоугольника
Пусть: a – коэффициент при разрешающей неизвестной; b – коэффициент при другой неизвестной в разрешающем уравнении, или свободный коэффициент этого уравнения; с, d – соответствующие им коэффициенты в другом уравнении системы. Тогда на каждом шаге преобразования системы методом Жордана–Гаусса можно вычислять коэффициенты, используя следующее правило:
в последующей системе коэффициенты a, b сохраняются, коэффициент c переходит в ноль, коэффициент d переходит в (ad – bc).
Так как система уравнений однозначно определяется матрицей ее коэффициентов, то вместо преобразования уравнений можно делать соответствующие преобразования матриц ее коэффициентов.
Пример. Решить систему уравнений:

Решение.
 –
–  --
--
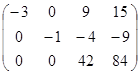 –
–  –
–
 –
–  .
.
Таким образом, 
Метод обратной матрицы
Если система имеет вид: АХ = В, где А квадратная матрица с ненулевым определителем, то Х = А-1В. Таким образом, чтобы найти матрицу неизвестных системы уравнений, надо найти обратную матрицу и умножить ее на матрицу свободных коэффициентов системы.
Пример.
Решить систему уравнений

Решение.
А= 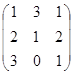 ,
, 
 ,
,

Таким образом: x1 = 2, x2 = 1, x3 = 2.
Однородные системы
Определение. Система линейных уравнений называется однородной, если все ее свободные коэффициенты равны нулю.
Однородная система имеет вид:

Ясно, что любая однородная система совместна, так как она имеет по крайней мере нулевое решение (0; 0; 0;…,0). Ранг ее основной матрицы равен рангу расширенной матрицы, так как последняя содержит дополнительный столбец, состоящий из нулей., который не увеличивает ранга матрицы системы. Если количество уравнений системы совпадает с рангом матрицы системы и количеством неизвестных (r = m = n), то нулевое решение будет единственным ее решением (это легко видеть из процедуры решения системы методом Крамера). Если r = m < n, то система состоит из линейно независимых уравнений, в которой (n – r) свободных неизвестных (в том смысле, что им можно задавать любые значения), и поэтому она имеет бесконечное множество решений. Если определитель матрицы квадратной системы равен нулю, то она имеет бесчисленное множество решений, потому что в этом случае выполняется неравенство r < n и система будет иметь (n – r)  0 свободных неизвестных.
0 свободных неизвестных.
Пример. Решить систему уравнений

Решение. Решаем систему методом Жордана–Гаусса.




Таким образом,  , где t – любое число.
, где t – любое число.
Cвойства решений однородной системы уравнений
1. Если ( – решение однородной системы и d – любое число, то (
– решение однородной системы и d – любое число, то ( – решение этой системы.
– решение этой системы.
2. Если ( и (
и ( – два решения однородной системы, то (
– два решения однородной системы, то ( – решение этой системы.
– решение этой системы.
3. Если ( и (
и ( – два решения однородной системы d,k – любые числа, то (
– два решения однородной системы d,k – любые числа, то (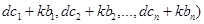 − решение этой системы.
− решение этой системы.
Доказательство. Третье свойство обобщает первые два свойства. Проверим его непосредственно подстановкой в i - е уравнение системы.



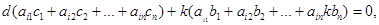
 ,
, 
Свойства доказаны.