Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается
называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается  или
или  .
.
Итак, по определению
 =
=  , где
, где 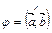 .
.
Если  = (
= ( ),
),  = (
= ( ), то
), то
 =
=  .
.
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 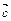 , который:
, который:
1.перпендикулярен векторам  и
и  ;
;
2. имеет длину 
 , где
, где 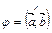 .
.
3. векторы 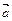 ,
, 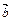 и
и  образуют правую тройку.
образуют правую тройку. 
Векторное произведение обозначается 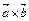 или
или 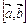 .
.
Если 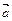 =(
=( ),
), 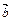 = (
= ( ), то
), то
 .
.
Вектор 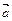 коллинеарен вектору
коллинеарен вектору 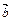 тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие  =0.
=0.
Площадь треугольника, построенного на векторах  и
и  будет равна
будет равна  .
.
Произведение  векторов
векторов 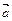 ,
, 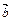 и
и  называется смешанным. Смешанное произведение представляет собой некоторое число. Так как смешанное произведение не меняется при перемене местами знаков векторного и скалярного произведения, то его принято записывать
называется смешанным. Смешанное произведение представляет собой некоторое число. Так как смешанное произведение не меняется при перемене местами знаков векторного и скалярного произведения, то его принято записывать 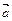
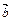
 .
.
Векторы 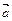 ,
, 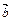 и
и  компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда 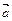
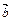
 =0.
=0.
Если 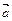 = (
= (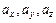 ),
), 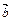 = (
= ( ),
),  = (
= ( ), то
), то


 =
=  .
.
Пример 1. Определить угол между векторами  .
.
Решение. Так как 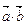 =
= 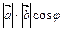 , то
, то  . Имеем
. Имеем 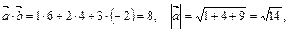
 .
.
Следовательно,  и
и  .
.
Пример 2. Вычислить площадь Δ АВС, если А(1;1;1), В(2;3;4), С(4;3;2).
Решение. Найдем координаты векторов  . Получим
. Получим  . Вычислим векторное произведение данных векторов.
. Вычислим векторное произведение данных векторов.
 . Следовательно
. Следовательно  (кв.ед.).
(кв.ед.).
Пример 3. Найти объем треугольной пирамиды с вершинами А(2;2;2), В(4;3;3), С(4;5;4) и D(5;5;6).
Решение. Найдем координаты векторов  , совпадающие с ребрами пирамиды, сходящимися в вершине А. Получим
, совпадающие с ребрами пирамиды, сходящимися в вершине А. Получим  . Вычислим смешанное произведение
. Вычислим смешанное произведение
 этих векторов:
этих векторов:  . Тогда
. Тогда  (куб.ед.).
(куб.ед.).
Упражнения:
1. Пусть 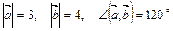 . Вычислить:
. Вычислить:
а)  ; б)
; б)  .
.
2. Даны векторы  . Вычислить
. Вычислить
а)  ; б)
; б) 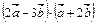 ; в)
; в)  ; г)
; г)  .
.
3. Найти векторное произведение векторов 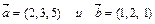 .
.
4. Даны векторы:
а)  ; б)
; б)  .
.
Найти координаты вектора  .
.
5. Вычислить площадь параллелограмма, построенного на векторах  .
.
6. Вычислить площадь Δ АВС, если А(2;2;2), В(4;0;3), С(0;1;0).
7. Показать, что векторы
 компланарны.
компланарны.
8. Найти объем треугольной пирамиды с вершинами А(0;0;1), В(2;3;5), С(6;2;3) и D(3;7;2). Найти длину высоты пирамиды, опущенной на грань ВСD.
9. Показать, что точки А(5;7;-2), В(3;1;-1), С(9;4;-4) и D(1;5;0) лежат в одной плоскости.
Прямая на плоскости
Уравнение
Ах + Ву + С = 0 (1)
(где А,В и С – постоянные коэффициенты, причем А2 + В2¹ 0) определяет на плоскости прямую. Это уравнение называется общим уравнением прямой.

 Если в общем уравнении прямой В ¹ 0, то, разрешив его относительно у, получим уравнение вида
Если в общем уравнении прямой В ¹ 0, то, разрешив его относительно у, получим уравнение вида
y = kx + b (2)
(здесь  ). Его называют уравнением прямой с угловым коэффициентом, поскольку
). Его называют уравнением прямой с угловым коэффициентом, поскольку  , где α – угол, образованный прямой с положительным направлением оси Ох.
, где α – угол, образованный прямой с положительным направлением оси Ох.
Если в общем уравнении прямой С ¹ 0, то, разделив все его члены на –С, получим уравнение вида
 (3)
(3)
(здесь  ). Его называют уравнением прямой в отрезках.
). Его называют уравнением прямой в отрезках.
Острый угол между прямыми y = k1 x + b1 и y = k2 x + b2 определяется по формуле
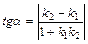 . (4)
. (4)
Условие параллельности прямых имеет вид k1 = k2.
Условие перпендикулярности прямых имеет вид k1k2 = -1.
Уравнение прямой, проходящей через точки М1(х1,у1) и М2(х2,у2), записывается в виде
 . (5)
. (5)
Если х1 = х2, то уравнение прямой имеет вид х = х1. Если у1 = у2, то уравнение прямой имеет вид у = у1.
Расстояние от точки М(х0,у0) до прямой Ах + Ву + С = 0 находится по формуле
 . (6)
. (6)
Пример 1. Через точку М(2;-1) провести прямую, параллельную прямой 4 х -7 у +12=0.
Решение. Запишем уравнение данной прямой в виде уравнения с угловым коэффициентом  . Т.к. прямая, проходящая через точку М должна быть параллельна исходной прямой, то ее угловой коэффициент должен быть равен
. Т.к. прямая, проходящая через точку М должна быть параллельна исходной прямой, то ее угловой коэффициент должен быть равен 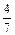 . Поэтому ее уравнение будет иметь вид
. Поэтому ее уравнение будет иметь вид  . Для нахождения значения в подставим координаты точки М. Получим
. Для нахождения значения в подставим координаты точки М. Получим  . Отсюда
. Отсюда  . Таким образом, получаем уравнение
. Таким образом, получаем уравнение  .
.
Пример 2. Даны вершины треугольника: А(4;6), В(-4;0) и С(-1;-4). 1) Составить уравнения: а) стороны АВ; б) медианы, проведенной из вершины С. 2) найти длину высоты, проведенной из вершины С.
Решение. 1а) Полагая х1=4, у1=6, х2=-4, у2=0 в уравнении (5) получаем
 , или
, или 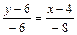 .
.
Отсюда искомое уравнение имеет вид 3 х -4 у +12=0.
1б) Найдем координаты середины стороны АВ:
 .
.
Воспользуясь уравнением (5), получим уравнение медианы 7 х - у +3=0.
2) Найдем длину высоты СС1 как расстояние от точки С до прямой АВ по формуле (6). Получим
 .
.
Упражнения:
1. Построить прямые: а) х -2 у +5=0; б) 2 х +3 у =0; в) 5 х -2=0; г) 2 у +7=0.
2. Дано общее уравнение прямой 12 х -5 у -65=0. Написать: а) уравнение с угловым коэффициентом; б) уравнение в отрезках.
3. Написать уравнение прямой, которая проходит через начала координат и:
а) параллельна прямой у=4 х -3;
б) образует угол в 45° с прямой у=2 х +5;
в) перпендикулярна прямой у=  ;
;
г) образует угол в 60° с прямой у= х -1.
4. Даны вершины треугольника А(2;2), В(-2;-8) и С(-6;-2). Составить уравнения медиан треугольника.
5. Найти расстояние точки М0:
а) М0(4;-2) от прямой 8 х -15 у -11=0;
б) М0(2;7) от прямой 12 х +5 у -7=0;
в) М0(-3;5) от прямой 9 х -12 у +2=0.
6. Даны вершины треугольника А(0;2), В(7;3) и С(1;6). Определить 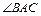 .
.
7. При каком значении т прямые 7 х -2 у -5=0, х +7 у -8=0, тх + ту -8=0 пересекаются в одной точке.
Кривые второго порядка
Уравнение
Ах2 + Су2 +2Dх + 2Еу + F =0, (1)
где коэффициенты А и С не равны нулю одновременно, определяет либо окружность (при А = С), либо эллипс (при А×С >0), либо гиперболу (при А×С< 0), либо параболу (при А×С= 0). При этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.
Окружность – это множество всех точек плоскости, равноудаленных от данной точки (центра). Если r – радиус окружности, а точка С(а;b) – ее центр, то уравнение окружности имеет вид (рис. 1)
 . (2)
. (2)
В частности, если центр окружности совпадает с началом координат, то последнее уравнение примет вид (рис. 2)
 . (3)
. (3)
 |  | ||
рис.1 рис.2
Эллипсом называется множество всех точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная больше расстояния между фокусами.
Если точка С(х0;у0) – центр эллипса, то его уравнение имеет вид (рис. 3)
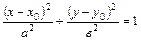 , (4)
, (4)
где а – большая, в - малая полуось эллипса, причем  (с – половина расстояния между фокусами).
(с – половина расстояния между фокусами).
В частности, если центр эллипса совпадает с началом координат, то последнее уравнение имеет вид (рис. 4)

 . (5)
. (5)
 |
рис.3 рис. 4
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами.
Если точка С(х0;у0) – центр гиперболы, то ее уравнение имеет вид (рис. 5)
 , (6)
, (6)
причем  .
.
В частности, если центр гиперболы совпадает с началом координат, то последнее уравнение имеет вид (рис. 6)
 . (7)
. (7)
 | |||
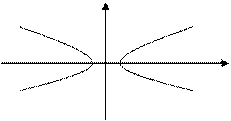 | |||
рис.5 рис.6
Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая  , а фокусом – точка
, а фокусом – точка  , то уравнение параболы имеет вид
, то уравнение параболы имеет вид
 . (8)
. (8)
Эта парабола расположена симметрично относительно оси абсцисс (рис. 7).
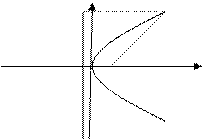 |
р ис.7
Пример 1. Найти координаты центра и радиус окружности 2 х2 + 2 у2 - - 8 х + 5 у - 4 = 0.
Решение. Разделив уравнение на 2 и, сгруппировав члены уравнения, получим  . Дополним выражения
. Дополним выражения  и
и  до полных квадратов, прибавив к первому двучлену 4 и ко второму
до полных квадратов, прибавив к первому двучлену 4 и ко второму  (одновременно к правой части прибавляется сумма этих чисел):
(одновременно к правой части прибавляется сумма этих чисел):
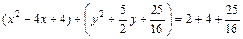 ,
,
или
 .
.
Таким образом, координаты центра окружности  , а радиус окружности
, а радиус окружности 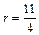 .
.
Пример 2. Установить вид кривой второго порядка, заданной уравнением 4 х2 + 9 у2 - 8 х - 36 у + 4 = 0.
Решение. Преобразуем данное уравнение следующим образом:

Отсюда 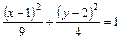 . Таким образом, заданная кривая является эллипсом.
. Таким образом, заданная кривая является эллипсом.
Пример 3. Написать каноническое уравнение гиперболы, зная, что расстояние между фокусами 2 с = 10, а между вершинами 2 а = 8.
Решение. Из условия  получаем в = 3. Тогда уравнение гиперболы примет вид
получаем в = 3. Тогда уравнение гиперболы примет вид  .
.
Пример 4. Гипербола симметрична относительно осей координат, проходит через точку М (6;  ) и имеет мнимую полуось в = 2. Написать уравнение и найти расстояние точки М от фокусов.
) и имеет мнимую полуось в = 2. Написать уравнение и найти расстояние точки М от фокусов.
Решение. В уравнение 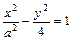 подставим координаты точки М. Получим
подставим координаты точки М. Получим  . Отсюда
. Отсюда  . Тогда уравнение гиперболы имеет вид
. Тогда уравнение гиперболы имеет вид  .
.
Из условия  получаем
получаем  т.е.
т.е. 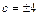 . Следовательно, фокусы имеют координаты
. Следовательно, фокусы имеют координаты  .
.
Тогда  ,
,  .
.
Упражнения:
1. Установить, что каждое из следующих уравнений определяет окружность, найти ее центр С и радиус r:
а)  ; г)
; г)  ;
;
б)  ; д)
; д) 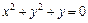 ;
;
в)  ; е)
; е)  .
.
2. Даны точки  и
и  . Написать уравнение окружности, диаметром которой служит отрезок АВ.
. Написать уравнение окружности, диаметром которой служит отрезок АВ.
3. Окружность касается оси Ох в начале координат и проходит через точку  . Написать уравнение окружности и найти точки пересечения ее с биссектрисами координатных углов.
. Написать уравнение окружности и найти точки пересечения ее с биссектрисами координатных углов.
4. Составить уравнение окружности, проходящей через точки  и
и  .
.
5. Установить, что каждое из следующих уравнений определяет эллипс, найти его центр С и полуоси:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
6. Составить каноническое уравнение эллипса, проходящего через точки 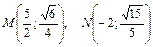 .
.
7. Установить, что каждое из следующих уравнений определяет гиперболу, найти ее центр С и полуоси:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
8. На гиперболе  взята точка М с ординатой, равной 1. Найти расстояние ее от фокуса.
взята точка М с ординатой, равной 1. Найти расстояние ее от фокуса.
9. Написать уравнение параболы:
а) проходящей через точки (0;0) и (1;-3) и симметричной относительно оси Ох;
б) проходящей через точки (0;0) и (2;-4) и симметричной относительно оси Оу.
10. Установить, что каждое из следующих уравнений определяет параболу, найти координаты ее вершины и величину параметра р:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.