Расчет предварительно напряженного элемента по бетонной полосе между наклонными сечениями произвожу из условия:
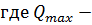наибольшее значение поперечной силы от внешней нагрузки (опорная реакция),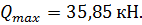 
коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, принимаем равным 1.
коэффициент, учитывающий способность бетона к перераспределению усилий;
где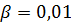 
для тяжелых бетонов
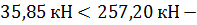условие выполняется
Расчет предварительно напряженного изгибаемого элемента по наклонному сечению произвожу из условия:
поперечная сила, воспринимаемая бетоном в наклонном сечении;
поперечная сила, воспринимаемая хомутами в наклонном сечении;
В качестве поперечной арматуры принимаю четыре каркаса на приопорных участках длиной 
с арматурой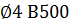 
и шагом поперечных стержней 80мм (
), тогда:
где 
поперечная сила, воспринимаемая хомутами на единицу длины плиты;
площадь сечения хомутов, расположенных в одной нормальной к оси элемента плоскости, 
где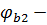 
коэффициент, принимаемый равным 1,5.
где 
длина проекции опасной наклонной трещины
Для проекции наклонной трещины должны выполняться условия:
Условия по ограничению длины проекции наклонной трещины соблюдены, для дальнейшего расчета принимаем 
.
длина проекции наиболее опасного наклонного сечения
Для проекции наиболее опасного наклонного сечения должны выполняться условия:
Верхнее ограничение не соблюдено, поэтому для дальнейшего расчета принимаю 
Тогда поперечное усилие, воспринимаемое бетоном:
Поперечная арматура требуется по расчету.
Суммарное усилие, воспринимаемое сечением:
Прочность балки по наклонной трещине обеспечена.
Расчет по предельным состояниям второй группы
|
|
Определение приведенного сечения
Для расчетов по предельным состояниям второй группы фактическое сечение плиты (рисунок 3.4) привожу к двутавровому (рисунок 3.6), заменяя круглые отверстия на квадратные со стороной 
. Тогда расчетные толщины полок двутаврового сечения:
Ширина нижней полки равна ширине плиты 
, верхней –
. Расчетная ширина ребра:
b
f
'
=1460
b
f
=1490
b=536,6
'
y
1
y
2
y
3
Рисунок 2.6− Приведенное двутавровое сечение плиты
Площадь приведенного сечения будет равна:
Статический момент приведенного сечения относительно нижней грани:
Расстояние от центра тяжести приведенного сечения до нижней грани:
Момент инерции приведенного сечения относительно его центра тяжести будет равен:
где 
Момент сопротивления сечения по нижней зоне:
Момент сопротивления сечения по верхней зоне:
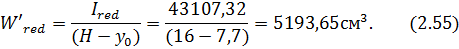
Находим упругопластический момент сопротивления относительно нижней грани:
Значение коэффициента 
, учитывающего пластические свойства бетона, для двутаврового приведенного симметричного сечения многопустотной плиты равным 1,25 (т.к. 
).
Упругопластический момент сопротивления относительно верхней грани:
