Движения в пространстве.
Симметрия относительно плоскости (зеркальная симметрия):
Определение. Преобразование пространства, при котором сохраняются расстояния между любыми двумя точками, называется движением пространства.
Свойства: при движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми.
Две фигуры называются равными, если они совмещаются движением.
В качестве примера движения пространства на данном этапе изучения стереометрии можно привести преобразование центральной симметрии, доказав координатным способом, что при этой симметрии сохраняются расстояния между точками.
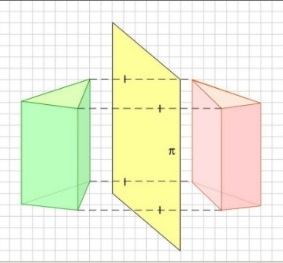
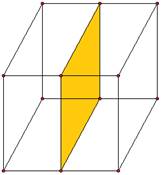
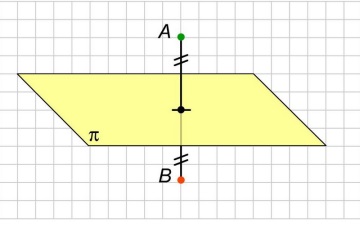
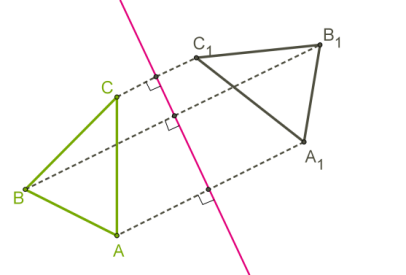
Введем понятие симметрии относительно плоскости:
Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости, называется симметрией пространства относительно плоскости. Плоскость называется плоскостью симметрии.
Примеры симметрии относительно плоскости:
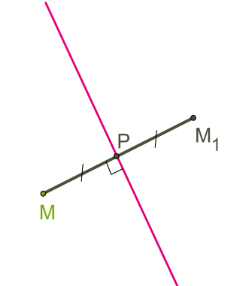
Параллельный перенос:
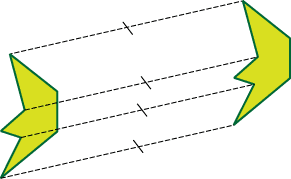
Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка отображается на такую точку, что выполняется векторное равенство. Это перенос (движение) всех точек пространства в одном и том же направлении, на одно и то же расстояние
Если плоскость (прямая) не параллельна вектору переноса, то при переносе на этот вектор она отображается на параллельную ей плоскость (прямую).
Примеры параллельного переноса:
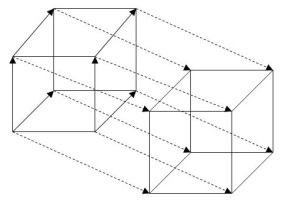

Осевая симметрия:
Определение. Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Подобие:
Определение. Преобразования фигурыв фигуру называется преобразования подобия, если при этом преобразовании расстояние между точками изменяется в одно и тоже число раз. То есть преобразование, которое сохраняет форму фигуры, но изменяет их размеры.

Гомотетия:
Определение. Гомотетия — это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).
Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент.
На рисунке из фигуры можно получить фигуру гомотетией
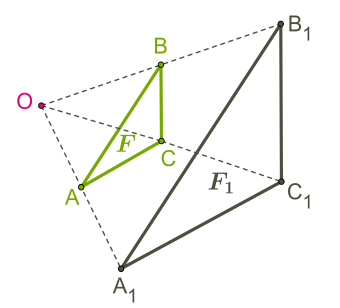
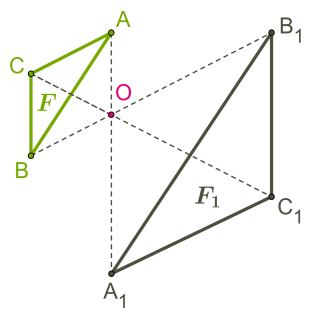
Если фигуры находятся на противоположных направлениях от центра гомотетии, то коэффициент отрицательный.
На следующем рисунке из фигуры можно получить фигуру гомотетией. В отличие от гомотетии, геометрические преобразования — центральная симметрия, осевая симметрия, поворот, параллельный перенос являются движением, т.к. в них фигура отображается в фигуру, равную данной.
Гомотетичные фигуры подобны, но подобные фигуры не всегда гомотетичны (в гомотетии важно расположение фигур).
В орнаментах (на рисунке фракталы) можно видеть бесконечное множество подобных фигур, но обычно они не гомотетичны, т.к. у них невозможно определить центр гомотетии.
Ссылка на сообщество МАТЕМАТИКА в контакте https://vk.com/club194177059