Типы графов
Орграф 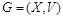 , в котором для любой пары
, в котором для любой пары  существует неориентированное ребро
существует неориентированное ребро  в
в  , называется полным. Неориентированный граф
, называется полным. Неориентированный граф 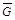 в этом случае тоже будет полным (см. рис.1.11,а, б)
в этом случае тоже будет полным (см. рис.1.11,а, б)
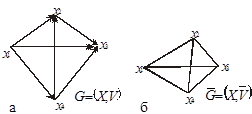
|
| Рис.1.11. Полные графы |
Граф называется симметрическим (симметричным), если
 ,
,
а граф, для которого
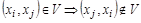 ,
,
называется антисимметрическим (антисимметричным). В таком графе нет петель. Примеры симметрического и антисимметрического графов приведены на рис.1.12, а, б

|
| Рис.1.12. Симметричный – а, и антисимметричный – б графы |
Неориентированный граф  называется двудольным, если его множество вершин может быть разбито на два подмножества
называется двудольным, если его множество вершин может быть разбито на два подмножества  и
и  таких, что
таких, что  ,
, 
 и каждое ребро имеет один конец в
и каждое ребро имеет один конец в  , а второй – в
, а второй – в  , т.е.
, т.е.  или
или 
 .
.
Орграф  называется двудольным, если соответствующий неориентированный граф
называется двудольным, если соответствующий неориентированный граф 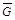 – двудольный. На рис.1.13 представлен двудольный орграф.
– двудольный. На рис.1.13 представлен двудольный орграф.

|
| Рис.1.13. Двудольный граф |
Матричное представление графов
Пусть задан орграф  , причем
, причем 
Тогда матрицей смежности орграфа  называется квадратная матрица
называется квадратная матрица  порядка
порядка 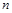 , у которой:
, у которой:
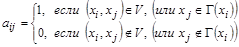
Матрицей инцидентности (инцдиенций) орграфа  называется
называется  – матрица
– матрица  , у которой:
, у которой:

Подобным же образом вводятся перечисленные матрицы для неориентированных графов, только в неориентированном графе  , если
, если  инцидентно
инцидентно  , и
, и  в противном случае. Для орграфа на рис.1.14 матрицы смежности и инциденций представлены в табл.1.1 и 1.2 соответственно.
в противном случае. Для орграфа на рис.1.14 матрицы смежности и инциденций представлены в табл.1.1 и 1.2 соответственно.

| Таблица 1.1. Матрица смежностей | Таблица 1.2. Матрица инциденций |

| 
| |
Рис.1.14. Орграф 
|
Очевидно, что матрица  является симметричной матрицей. По матрице смежности орграфа (графа) всегда можно определить дуги (ребра) графа и восстановить граф полностью (без нумерации дуг). То же можно и сказать о матрице инциденций, стоит только заметить, что невозможно установить вершину, к которой прикреплена петля (см. на рис.1.14 и табл.1.2.).
является симметричной матрицей. По матрице смежности орграфа (графа) всегда можно определить дуги (ребра) графа и восстановить граф полностью (без нумерации дуг). То же можно и сказать о матрице инциденций, стоит только заметить, что невозможно установить вершину, к которой прикреплена петля (см. на рис.1.14 и табл.1.2.).
Можно привести очевидные свойства матриц смежности и инциденций:
1. Сумма элементов матрицы смежности  равна числу дуг в графе, т.е.:
равна числу дуг в графе, т.е.:
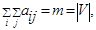 для
для 
 .
.
2. Суммы элементов матрицы  по строкам и столбцам равны полустепени исхода и захода каждой вершины соответственно, т.е.:
по строкам и столбцам равны полустепени исхода и захода каждой вершины соответственно, т.е.:
 и
и  .
.
3. В матрице инциденций  для каждого столбца сумма элементов равна нулю, т.е.:
для каждого столбца сумма элементов равна нулю, т.е.:
 .
.
4. Любая строка матрицы  является линейной комбинацией остальных строк.
является линейной комбинацией остальных строк.
5. Ранг матрицы  не превосходит
не превосходит  , где
, где  .
.
6. Для любого цикла в  сумма столбцов матрицы
сумма столбцов матрицы  , соответствующих дугам, входящим в этот цикл, равна нулевому столбцу.
, соответствующих дугам, входящим в этот цикл, равна нулевому столбцу.
Обозначим через 
 -ю степень матрицы смежности
-ю степень матрицы смежности  ,
,  ;
;  2,3,4,…
2,3,4,…
Объединение, пересечение графов, подграфы
В силу задания графа  через множества
через множества  и
и  объединением графов
объединением графов  и
и  называется граф
называется граф
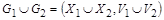 .
.
Пересечением графов  ,
,  , где
, где  , называется граф
, называется граф
 .
.
Подграфом графа  называется граф
называется граф  такой, что
такой, что  и
и  причем подграф
причем подграф  называется остовным, если
называется остовным, если  .
.
 Порожденным подграфом
Порожденным подграфом  называется такой подграф графа
называется такой подграф графа  , что
, что  и.
и.
Достижимость, связность, компоненты связности, конденсация графа
Говорят, что для орграфа  вершина
вершина  достижима из
достижима из  , если либо
, если либо  , либо существует путь из
, либо существует путь из  в
в  (для неориентированного графа маршрут, соединяющий
(для неориентированного графа маршрут, соединяющий  и
и  ).
).
Тогда для каждой вершины орграфа  можно ввести множество достижимых из нее вершин
можно ввести множество достижимых из нее вершин 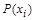 с помощью порождающей процедуры:
с помощью порождающей процедуры:
 , (1.1)
, (1.1)
где, очевидно,  , и определить матрицу достижимости
, и определить матрицу достижимости  :
:
 (1.2)
(1.2)
Через множества контрдостижимых вершин (из которых достижима  )
)  :
:
 ,
,
определяем матрицу контрдостижимости  :
:
 (1.3)
(1.3)
Из определения  и
и  следует, что
следует, что  .
.
Действительно, если в матрице достижимости  элемент
элемент 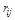 равен 1, то это значит, что существует путь из вершины
равен 1, то это значит, что существует путь из вершины  в
в  . Но одновременно это же означает, что вершина
. Но одновременно это же означает, что вершина  достижима из
достижима из  , а это определяет в матрице
, а это определяет в матрице  равенство для элемента
равенство для элемента  =1.
=1.
Если же в матрице достижимости 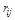 =0, т.е. из вершины
=0, т.е. из вершины  невозможно достичь
невозможно достичь  , то одновременно можно утверждать, что вершина
, то одновременно можно утверждать, что вершина  недостижима из
недостижима из  , а это значит, что
, а это значит, что  =0 для матрицы контрдостижимости.
=0 для матрицы контрдостижимости.
Таким образом, мы доказали, что  , а это и доказывает наше утверждение.
, а это и доказывает наше утверждение. 
Для примера рассмотрим орграф на рис.1.17,а и составим для него часть множеств  (рис.1.17,б) и матрицу достижимостей
(рис.1.17,б) и матрицу достижимостей  (рис.1.17,в).
(рис.1.17,в).

|
| Рис.1.17. Орграф (а) и соответствующие ему множества достижимости, контрдостижимости (б), матрица достижимости (в) |
Очевидно, что множество  определяет множество вершин, достижимых из
определяет множество вершин, достижимых из  , для которых
, для которых  является достижимой. Таким образом, любая вершина
является достижимой. Таким образом, любая вершина  лежит хотя бы на одном пути из
лежит хотя бы на одном пути из  в
в  . Такие вершины называются существенными относительно концевых вершин
. Такие вершины называются существенными относительно концевых вершин  и
и  , а любая вершина
, а любая вершина  называется избыточной относительно пути из
называется избыточной относительно пути из  в
в  .
.
Граф (орграф) называется связным (сильно связным), если для любых  ,
,  существует маршрут (путь) из
существует маршрут (путь) из  в
в  .
.
Односторонне связным называется орграф, если для любых  ,
, 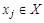 существует путь из
существует путь из  в
в  или из
или из  в
в  .
.
Орграф называется слабо связным, если связным является ассоциированный с ним неориентированный граф. Если граф (орграф) не является связным (слабо связным), то он называется несвязным.
Если в исходном графе можно выделить подграф G=(x,v), такой, что для вершин выполняется условие:  достижима из
достижима из  и
и  (т.е. все вершины взаимодостижимы), то такой подграф называется сильной (связной) компонентой (СК).
(т.е. все вершины взаимодостижимы), то такой подграф называется сильной (связной) компонентой (СК).
Очевидно, что элементы СК определяются множеством  . Пусть
. Пусть  . Найдем очередную СК
. Найдем очередную СК  , так чтобы
, так чтобы  . Получим множество вершин новой СК
. Получим множество вершин новой СК  . Продолжим процесс выделения СК до тех пор, пока они иссякнут. Тогда сформируем граф
. Продолжим процесс выделения СК до тех пор, пока они иссякнут. Тогда сформируем граф  такой, что
такой, что  есть выделенные СК, а дуга
есть выделенные СК, а дуга  существует в
существует в  тогда и только тогда, когда в
тогда и только тогда, когда в  существует дуга
существует дуга  такая, что
такая, что  , а
, а  , причем такая, что
, причем такая, что  . Полученный таким образом граф
. Полученный таким образом граф  называется конденсацией. На рис.1.18,б представлены все СК графа
называется конденсацией. На рис.1.18,б представлены все СК графа  из рис.1.18,а, а конденсация
из рис.1.18,а, а конденсация  представлена на рис.1.18,в
представлена на рис.1.18,в

|
| Рис.1.18. Построение конденсации графа |
 Если положить, что для графа
Если положить, что для графа  построена матрица достижимости
построена матрица достижимости  , то можно предложить эффективный метод выделения всех СК и построения конденсации.
, то можно предложить эффективный метод выделения всех СК и построения конденсации.
Для этого введем матрицу, где символ  обозначает прямое произведение матриц, при котором элементы матрицы
обозначает прямое произведение матриц, при котором элементы матрицы  (
( ) определяются соотношением
) определяются соотношением  . Тогда для элементов матрицы
. Тогда для элементов матрицы  справедливо:
справедливо:  .
.
Поскольку все вершины  достижимы и контрдостижимы для себя же (
достижимы и контрдостижимы для себя же ( ), то
), то  . Если же
. Если же 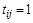 для
для  , это значит, что
, это значит, что  и
и  , а следовательно вершина
, а следовательно вершина  достижима из
достижима из  , а вершина
, а вершина  достижима из
достижима из  , а следовательно, они взаимодостижимы и входят в одну СК.
, а следовательно, они взаимодостижимы и входят в одну СК.
Так, для графа на рис.1.18 матрицы  и
и  имеют вид:
имеют вид:

 .
.
Тогда алгоритм выделения СК и построения конденсации может иметь следующий вид (далее  – множество вершин конденсации,
– множество вершин конденсации,  – множество задействованных уже в СК вершин,
– множество задействованных уже в СК вершин,  - текущая СК,
- текущая СК,  - текущее число СК в графе):
- текущее число СК в графе):
Шаг 1. Установка начальных значений: 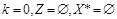 .
.
Шаг 2. Контроль для выхода. Если  идти в конец, (шаг 4), иначе к шагу 3.
идти в конец, (шаг 4), иначе к шагу 3.
Шаг 3. Выделение СК. Полагаем  . Для
. Для  ,
,  , формируем
, формируем  ,
,  ,
,  . Переходим к шагу 2.
. Переходим к шагу 2.
Шаг 4. Окончание.
 ,
,  .
.
Для графа на рис. 1.18,а в результате работы алгоритма получим таблицу пошаговых преобразований:

| 
| 
| 
|  
|

| Ø | Ø | Ø | |

| 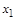
| 
| 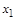
| |

| 
| 
| 
| |
| Ø | 
| 
| 
|
Для матрицы смежности  размером 3х3 получим отличные от нуля элементы:
размером 3х3 получим отличные от нуля элементы:
 , т.к. существует дуга, например
, т.к. существует дуга, например  , такая, что
, такая, что  и
и  ;
;
 ,т.к. существует дуга, например
,т.к. существует дуга, например  , такая, что
, такая, что  и
и 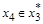 ;
;
 ,т.к. существует дуга, например
,т.к. существует дуга, например  , такая, что
, такая, что  и
и 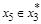 .
.
Остальные элементы равны нулю. Тогда
 ,
,
что и отражено на рисунке 1.18,б и 1.18,в.
Теперь для конденсации графа, поскольку это уже ациклический граф, можно построить иерархическую структуру, в которой вершины расположены по уровням  так, что дуги исходного графа (или конденсации)
так, что дуги исходного графа (или конденсации)  направлены так, что для
направлены так, что для 
 ,
,  Þ
Þ  .
.
Алгоритм построения иерархической структуры графа  может иметь вид:
может иметь вид:
Начальное состояние:  ,
,  ,
,  ,
, 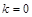 .
.
Шаг 1. Контроль непустоты графа. Если  Æ идти в конец (шаг 4), иначе к шагу 2.
Æ идти в конец (шаг 4), иначе к шагу 2.
Шаг 2. Построение уровня. Для  ,
,  .
.
Шаг 3. Формирование рабочих множеств. Удаление выделенных вершин и дуг, исходящих из них:
 ,
,  ,
, 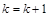 и идти к шагу 1.
и идти к шагу 1.
Шаг 4. Вывод глубины иерархической структуры  , и состава уровней
, и состава уровней  ,
,  .
.
В литературе определяют также компоненту сильной связности для орграфа как его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа орграфа  .
.
Так, у орграфа на рис.1.19,а три компоненты сильной связности, показанные в рис.1.19, б, в, г.

|
| Рис.1.19. Компоненты сильной связности (б), (в), (г) орграфа (а) |
Исходя из определения компонент сильной связности, можно утверждать, что:
Базы и антибазы
База  графа
графа  определена как множество вершин
определена как множество вершин  таких, что:
таких, что:
 и
и  , (1.4)
, (1.4)
где 
Второе условие  в (1.4) эквивалентно утверждению, что
в (1.4) эквивалентно утверждению, что  для любых
для любых  , что определит базу как множество вершин графа
, что определит базу как множество вершин графа  , удовлетворяющее условиям:
, удовлетворяющее условиям:
а)  ,
,
б)  .
.
Антибаза  графа
графа 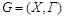 есть множество вершин таких, что:
есть множество вершин таких, что:
 и
и  . (1.5)
. (1.5)
 обладает свойством минимальности в том смысле, что удаление любой вершины из
обладает свойством минимальности в том смысле, что удаление любой вершины из  лишает ее основного свойства.
лишает ее основного свойства.

|
| Рис.1.20. Базы и антибазы |
Для графа на рис.1.20,а приведены списки баз и антибаз (рис.1.20, б, в), определяющих минимальные множества: множества  – из которых достижимы остальные вершины графа, антибазы
– из которых достижимы остальные вершины графа, антибазы  – вершины которых достижимы из какой-нибудь вершины вне антибазы
– вершины которых достижимы из какой-нибудь вершины вне антибазы  .
.
Если граф  представляет собой структуру руководства (влияния) в некоторой организации, то базу
представляет собой структуру руководства (влияния) в некоторой организации, то базу  можно интерпретировать как «коалицию», включающую наименьшее число лиц, обладающих властью над каждым членом организации.
можно интерпретировать как «коалицию», включающую наименьшее число лиц, обладающих властью над каждым членом организации.
Если теперь для той же организации построен граф каналов связи (с направлением передачи информации)  , то очевидно, что
, то очевидно, что 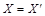 , но
, но  . Тогда можно утверждать, что эффективная для управления этой организации «коалиция» будет являться множеством
. Тогда можно утверждать, что эффективная для управления этой организации «коалиция» будет являться множеством  , где
, где  одна из баз графа
одна из баз графа  и одна из антибаз графа
и одна из антибаз графа  , выбранные так, чтобы
, выбранные так, чтобы  было минимальным.
было минимальным.
Чтобы избежать влияния на  извне (если
извне (если  и
и  ), можно определить сильную базу
), можно определить сильную базу  , такую что
, такую что 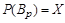 ,
,  и
и  , для
, для  (т.е. включить в B все вершины СК) и использовать это понятие для формирования структур управления.
(т.е. включить в B все вершины СК) и использовать это понятие для формирования структур управления.
Для построения базы ацикличного орграфа достаточно выделить множество вершин с полустепенью захода, равной нулю, т.е.:
 ,
,
а для антибазы
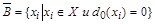 .
.
Таким образом, для ациклических графов 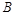 и
и  единственны. Для графа, содержащего СК
единственны. Для графа, содержащего СК  , необходимо построить конденсацию
, необходимо построить конденсацию  и выделить базу
и выделить базу  :
:
 .
.
Тогда базой  в
в  будет являться любое множество вершин
будет являться любое множество вершин
 (1.6)
(1.6)
где  – пронумерованные СК, составляющие базу
– пронумерованные СК, составляющие базу  в
в 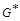 .
.
Соотношение (1.6) определяет множество баз в  , состоящих из вершин, взятых по одной из каждой
, состоящих из вершин, взятых по одной из каждой  .
.