Метод математической статистики получил широкое распространение для обработки результатов различных исследований. В технологии машиностроения он применяется для анализа точности технологических процессов, работы металлорежущего оборудования и статистического контроля в процессе производства.
Задачами статистического анализа точности технологического процесса являются:
1.Определение суммарной точности механической обработки деталей.
2.Определение точности настройки станка.
3.Определение стабильности разработанного технологического процесса с выявлением и анализом причин, вызывающих его разрушение.
Металлорежущим станкам присущи погрешности взаимного расположения узлов и деталей. Поэтому при получении заданных размеров партии деталей неизбежны погрешности. Одни причины могут увеличивать размер детали, другие- уменьшать его. Алгебраическая сумма погрешностей, действующих одновременно, образует суммарную или результирующую погрешность обработки. Она является мерой точности выбранного метода обработки и режимов резания.
Для определения ожидаемой суммарной погрешности обработки пользуются следующими тремя методами:
1)с помощью таблиц экономической точности обработки;
2)статистическим методом анализа точности обработки;
3)расчетно-аналитическим методом.
Появление действительно размера у очередной обрабатываемой детали является случайным событием, а значение размера будет случайной величиной. Все случайные размеры обладают закономерностями, которые можно изобразить в виде кривых распределения в зависимости от вида погрешности.
По закономерностям появления погрешности делятся на систематические, случайные и грубые.
Систематические постоянные погрешности не изменяются по величине при обработке одной или нескольких партий заготовок и возникают под влияние действия постоянного фактора.
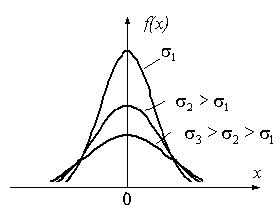
Рис1.1 изменение формы кривой нормального распределения в зависимости от среднего квадратичного отклонения размера.
Ход выполнение лабораторной работы
| № п/п | di,мм | di-dср,мм | (di-dср)²,мм |
| 24,54 | -0,20 | 0,0382 | |
| 24,72 | -0,02 | 0,0002 | |
| 24,77 | 0,03 | 0,0012 | |
| 24,61 | -0,13 | 0,0157 | |
| 24,78 | 0,04 | 0,0020 | |
| 24,74 | 0,00 | 0,0000 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,71 | -0,03 | 0,0006 | |
| 24,78 | 0,04 | 0,0020 | |
| 24,70 | -0,04 | 0,0013 | |
| 24,86 | 0,12 | 0,0155 | |
| 24,71 | -0,03 | 0,0006 | |
| 24,65 | -0,09 | 0,0073 | |
| 24,70 | -0,04 | 0,0013 | |
| 24,74 | 0,00 | 0,0000 | |
| 24,56 | -0,18 | 0,0308 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,71 | -0,03 | 0,0006 | |
| 24,70 | -0,04 | 0,0013 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,66 | -0,08 | 0,0057 | |
| 24,82 | 0,08 | 0,0072 | |
| 24,78 | 0,04 | 0,0020 | |
| 24,79 | 0,05 | 0,0030 | |
| 24,78 | 0,04 | 0,0020 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,65 | -0,09 | 0,0073 | |
| 25,32 | 0,58 | 0,3418 | |
| 24,74 | 0,00 | 0,0000 | |
| 24,75 | 0,01 | 0,0002 | |
| 24,72 | -0,02 | 0,0002 | |
| 24,72 | -0,02 | 0,0002 | |
| 24,73 | -0,01 | 0,0000 | |
| 24,75 | 0,01 | 0,0002 | |
| 24,82 | 0,08 | 0,0072 | |
| 24,62 | -0,12 | 0,0133 | |
| 24,58 | -0,16 | 0,0241 | |
| 24,63 | -0,11 | 0,0111 | |
| 24,63 | -0,11 | 0,0111 | |
| 24,58 | -0,16 | 0,0241 | |
| 24,76 | 0,02 | 0,0006 | |
| 24,74 | 0,00 | 0,0000 | |
| 24,81 | 0,07 | 0,0056 | |
| 24,98 | 0,24 | 0,0598 | |
| 24,68 | -0,06 | 0,0031 | |
| 24,73 | -0,01 | 0,00003 | |
| 24,72 | -0,02 | 0,0002 | |
| 24,74 | 0,00 | 0,00002 | |
| dср. | 24,74 |
Данные для построения графика рассеяния действительных размеров.
| № п/п | граница интервала, мм | частота,мм |
| 24,54 | ||
| 24,67 | 11,00 | |
| 24,8 | 33,00 | |
| 24,93 | 4,00 | |
| 25,06 | 1,00 | |
| 25,19 | 0,00 | |
| 25,32 | 1,00 |
Данные для построения теоретической кривой нормального распределения
| x | y | ∆d | 0,13 |
| 24,93 | 22,76079 | σ | 0,11 |
| 25,04 | 13,65648 | ||
| 24,82 | 13,65648 | ||
| 25,27269 | |||
| 24,58731 |
Теоретическая кривая нормального распределения и графика рассеяния действительных размеров.
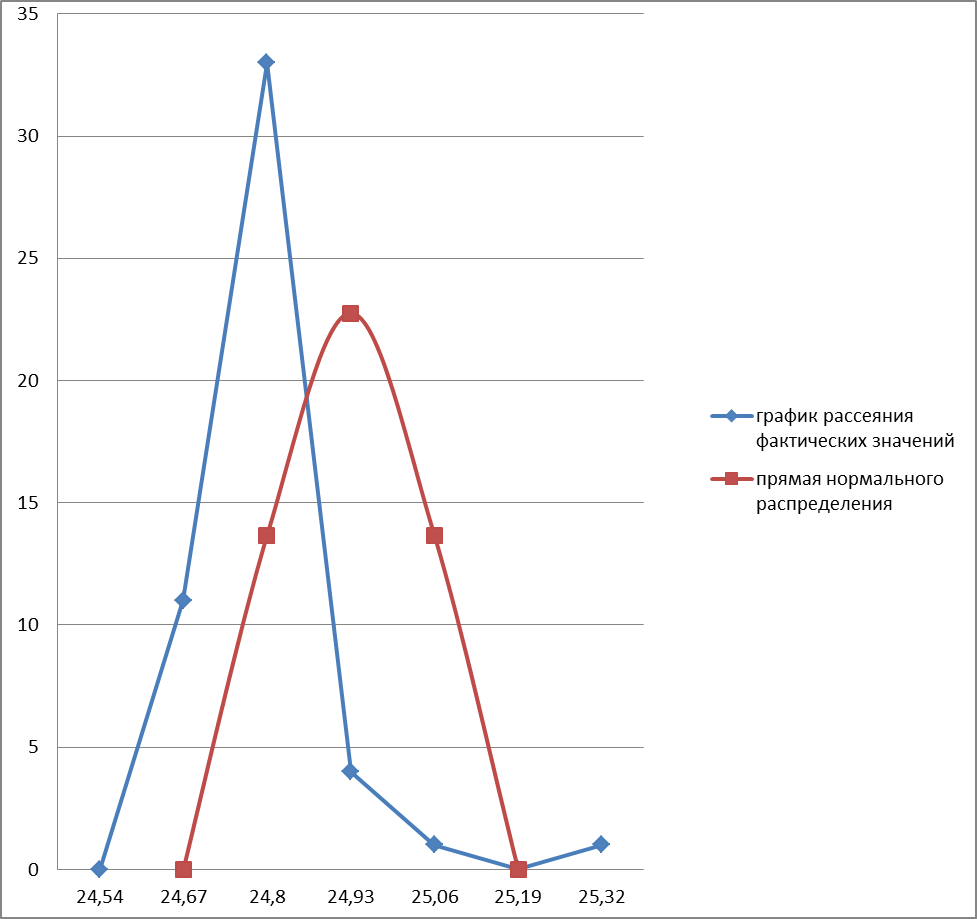
Оценка вероятности получения годных деталей для конкретного технологического процесса
Вероятность получения годных деталей:
P=(Ф(z1)+Ф(z2))
Общий процент брака:
P1=100-P
Так как брак может быть исправим, тогда вероятность получения деталей с размерами меньшими, чем заданные, будет составлять:
P`=[0,5-Ф(z1)]100,%,
а вероятность получения деталей с размерами большими, чем заданные, будет составлять
P``=[0,5-Ф(z2)]100,%
Зная среднеквадратичное отклонение и максимальное допустимое отклонение, определяем отношение:
z=δ/σ
Вероятность соблюдения заданного допуска обработки равна:
P=n/N=Ф(z)
Вывод: в ходе выполнения данной лабораторной работы мы ознакомились с методикой использования методов математической статистики в технологии машиностроения, построили теоретическую кривую нормального распределения и график рассеяния действительных размеров, анализирую данный график мы пришли к выводу, что при изготовление данных деталей не учли их тепловое увеличение в результате обработки.