Дата 17.04.2020
Практическая работа № 7
Тема: Расчет разъемных и неразъемных соединений на прочность.
Цель: Ознакомить с расчетами разъемных и неразьемных соединений.
Задание:
1. Внимательно ознакомиться с методиками расчетов разъемных и неразьемных соединений.
2.Из предложенных примеров выбрать и записать:
А) разъемного соединения
Б) неразьемного соединения
3.Обосновать причину выбора примеров.
4. Вывод
Теоретические сведения
Расчет крепежных резьбовых соединений
Основным критерием работоспособности крепежных резьбовых соединений является прочность.
Стандартные крепежные детали сконструированы равнопрочными по следующим параметрам: по напряжениям среза и смятия в резьбе, напряжениям растяжения в нарезанной части стержня и в месте перехода стержня в головку. Поэтому для стандартных крепежных деталей в качестве главного критерия работоспособности принята прочность стержня на растяжение, и по ней ведут расчет болтов, винтов и шпилек. Расчет резьбы на прочность выполняют в качестве проверочного лишь для нестандартных деталей.
Расчет резьбы. Как показали исследования, проведенные Н.Е. Жуковским, силы взаимодействия между витками винта и гайки распределены в значительной степени неравномерно, однако действительный характер распределения нагрузки по виткам зависит от многих факторов, трудно поддающихся учету (неточности изготовления, степени износа резьбы, материала и конструкции гайки и болта и т.д.). Поэтому при расчете резьбы условно считают, что все витки нагружены одинаково, а неточность в расчете компенсируют значением допускаемого напряжения.
Условие прочности резьбы на срез имеет вид
|
|
τcp= Q / А cp) ≤[τcp],
где Q– осевая сила; A ср– площадь среза витков нарезки; для винта A ср= π d 1 kH г, для гайки
А ср = π DkH г.
Здесь Н г – высота гайки;
k– коэффициент, учитывающий ширину основания витков резьбы: для метрической резьбы для винта k ≈ 0,75, для гайки k ≈ 0,88;
для трапецеидальной и упорной резьб k ≈ 0,65; для прямоугольной резьбы k = 0,5.
Если винт и гайка из одного материала, то на срез проверяют только винт, так как d l < D.
Условие прочности резьбы на смятие имеет вид
σcм= Q / А cм≤[σcм],
где А см – условная площадь смятия (проекция площади контакта резьбы винта и гайки на плоскость, перпендикулярную оси):
А см = π d 2 hz, где nd 2 – длина одного витка по среднему диаметру;
h– рабочая высота профиля резьбы; z= Н г/ р – число витков резьбы в гайке высотой Н г; р – шаг резьбы (по стандарту рабочая высота профиля резьбы обозначена Н 1).
Расчет незатянутых болтов.
Характерный пример незатянутого резьбового соединения – крепление крюка грузоподъемного механизма (рис.1).
Под действием силы тяжести груза Q стержень крюка работает на растяжение, а опасным будет сечение, ослабленное нарезкой.
Статическая прочность стержня с резьбой (которая испытывает объемное напряженное состояние) приблизительно на 10% ниже, чем гладкого стержня без резьбы. Поэтому расчет стержня с резьбой условно ведут по расчетному диаметру dp= d– 0,9 р, где р – шаг резьбы с номинальным диаметром d (приближенно можно считать dp ≈ d 1). Условие прочности нарезанной части стержня на растяжение имеет вид
σp= Q / А p≤[σp],
где расчетная площадь Ар = 
.
|
|
Расчетный диаметр резьбы d р 
.По найденному значению расчетного диаметра подбирается стандартная крепежная резьба.
Расчет затянутых болтов
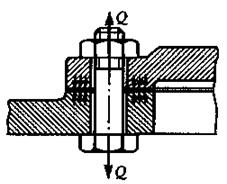
Пример затянутого болтового соединения – крепление крышки люка с прокладкой, где для обеспечения герметичности необходимо создать силу затяжки Q. При этом стержень болта растягивается силой Q и скручивается моментом М р в резьбе.
Напряжение растяжения σp= Q /(π 
/4), максимальное напряжение кручения τк = М р/ W p, где: Wp= 0,2 
– момент сопротивления кручению сечения болта; М р = 0,5 Qd2 tg(ψ + φ').
Подставив в эти формулы средние значения угла подъема ψ резьбы, приведенного угла трения φ' для метрической крепежной резьбы, и применяя энергетическую теорию прочности, получим
σэкв = 
.
Отсюда, согласно условию прочности σэкв ≤ [σр], запишем
σэкв = 1,3 Q /(π /4) = Q расч/(π /4) ≤[σр],
где Q расч= 1,3 Q, а [σр] – допускаемое напряжение при растяжении.
Таким образом, болт, работающий на растяжение и кручение, можно условно рассчитывать только на растяжение по осевой силе, увеличенной в 1,3 раза. Тогда
d р≥ 
.
Здесь уместно отметить, что надежность затянутого болтового соединения в значительной степени зависит от качества монтажа, т.е. от контроля затяжки при заводской сборке, эксплуатации и ремонте. Затяжку контролируют либо путем измерения деформации болтов или специальных упругих шайб, либо с помощью динамометрических ключей.
Расчет затянутого болтового соединения, нагруженного внешней осевой силой.
Примером такого соединения может служить крепление z болтами крышки работающего под внутренним давлением резервуара Для такого соединения необходимо обеспечить отсутствие зазора между крышкой и резервуаром при приложении нагрузки Rz, иначе говоря, обеспечить не раскрытие стыка. Введем следующие обозначения: Q– сила первоначальной затяжки болтового соединения; R – внешняя сила, приходящаяся на один болт; F– суммарная нагрузка на один болт (после приложения внешней силы R).
|
|
Очевидно, что при осуществлении первоначальной затяжки болтового соединения силой Q болт будет растянут, а соединяемые детали сжаты. После приложения внешней осевой силы R болт получит дополнительное удлинение, в результате чего затяжка соединения несколько уменьшится.
Поэтому суммарная нагрузка на болт F < Q+ R, задача ее определения методами статики не решается.
Для удобства расчетов условились считать, что часть внешней нагрузки R воспринимается болтом, остальная часть – соединяемыми деталями, а сила затяжки остается первоначальной, тогда F = Q+ к R, где к – коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом.
Так как до раскрытия стыка деформации болта и соединяемых деталей под действием силы R равны, то можно записать:
к R λ6=(1 – к) R λд;
λб, λд – соответственно податливость (т.е. деформация под действием силы в 1 Н) болта и соединяемых деталей. Из последнего равенства получим
к = λд/(λб + λд).
Отсюда видно, что с увеличением податливости соединяемых деталей при постоянной податливости болта коэффициент внешней нагрузки будет увеличиваться.
Поэтому при соединении металлических деталей без прокладок принимают к = 0,2...0,3, а с упругими прокладками – к = 0,4...0,5.
Очевидно, что раскрытие стыка произойдет, когда часть внешней силы, воспринятой соединяемыми деталями, окажется равной первоначальной силе затяжки, т.е. при (1 – к) R = Q. Не раскрытие стыка будет гарантировано, если
Q = K (1 – к) R,
где К – коэффициент затяжки; при постоянной нагрузке К = 1,25...2, при переменной нагрузке К = 1,5... 4.
Ранее мы установили, что расчет затянутых болтов ведется по увеличенной в 1,3 раза силе затяжки Q. Поэтому в рассматриваемом случае расчетная сила
Q расч= 1,3 Q + к R,
а расчетный диаметр болта
d р≥ .
Расчет болтовых соединений, нагруженных поперечной силой.
Возможны два принципиально отличных друг от друга варианта таких соединений.
В первом варианте болт ставится с зазорам и работает на растяжение.
Затяжка болтового соединения силой Q создает силу трения, полностью уравновешивающую внешнюю силу F, приходящуюся на один болт, т.е. F = i f Q, где i– число плоскостей трения; f – коэффициент сцепления.
Для гарантии минимальную силу затяжки, вычисленную из последней формулы, увеличивают, умножая ее на коэффициент запаса сцепления К = 1,3...1,5, тогда: Q = KF /(i f).
Расчетная сила для болта Q pacч = 1,3 Q,
расчетный диаметр болта d р≥ .
В рассмотренном варианте соединения сила затяжки до пяти раз может превосходить внешнюю силу, и поэтому диаметры болтов получаются большими. Во избежание этого нередко такие соединения разгружают установкой шпонок, штифтов (рис. б) и т.п.
Во втором варианте болт повышенной точности ставят в развернутые отверстия соединяемых деталей без зазора, он работает на срез и смятие.
Условия прочности такого болта имеют вид
τср = 4 F /(π 
i)≤ [τср], σсм = F /(d 0δ)≤[σсм],
где i – число плоскостей среза (для схемы на рис. i= 2);
d 0δ – условная площадь смятия, причем если δ > (δ1 + δ2), то в расчет (при одинаковом материале деталей) принимается меньшая величина. Обычно из условия прочности на срез определяют диаметр стержня болта, а затем проводят проверочный расчет на смятие.
Во втором варианте конструкции болтового соединения, нагруженного поперечной силой, диаметр стержня болта получается в два – три раза меньше, чем в первом варианте (без разгрузочных деталей).
Допускаемые напряжения. Обычно болты, винты и шпильки изготовляют из пластичных материалов, поэтому допускаемые напряжения при статической нагрузке определяют в зависимости от предела текучести материала, а именно:
при расчете на растяжение [σр] = σt/[ s ];
при расчете на срез [τср] = 0,4σт;
при расчете на смятие [σсм] = 0,8σт.
Значения допускаемого коэффициента запаса прочности [ s ] зависят от характера нагрузки (статическая или динамическая), качества монтажа соединения (контролируемая или неконтролируемая затяжка), материала крепежных деталей (углеродистая или легированная сталь) и их номинальных диаметров.
Ориентировочно при статической нагрузке крепежных деталей из углеродистых сталей: для незатянутых соединений [ s ]=1,5...2 (в общем машиностроении), [ s ] = 3...4 (для грузоподъемного оборудования); для затянутых соединений [ s ] = 1,3...2 (при контролируемой затяжке), [ s ]=2,5...3 (при неконтролируемой затяжке крепежных деталей диаметром более 16 мм).
Для крепежных деталей с номинальным диаметром менее 16мм верхние пределы значений коэффициентов запаса прочности увеличивают в два и более раз ввиду возможности обрыва стержня из-за перетяжки.
Для крепежных деталей из легированных сталей (применяемых для более ответственных соединений) значения допускаемых коэффициентов запаса прочности берут примерно на 25% больше, чем для углеродистых сталей.
При переменной нагрузке значения допускаемых коэффициентов запаса прочности рекомендуются в пределах [ s ] = 2,5…4, причем за предельное напряжение принимают предел выносливости материала крепежной детали.