Соединение фаз нагрузки треугольником

 

Составим расчётную схему при соединении нагрузки треугольником (рис.4.15). При этом:

i_A, i_В, i_С – линейные токи нагрузки, А;

i_aв, i_bc, i_ca – фазные токи нагрузки, А;

, , – линейные
(фазные) напряжения нагрузки, В.

 

 

Как видно из расчётной схемы, фазное напряжение нагрузки равно линейному напряжению нагрузки, то есть

Uф = Uл.

(4.23)

По первому закону Кирхгофа найдём линейные токи через фазные:

iА = iab – ica;	(4.24)
iВ = ibc – iab;	(4.25)
iС = ica – ibc.	(4.26)

Построим векторную диаграмму линейных напряжений, фазных и линейных токов (для действующих значений) на плоскости (рис.4.16).

 

Установим связь между действующими значениями фазных (I_ф) и линейных (I_л) токов нагрузки при соединении её фаз
треугольником, для чего рассмотрим
треуголь­ник токов (рис.4.17).

Из треугольника токов находим:

Iл = 2 Iф cos 30° = 2 Iф = Iф.

(4.27)

 

Вопросы для самоконтроля

1. Что понимается под фазой нагрузки?

2. Как соединяют фазы нагрузки по схеме треугольника?

3. Составьте расчётную схему нагрузки при соединении её фаз треугольником
для мгновенных значений.

4. Запишите мгновенные значения фазных (линейных) напряжений нагрузки
при соединении её фаз треугольником, приняв начальную фазу напряжения
фазы А генератора равной нулю.

5. Постройте векторную диаграмму фазных и линейных напряжений и токов
нагрузки при соединении её фаз треугольником (для действующих значений).

6. Каково соотношение между значениями фазных и линейных напряжений
нагрузки при соединении её фаз треугольником?

7. Каково соотношение между значениями фазных и линейных токов
при соединении нагрузки треугольником?

 

Мощности трёхфазной цепи

 

Каждая фаза трёхфазной нагрузки потребляет активную, реактивную и
полную мощности. При симметричной нагрузке и схеме соединения фаз нагрузки звездой эти мощности в каждой фазе можно рассчитать следующим образом:

;

;

.

Мощности, которые потребляют три фазы нагрузки, можно рассчитать,
умножив на количество фаз нагрузки (то есть на три) мощности, которые потребляет одна фаза:

;

;

.

Определим эти мощности через линейные напряжения и токи:

;

;

.

При соединении фаз нагрузки треугольником выражения (4.28) и (4.29)
справедливы, только в этих выражениях будут свои фазные токи и напряжения.
Определим эти мощности через линейные напряжения и токи:

;

;

.

 

Таким образом, мощности, потребляемые трёхфазной нагрузкой (независимо от схемы её соединения), можно рассчитать следующим образом:

;

;

.

 

Вопросы для самоконтроля

1. Как определить активную мощность, потребляемую трёхфазной нагрузкой?

2. Как определить реактивную мощность, потребляемую трёхфазной нагрузкой?

3. Как определить полную мощность, потребляемую трёхфазной нагрузкой?

 

4.6. Расчёт неразветвлённых трёхфазных цепей
синусоидального тока

 

Рассмотрим расчётную схему трёхфазной трёхпроводной электрической цепи, которая состоит из идеального генератора, соединённого звездой, идеальной линии электропередачи, нагрузки, соединённой звездой (рис.4.18).

 

 

 

Пусть задано действующее значение электродвижущей силы Е в фазе симметричного генератора и полные сопротивления фаз нагрузки

,

а также коэффициенты мощности фаз нагрузки

cos j_а = cos j_b = cos j_с = cos j.

Требуется рассчитать действующие значения фазных и линейных сил токов генератора и нагрузки, фазных и линейных напряжений генератора и нагрузки, а также мощности, отдаваемые генератором и потребляемые нагрузкой.

Алгоритм расчёта следующий:

1. Составляем расчётную схему одной фазы цепи.

Принимаем, что потенциал точки 0 равен нулю. Можно доказать, что при
симметричном режиме работы цепи потенциал точки 0’ также равен нулю.

Поэтому можно соединить точки 0 и 0’, от чего режим работы цепи
не изменится.

Выделяем одну фазу цепи (рис.4.19).

 

 

2. Определяем действующие значения сил токов.

В данном случае фазный ток генератора равен линейному току и равен фазному току нагрузки. Например, для фазы А он равен:

.

Другие токи I_в и I_с равны току I_а.

3. Определяем действующие значения фазных напряжений.

В данном случае фазные напряжения генератора равны фазным напряжениям нагрузки. Например, для фазы а оно равно:

.

Другие напряжения U_а, U_в, U_с, U_b, U_с равны U_а.

4. Определяем действующие значения линейных напряжений.

В данном случае линейные напряжения генератора равны линейным напряжениям нагрузки. Например:

.

Другие напряжения U_ав, U_вс, U_са, U_bс, U_са равны U_аb.

5. Определяем активную мощность.

В данном случае активная мощность, отдаваемая генератором, равна активной мощности, потребляемой нагрузкой:

или

,

где U_ф и U_л – соответственно фазное и линейное напряжения, В;

I_ф и I_л – соответственно фазный и линейный токи, А.

6. Определяем реактивную мощность.

В данном случае реактивная мощность, отдаваемая генератором, равна реактивной мощности, потребляемой нагрузкой:

или

.

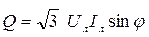7. Определяем полную мощность.

В данном случае полная мощность, отдаваемая генератором, равна полной мощности, потребляемой нагрузкой:

или

.

Пример 4.3

Трёхфазная симметричная нагрузка получает питание от трёхфазного
симметричного генератора с помощью идеальной линии электропередачи. Генератор
соединён звездой, нагрузка соединена звездой, линия электропередачи трёхпроводная. Активное сопротивление фазы нагрузки равно 12 Ом, индуктивное сопротивление фазы нагрузки равно 16 Ом. Действующее значение э.д.с. в фазе генератора равно 300 В.

Рассчитать данную трёхфазную электрическую цепь.

Решение.

1. Расчётная схема цепи приведена на рис.4.18, а для одной фазы – на рис.4.19.

2. Определяем полные сопротивления нагрузки:

.

3. Определяем действующие значения фазных и линейных сил токов
генератора и нагрузки:

.

4. Определяем действующие значения фазных напряжений
генератора и нагрузки:

.

5. Определяем действующие значения линейных напряжений
генератора и нагрузки:

.

6. Определяем угол сдвига фаз нагрузки:

.

7. Определяем активную мощность,
отдаваемую генератором и потребляемую нагрузкой:

.

8. Определяем реактивную мощность
генератора и нагрузки:

.

9. Определяем полную мощность,
отдаваемую генератором и потребляемую нагрузкой:

.

Вопросы для самоконтроля

1. Составьте расчётную схему трёхфазной цепи, состоящей из трёхфазного идеального генератора, соединённого звездой, идеальной трёхпроводной линии электропередачи,
нагрузки, соединённой звездой.

2. Приведите алгоритм расчёта указанной цепи, если задано действующее значение электродвижущей силы в фазе генератора, полные сопротивления фаз нагрузки,
а также коэффициенты мощности фаз нагрузки.