Цель работы. Практическое усвоение формул обработки неравноточных измерений одной величины, освоение методов определения наиболее достоверного значения измеренной величины, оценки точности неравноточных измерений.
Исходные данные. Вариант получают моделированием в программе MATRIX.exe.
Состав задания. Между двумя реперами выполняется измерение превышений по десяти ходам различной длины. В результате повторных неравноточных измерений получен ряд
h1, h 2,............, h 7
с длинами
L1, L2,..........., L7
По результатам измерений надо вычислить:
- наиболее достоверное значение измеренного превышения;
- определить средние квадратичные ошибки единицы веса и среднего весового, оценить точность их определения;
- выполнить доверительное оценивание математического ожидания измеренной величины, дисперсии единицы веса и среднего квадратичного отклонения среднего весового при заданной доверительной вероятности β.
Порядок выполнения задания.
1. Значение веса измерения находится по формуле:
, (2.1)
где 
- дисперсия единицы веса,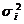 
- дисперсия измерения.
Дисперсия превышения определяется по формуле:
, (2.2)
Подставляя это выражение в формулу (2.1) получим выражение для вычисления веса превышения:
, (2.3)
где Li – длина хода нивелирования.
2. Определяем наиболее достоверное значение из ряда неравноточных измерений. Это среднее весовое или общая арифметическая средина, которую находим по формуле:
, (2.4)
где 
- сумма произведений измеренных значений на их веса, 
- сумма весов всех измерений.
Как и в предыдущей работе, вместо формулы (2.4) для определения среднего весового используют более удобную формулу
|
|
, (2.5)
где x о - условное значение, εi - вычисляют по формуле:
ε i = х і - х о, (2.6)
где х i - измеренное значение.
Чтобы не накапливать ошибки округления, среднее вычисляют с числом десятичных знаков хоть на один больше, чем в измеренных значениях х i.
2.Вычисляют отклонения измеренного значения х i от среднего весового
(2.7)
и выполняют 1 контроль
, (2.8)
где 
– предельная ошибка округления, равная 0,5 единицам последнего удерживаемого знака.
3.Вычисляют 
с контролем (2 контроль)
(2.9)
4. Определяют средние квадратические ошибки.
а) ошибку единицы веса по формуле Бесселя:
(2.10)
б) среднюю квадратичную ошибку среднего весового:
; (2.11)
в) среднюю квадратичную ошибку ошибки единицы веса:
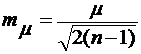; (2.12)
г) среднюю квадратичную ошибку средней квадратичной ошибки среднего весового:
(2.13)
5.Определяют доверительные интервалы для:
а) математического ожидания измерения
(2.14)
где параметр tβ выбирают из таблиц распределения Сьюдента (например, приложение V в [1] или приложения (2)) по заданной доверительной вероятности β и числу степеней свободы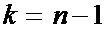 
;
б) дисперсии единицы веса:
(2.15)
в) среднего квадратичного отклонения среднего весового:
(2.16)
где μ и М средние квадратические ошибки, вычисленные по формулам (2.10) и (2.11). Коэффициенты γ1 и γ 2 выбирают из специальных таблиц по доверительной вероятности 
и по числу степеней свободы 
(приложение VIII в [l] или приложение (3)).
Пример. Приведенные результаты измерений превышений и длины семи секций нивелирования, последние выражены в км. По результатам измерений выполнить обработку ряда неравноточных измерений. Доверительные оценки получить с вероятностью 0,95.
|
|
Принимаем 
=3,120м
По формулам (2.3 – 2.13) вычисляем:
- общую арифметическую средину (среднее весовое)
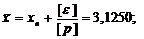
- среднюю квадратическую ошибку единицы веса:
- среднюю квадратическую ошибку ошибки единицы веса:
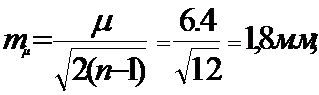
- среднюю квадратическую ошибку общей арифметической средины (среднего весового):
- среднюю квадратическую ошибку средней квадратичной ошибки
общей арифметической средины:
Сравним значения средних квадратических ошибок μ и M, и их средних квадратических ошибок mμ и mM. Из сравнения видно, что при исчислении средних квадратических ошибок достаточно оставлять две значащие цифры, при этом вторая цифра уже неточна.
Необходимые промежуточные вычисления и контроли приведены в таблице 2.1.
Таблица 2.1
| № | Превышение hi,м | Длина хода Li, км | Вес Рi | εi мм | Рεi мм | рεi2 мм2 | vi мм | рvi мм | рvi2 мм2 | Контроль |
| 3,117 | 1,083 | 0,92 | -3 | -2,77 | 8,310 | -8,05 | -7,436 | 59,8806 | ||
| 3,126 | 0,956 | 1,05 | 6,28 | 37,657 | 0,95 | 0,991 | 0,9381 | 1контроль | ||
| 3,135 | 1,066 | 0,94 | 14,07 | 211,069 | 9,95 | 9,331 | 92,8171 |  <0.03
| ||
| 3,130 | 1,250 | 0,80 | 8,00 | 80,000 | 4,95 | 3,958 | 19,5783 | 2контроль | ||
| 3,119 | 0,752 | 1,33 | -1 | -1,33 | 1,330 | -6,05 | -8,049 | 48,7217 | 243,1031= 243,103 | |
| 3,122 | 1,963 | 0,51 | 1,02 | 2,038 | -3,05 | -1,555 | 4,7482 | |||
| 3,131 | 2,154 | 0,46 | 5,11 | 56,175 | 5,95 | 2,761 | 16,4192 | |||
| Σ | 6,01 | 30,37 | 396,579 | 0,000 | 243,103 |
Строим доверительные интервалы:
а) доверительный интервал для математического ожидания измеренной величины. Значение tβ найдем по доверительной вероятности β = 0,95 по числу степеней свободы k = 7-1 = 6, по таблицам распределения Сьюдента из приложения (2), tβ = 2,6.
|
|
3,125м - 2,6 * 2,6мм< 
< 3,125м + 2,6 * 2,6мм
или
3,1182м< 
< 3,1318м
б) дисперсии единицы веса
Значения. γ1 и γ 2 найдем по доверительной вероятностью β = 0,95 и по числу степеней свободы k = 7-1 = 6, из таблиц приложения (3). Значения γ1 = 0,644 и γ 2 = 2,202.
6,7мм * 0,644 <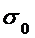 
< 6,7мм* 2,202,
или
28,9мм2 < 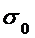< 98,4мм2
в) среднего квадратичного отклонения среднего весового
2,6мм * 0,644 < 
<2,6мм * 2,202
Или
1,67мм<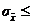 
5,72мм
Вывод по работе:
Наиболее достоверным значением измеренной величины является
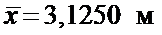
Его средняя квадратическая ошибка составляет
мм
Математическое ожидание измеренной величины с вероятностью 0,95 принадлежит интервалу
3,1182м< < 3,1318м
Приложения
Приложение 1
Таблица значений интеграла вероятностей
Ф(t)= 
| t | Φ(t) | t | Φ(t) | t | Φ(t) |
| 0,00 | 0,00000 | 1,25 | 0,78870 | 2,50 | 0,98758 |
| 0,05 | 0,03988 | 1,30 | 0,80640 | 2,55 | 0,98922 |
| 0,10 | 0,07966 | 1,35 | 0,82298 | 2,60 | 0,99068 |
| 0,15 | 0,11924 | 1,40 | 0,83849 | 2,65 | 0,99195 |
| 0,20 | 0,15852 | 1,45 | 0,85294 | 2,70 | 0,99307 |
| 0,25 | 0,19741 | 1,50 | 0,86639 | 2,75 | 0,99404 |
| 0,30 | 0,23582 | 1,55 | 0,87886 | 2,80 | 0,99489 |
| 0,35 | 0,27366 | 1,60 | 0,89040 | 2,85 | 0,99563 |
| 0,40 | 0,31084 | 1,65 | 2,90 | 0,99627 | |
| 0,45 | 0,34729 | 1,70 | 0,91087 | 2,95 | 0,99682 |
| 0,50 | 0,38292 | 1,75 | 0,91988 | 3,00 | 0,99730 |
| 0,55 | 0,41768 | 1,80 | 0,92814 | 3,10 | 0,99806 |
| 0,60 | 0,45149 | 1,85 | 0,93569 | 3,20 | 0,99863 |
| 0,65 | 0,48431 | 1,90 | 0,94257 | 3,30 | 0,99903 |
| 0,70 | 0,51607 | 1,95 | 0,94882 | 3,40 | 0,99933 |
| 0,75 | 0,54675 | 2,00 | 0,95450 | 3,50 | 0,99953 |
| 0,80 | 0,57629 | 2, 05 | 0,95904 | 3,60 | 0,99968 |
| 0,85 | 0,60468 | 2,10 | 0,96427 | 3,70 | 0,99978 |
| 0,90 | 0,63188 | 2,15 | 0,96844 | 3,80 | 0,99986 |
| 0,95 | 0,65789 | 2,20 | 0,97219 | 3,90 | 0,99990 |
| 1,00 | 0,68269 | 2,25 | 0,97555 | 4,00 | 0,99994 |
| 3,05 | 0,70628 | 2,30 | 0,97855 | 4,10 | 0,99996 |
| 1,10 | 0,72867 | 2,35 | 0,98123 | 4,20 | 0,99997 |
| 1,15 | 0,74986 | 2,40 | 0,98360 | 4,40 | 0,99999 |
| 1,20 | 0,76986 | 2,45 | 0,98571 | 4,50 | 0,999994 |
Приложение 2
Коэффициенты Сьюдента tβ
| Ф(t)=β | |||||||||||||
| r | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | 0.999 |
| 0,16 | 0,16 | 0,51 | 0,73 | 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | 636,6 | |
| 0,82 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | 31,6 | |||||
| 0.98 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | 12,9 | ||||||
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | 8,6 | |||||||
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | 6,9 | |||||||
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 | 6,0 | |||||||
| 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,5 | 5,4 | |||||||
| 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 | 5,0 | |||||||
| 1,1 | 1,4 | 1,8 | 2,3 | 2,8 | 3,3 | 4,8 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,8 | 3,2 | 4,6 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | 4,5 | |||||||
| 1,1 | 1,4 | 1,8 | 2,2 | 2,7 | 3,1 | 4,3 | |||||||
| 1,1 | 1.4 | 1,8 | 2,2 | 2,7 | 3,0 | 4,2 | |||||||
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 3,0 | 4,1 | |||||||
| 1,1 | 1,3 | 1,8 | 2,1 | 2,6 | 2,9 | 4,0 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | 4,0 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | 4,0 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,6 | 2,9 | 3,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,9 | 3,9 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,8 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1.7 | 2,1 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,5 | 2,8 | 3,7 | |||||||
| 1,1 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 | 3,6 | |||||||
| 1,0 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 | 3,5 | |||||||
| 1,0 | 1,3 | 1,7 | 2,0 | 2,4 | 2,6 | 3,4 | |||||||
| 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 2,6 | 3,3 |
Приложение 3
Коэффициенты γ1 и γ2
| г | 0,99 | 0,98 | 0,95 | 0,90 | ||||
| γ1 | γ2 | γ1 | γ2 | γ1 | γ2 | γ1 | γ2 | |
| 0,356 | 0,388 | 79,8 | 0,446 | 31,9 | 0,510 | 15,9 | ||
| O', 434 | 14,1 | 0,466 | 9,97 | 0,521 | 6,28 | 0,578 | 4,40 | |
| 0,483 | 6,47 | 0,514 | 5,11 | 0,566 | 3,73 | 0,620 | 2,92 | |
| 0,519 | 4,39 | 0,549 | 3,67 | 0,599 | 2,87 | 0,649 | 2,37 | |
| О; 546 | 3,48 | 0,576 | 3,00 | 0,624 | 2,45 | 0,672 | 2,090 | |
| 0,569 | 2,98 | 0,597 | 2,62 | 0,644 | 2,202 | 0,690 | 1,916 | |
| 0,588 | 2,66 | 0,616 | 2,377 | 0,661 | 2,035 | 0,705 | 1,797 | |
| 0,604 | 2,440 | 0,631 | 2,205 | 0,675 | 1,916 | 0,718 | 1,711 | |
| 0,618 | 2,277 | 0,644 | 2,076 | 0,688 | 1,826 | 0,729 | 1,645 | |
| 0,630 | 2,154 | 0,656 | 1,977 | 0,699 | 1,755 | 0,739 | 1,593 | |
| 0,641 | 2,056 | 0,667 | 1,898 | 0,708 | 1,698 | 0,748 | 1,550 | |
| 0,651 | 1,976 | 0,677 | 1,833 | 0,717 | 1,651 | 0,755 | 1,515 | |
| 0,660 | 1,910 | 0,685 | 1,779 | 0,725 | 1,611 | 0,762 | 1,485 | |
| 0,669 | 1,854 | 0,693 | 1,733 | 0,732 | 1,577 | 0,769 | 1,460 | |
| 0,676 | 1,806 | 0,700 | 1,694 | 0,739 | 1,548 | 0,775 | 1,437 | |
| 0,683 | 1,764 | 0,707 | 1,659 | 0,745 | 1,522 | 0,780 | 1,418 | |
| 0,690 | 1,727 | 0,713 | 1,629 | 0,750 | 1,499 | 0,785 | 1,400 | |
| 0,696 | 1,695 | 0,719 | 1,602 | 0,756 | 1,479 | 0,790 | 1,385 | |
| 0,702 | 1,666 | 0,725 | 1,578 | 0,760 | 1,460 | 0,794 | 1,370 | |
| 0,707 | 1,640 | 0,730 | 1,556 | 0,765 | 1,444 | 0,798 | 1,358 | |
| 0,712 | 1,617 | 0,734 | 1,536 | 0,769 | 1,429 | 0,802 | 1,346 | |
| 0,717 | 1,595 | 0,739 | 1,519 | 0,773 | 1,416 | 0,805 | 1,335 | |
| 0,722 | 1,576 | 0,743 | 1,502 | 0,777 | 1,402 | 0,809 | 1,326 | |
| 0,726 | 1,558 | 0,747 | 1,487 | 0,781 | 1,391 | 0,812 | 1,316 | |
| 0,730 | 1,541 | 0,751 | 1,473 | 0,784 | 1,380 | 0,815 | 1,308 | |
| 0,734 | 1,526 | 0,755 | 1,460 | 0,788 | 1,371 | 0,818 | 1,300 | |
| 0,737 | 1,512 | 0,758 | 1,448 | 0,791 | 1,361 | 0,820 | 1,293 | |
| 0,741 | 1,499 | 0,762 | 1,436 | 0,794 | 1,352 | 0,823 | 1,286 | |
| 0,744 | 1,487 | 0,765 | 1,426 | 0,796 | 1,344 | 0,825 | 1,279 | |
| 0,748 | 1,475 | 0,768 | 1,417 | 0,799 | 1,337 | 0,828 | 1,274 | |
| 0,774 | 1,390 | 0,792 | 1,344 | 0,821 | 1,279 | 0,847 | 1,228 | |
| 0,793 | 1,336 | 0,810 | 1,297 | 0,837 | 1,243 | 0,861 | 1,199 | |
| 0,808 | 1,299 | 0,824 | 1,265 | 0,849 | 1,217 | 0,871 | 1,179 | |
| 0,820 | 1,272 | 0,835 | 1,241 | 0,858 | 1,198 | 0,879 | 1,163 | |
| 0,829 | 1,250 | 0,844 | 1,222 | 0,866 | 1,183 | 0,886 | 1,151 | |
| 0,838 | 1,233 | 0,852 | 1,207 | 0,873 | 1,771 | 0,892 | 1,141 | |
| 0,845 | 1,219 | 0,858 | 1,195 | 0,878 | 1,161 | 0,897 | 1,133 | |
| 0,887 | 1,15 | 0,897 | 1,13 | 0,912 | 1,П | 0,925 | 1,09 |
Перечень ссылок
1.Большаков. В.Д., Маркузе Ю.И.Практикум по теории математической обработки геодезических измерений.– М.: Недра, 2007.-372с.