ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ
Виды погрешностей:
1. Погрешности модели
2. Погрешности исходных данных
3. Погрешности арифметических операций
Абсолютная и относительная погрешности
Введем обозначения. Пусть А - точное значение, а - приближенное значение.
Абсолютная погрешность (предельная)
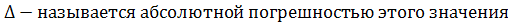
Докажем
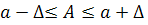
Относительная погрешность
Докажем
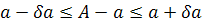
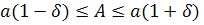
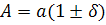
Цифры числа, начиная с первого ненулевого числа, слева называются значащими числа.
Значащую цифру называют верной или верной в узком смысле, если абсолютная погрешность числа меньше половины единицы разряда этой цифры.
Если абсолютная погрешность меньше единицы разряда этой цифры, то эта цифра называется верной в широком смысле.
Пример. Найти верные числа.
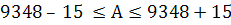
Обычно верные цифры пишут более крупно, а сомнительные мельче.
Ответ: 9348.
Пример. Найти относительную погрешность.
Ответ: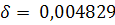 
.
ПОГРЕШНОСТИ ФУНКЦИЙ
Обозначим:
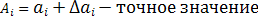
Тогда значение функции при точных значениях переменных будет выглядеть так: 
Абсолютная погрешность функции:
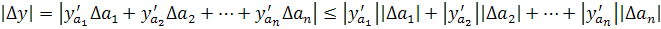
Пример.
Пример.
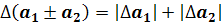
Пример.
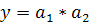
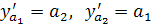
Абсолютная погрешность:
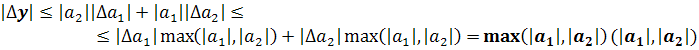
Вычислим относительную погрешность:
Относительная погрешность произведения равна сумме относительных погрешностей сомножителей.
Посчитаем относительную погрешность суммы и разности:
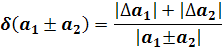
Вычислим относительную погрешность для степенной функции:
Пример.
Пример.
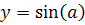
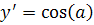
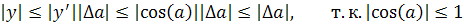
Пример.
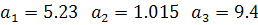
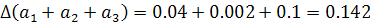
Вычислим верные числа в узком смысле: Проверим 15, 6 45 
0,1:2=0,05 < 0,142, значит 6 уже не верно в узком смысле.
15,645 – верны в узком смысле
15,645 – верны в широком смысле
Вычислим общую погрешность, после отбрасывания сомнительных цифр.
0,645+0,142=0,787 < 0,8
Пример.
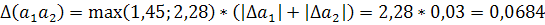
УПРОЩЕННЫЙ СПОСОБ ВЫДЕЛЕНИЯ ВЕРНЫХ И СОМНИТЕЛЬНЫХ ЦИФР
Правило подсчета цифр
При сложении и вычитании приближенных чисел в результате надо сохранять столько десятичных знаков после запятой, сколько их в приближенном, данном с наименьшим числом десятичных знаков.
Пример.
В произведении надо сохранить столько значащих цифр, сколько в сомнительном числе их с наименьшим количеством значащих цифр.
Пример.
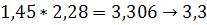
При возведении приближенных чисел в квадрат (куб) в результате надо оставлять столько значащих цифр, сколько их в основании.
Пример.
Пример.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ФУНКЦИЙ
Схема Горнера. Приближенное значение многочленов.
Предположим, что x-фиксированное число.
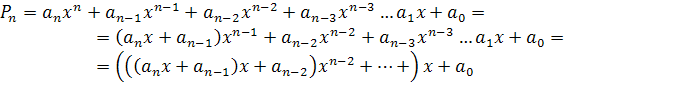
Пример.
…
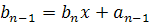
Задание. Используя схему Горнера, найти значение многочлена в точке x=0.5.
.
Проведем эту работу в SMathStudio.
Формула Тейлора.
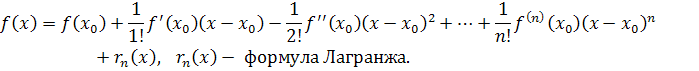
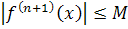
Пример.
Задание. Вычислить значения функций при заданных значениях аргумента методом разложения в ряд Тейлора с точностью до 10-6 . Провести эту работу в SMathStudio.
1) 
Воспользуемся разложением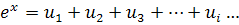 
, где 
, 
, i=1,2,3,…
2) 
Воспользуемся разложением 
, где
, 
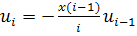, i=1,2,3,…
3) 
Воспользуемся разложением 
, где
, 
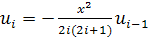, i=1,2,3,…
И разложением 
, где
, 
, i=1,2,3,…
ИНТЕРПОЛЯЦИЯ
Пусть нам даны точки 
на промежутке (a,b) и значения в этих точках 
Нам надо найти значения функции f(x), которые находятся между заданных значений. Если выполняются следующие условия:
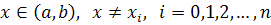, то такая операция называется интерполяция.
Если же x не принадлежит заданному промежутку, то операция называется экстраполяция.
Пример.
Вычислить температуру в промежуточный момент времени.
F(t)=T, t=t0, t1, …, tn
Если t>tn, то эта задача на прогнозирование, т.е. экстраполяции.
Пример.
Пусть нам даны две точки 
и значения в этих точках 
Тогда интерполирующая функция будет линейной, проходящей через две точки. Чтобы найти эту функцию воспользуемся формулой:
Проверим: 
Значит, 
является интерполирующим многочленом первой степени.
Пример.
Пусть нам даны три точки 
и значения в этих точках 
Тогда интерполирующая функция будет параболой, проходящей через три точки. Чтобы найти эту функцию воспользуемся формулой:
Проверим: 
Значит, является интерполирующим многочленом второй степени.
Пример.
Пусть нам даны n точек 
и значения в этих точках 
Тогда интерполирующей функцией, проходящей через n точек, будет:
Мы получили интерполяционный многочлен Лагранжа.
Задание. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа и построить график, если функция задана:
y(0.115)=8.65729, y(0.215)=8.29329, y(0.315)=7.95829, y(0.415)=7.64893, y(0.515)=7.36235, y(0.615)=7.09613
Вычислить в точке: x=0.35
Провести эту работу в SMathStudio.
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
Остановимся отдельно на простейшем виде локального аналитического приближения таблиц, которым является линейное интерполирование. Во-первых, во многих случаях его вполне достаточно для вычисления значений табличных функций, особенно математических. Во-вторых, в этом случае можно дать простое правило определения верных значащих цифр приближенного значения функции непосредственно по свойствам исходной таблицы, без вычисления абсолютной погрешности этого значения.
Пример.
Пусть нам даны точки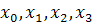 
и значения в этих точках 
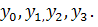Тогда мы можем построить график этой функции с помощью сумм отрезков по формуле y=kx+b, образующий ломаную.
ИНТЕРПОЛЯЦИЯ СПЛАЙНА
Интерполяция сплайна отличается тем, что вместо прямых мы используем параболы.
Задание. Найти приближенное значение функции при данном значении аргумента с помощью линейной интерполяции и построить график.
Провести эту работу в SMathStudio.
ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА
Пусть нам даны точки на промежутке (a,b) и значения в этих точках Нам надо найти значения функции g(x), которые находятся между заданных значений. Если выполняются следующие условия:
, функция должна быть интерполирующей.
Выберем интервал: 
В качестве интерполирующий функций удобно брать: 
Возьмем частичную сумму ряда Фурье:
В этом выражении количество неопределенных коэффициентов равно 2n+1. Чтобы их найти нам надо 2n+1 условие. Тогда: 
Интерполяционный многочлен Лагранжа:
Выпишем интерполяционный многочлен Лагранжа первой степени:
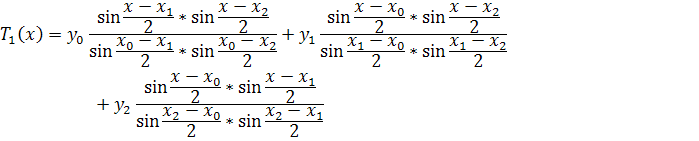
Задание. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена тригонометрической функции и построить график.
Провести эту работу в SMathStudio.
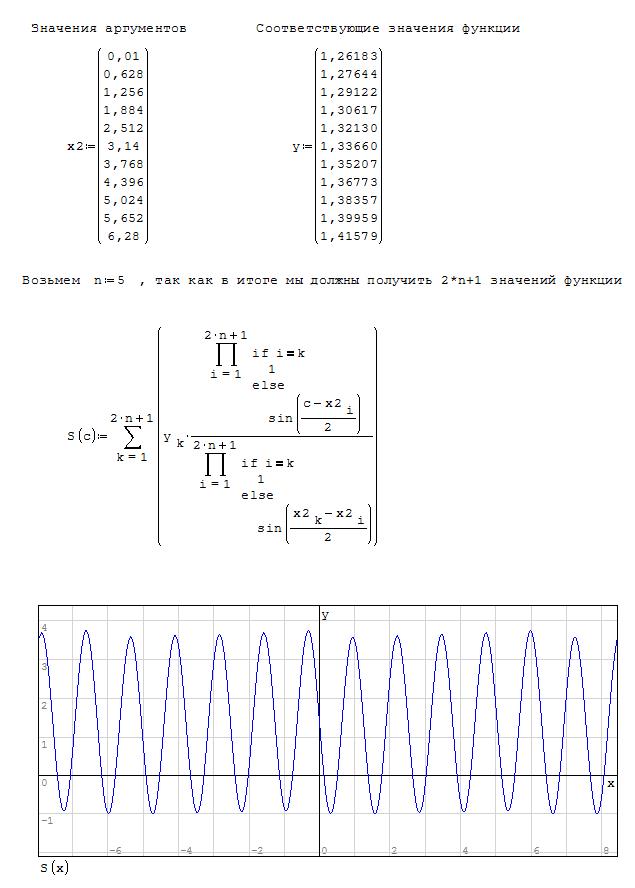
Рассмотрим промежуток 
.
В этом случае функция будет четная. Точки будут располагаться только справа от нуля. Следовательно, нам понадобится n+1 точка. Тогда многочлен четной тригонометрической функции будет выглядеть:
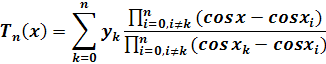
Задание. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного четного многочлена тригонометрической функции и построить график.
Провести эту работу в SMathStudio.
Рассмотрим промежуток 
.
Многочлен нечетной тригонометрической функции будет выглядеть:
Задание. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного нечетного многочлена тригонометрической функции и построить график.
Провести эту работу в SMathStudio.
АППРОКСИМАЦИЯ ФУНКЦИЙ
Изначально задаются точки 
и значения фуекции в этих точках Пусть заданы функции 
– базисные функции, причем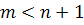 
. В простейшем случае 
может быть одна. Построим из них линейную комбинацию.
Для решения этой задачи надо подобрать коэффициенты.
Если бы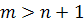 
, то система была бы не доопределена; если 
, то решение системы зависит от определителей (если определитель не равен нулю, то система имеет решение); если 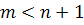, то количество неизвестных меньше, чем количество уравнений и такая система будет переопределена.
Пример.
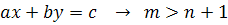, система не доопределена.
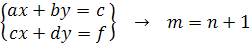, решение системы зависит от определителей.
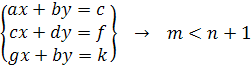, система переопределена.
Для решения переопределенной системы нам надо, чтобы система была линейно зависима. Если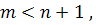 
то уравнение (1) маловероятно решить. Тогда надо переходить от задачи интерполяции к задаче аппроксимации:
Нам надо устремить эту разность к нулю. Для этого:
Ставится задача минимизировать эту функцию по коэффициентам 
. Если подставим, то получим:
Эта функция является квадратичной, т.е. функция похожа на параболу или параболоид (если несколько переменных). Если посчитать, то мы можем найти min. Чтобы его найти, надо посчитать частную производную и приравнять ее к нулю.
- коэффициенты при неизвестных,
- свободные члены.
Получили линейную систему:
Этот метод называется методом наименьших квадратов.
Рассмотрим несколько примеров.
Даны функции 
Пусть m=1.
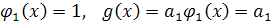
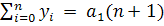
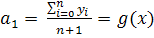– мы получили среднеарифметическое.
Аппроксимация этой функции.
Пример.
По правилу Крамера:
Найдем коэффициенты:
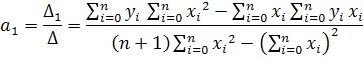
Задание. Найти аппроксимирующую прямую для функции, заданной графиком, построить линейную интерполяцию и сравнить получившиеся функции на графике.
Провести эту работу в SMathStudio.
