Задана функция с значениями в n+1 точке, и значения функции y в этих точках:
Надо численно посчитать производную в этих точках с 
и в промежутках между ними.
Существует несколько способов:
1. Написать интерполирующую функцию и вычислить от нее производную.
2. Использовать конечные разности.
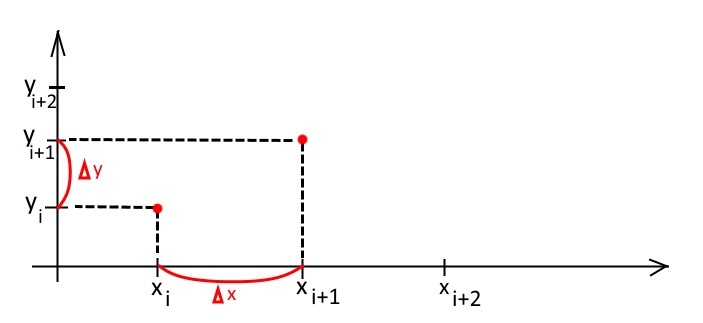
Найдем приращения функции:
Вычислим производную:
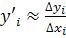, здесь 
- конечные разности, 
- разделенные разности.
Для вычисления второй производной нам понадобятся три точки.
- приращение производной.
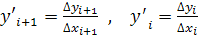
- вторая производная.
Предположим, что расстояние между точками одинаково и равно h.
Тогда вторая производная равна:
Задание. Используя конечные разности найти линейную интерполяцию функции, вычислить и построить график интерполяционного многочлена Лагранжа, найти производную от многочлена Лагранжа и сравнить график с графиком, построенным с помощью конечно-разностных приращений, найти вторую производную от многочлена Лагранжа.
Провести эту работу в SMathStudio.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Формулы левых и правых прямоугольников.
Для вычислений по формулам левых и правых прямоугольников с шагом n надо разбить отрезок интегрирования на n частей с шагом h.
Найдем значения сумм:
Найдем приближенные значения интеграла. По формуле левых прямоугольников получим:
По формуле правых прямоугольников находим
Эти результаты мало отличаются. За окончательное значение примем полусумму найденных значений:
Формула средних прямоугольников.
Для решения воспользуемся формулой средних прямоугольников:
Для вычислений по формуле средних прямоугольников с шагом n надо разбить отрезок интегрирования на n частей с шагом h.
Вычислим суммы подынтегральной функции в заданных точках. Найдем приближенное значение интеграла:
Задание. 1) Вычислить интеграл по формулам левых и правых прямоугольников при n=10, оценивая точность с помощью сравнения полученных результатов. 2) Вычислить интеграл по формуле средних прямоугольников, используя для оценки точности двойной просчет при 
.
Провести эту работу в SMathStudio.
Формула трапеции.
Чтобы вычислить интеграл по формуле трапеции надо использовать формулу:
Задание. Вычислить интеграл по формуле трапеций.
Провести эту работу в SMathStudio.
Формула Симпсона.
Чтобы вычислить интеграл по формуле Симпсона с заданным шагом n нам надо разбить наш интервал интегрирования на n шагов.
Формула симпсона имеет вид:
Задание. Вычислить интеграл по формуле Симпсона при n = 8.
Провести эту работу в SMathStudio.
Метод Гаусса.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Задание. Используя схему Гаусса, решить систему уравнений.
Провести эту работу в SMathStudio.
Метод Крамера.
Метод Крамера — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы. Назван по имени Габриэля Крамера, автора метод.
Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:
где 
- определитель матрицы системы, 
- определитель матрицы системы, где вместо i -го столбца стоит столбец правых частей.
Задание. Используя метод Крамера, решить систему уравнений.
Провести эту работу в SMathStudio.
