У р а в н е н и е А р р е н и у с а. Скорость химических реакций обычно сильно зависит от температуры. Так, по правилу Вант - Гоффа для реакций в растворах при повышении температуры на десять градусов скорость увеличивается в 2-3 раза.
 2 -4; r(T2)/r(T1) =
2 -4; r(T2)/r(T1) = 
Математически зависимость константы скорости от температуры выражается экспоненциальным уравнением Аррениуса k = А × exp (-Ea/RT) (8), где
А – предэкспоненциальный множитель или экспонента, Еa - энергией активации.
В логарифмической форме уравнение Аррениуса принимает линейную форму от обратной температуры
ln k = ln A −  (9)
(9)
Параметры уравнения Аррениуса определяются экспериментально при изучении температурной зависимости константы скорости. Если имеются значения константы скорости при двух температурах, то энергия активации рассчитывается по формуле
 (10)
(10)
При большем количестве опытных точек, строят график зависимости ln k = f(1/T), угловой коэффициент наклона которого равен tga = - Е/R в соответствии с уравнением (9). Так как температурный интервал экспериментальных данных обычно не превышает нескольких десятков градусов, графическое определение предэкспонента А затруднено из-за необходимости далекой экстраполяции. Поэтому величину А рассчитывают аналитически из уравнения 8, используя экспериментальные значения k при разных температурах и найденное значение энергии активации.
П р и м е р 5.
Для реакции йодистого этила с алкоголятом натрия в этиловом спирте
CH3I + C2H5O- = CH3OC2H5 + I-
найдены следующие значения константы скорости второго порядка
| t, 0C | |||||
| k×105, л/(мол××с) | 5,00 | 11,8 | 24,5 | 48,8 |
Определить энергию активации реакции и предэкспоненциальный множитель уравнения Аррениуса, рассчитать константу скорости при 15 о С.
Решение. Рассчитаем необходимые для построения графика 2.2 величины
| T, K | |||||
| T-1×103, К- 1 | 3,663 | 3,584 | 3,508 | 3,436 | 3,367 |
| ln k | 1,609 | 2,468 | 3,199 | 3,888 | 4,605 |
(Обращаем Ваше внимание на то, что при расчете величин 1/T нужна учитывать третий знак после запятой, так как область изменения аргумента составляет всего 0,3 единицы и в противном случае точность определения искомой величины не будет соответствовать точности экспериментальных данных)
Построим график ln k - 1/T и найдем угловой коэффициент его наклона (рис. 2.1)
из уравнения прямой, полученной после обработки: y = 26,8326 – 10020,76*x
|
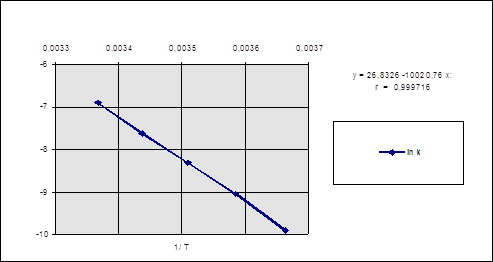
Рис. 2.1. Зависимость логарифма константы скорости реакции от обратной температуры.
Полученное уравнение прямой сравним с уравнением Аррениуса:
y = 26,8326 – 10020,76*x
ln k = ln A −  , отсюда видно, что при y = ln k, х = 1/T
, отсюда видно, что при y = ln k, х = 1/T
tga =-Ea/R = - 10020,76 lnA = 26,8326.
Найдем активационные параметры:
E = - R × tg a = 8,314 Дж/(моль×К) ×10,02×103 К = 83306 Дж/моль = 83,3 кДж/моль.
lnA = 26,8326; А = 4, 50 ×1011 л/(моль×с)
Можно использовать также значение свободного члена в регрессионном уравнении. Отсюда А = 4, 50 ×1011 л/(моль×с)
Используя найденные параметры уравнения Аррениуса можно определить константу скорости данной реакции при любой температуре в рабочем интервале, например при 15оС
k15 =4,50×1011× exp [-83300/(8,314×288)]= 4,50 ×1011 ×7,786 ×10-16 =
=35,0.10-5 л/(моль.с)
Для аналитического расчета можно воспользоваться формулой для двух температур:

Для расчета предэкспонента используем значение k при любой температуре, если точка хорошо лежит на графике.
ln А = ln k + E/RT = - 6,905 + 10020/297 = - 6,905+33737 =26,83.
Для контроля за расчетами примем следующие ориентиры:
Среднее значение Ea = 80 – 120 кДж/моль
Для нормальной реакции: (понятие нормальной реакции уточним позже)
При n=1; A = 109 c-1
При n=2; A = 1011-1012 л /моль*с
Размерность предэкспоненты полностью совпадает с размерностью константы скорости для каждого порядка