В парном регрессионном анализе эквивалентны t -критерий для H 0: β = 0, t -критерий для H 0: r = 0, F -критерий для R 2, т.е.
.
Связь между критериями выражается равенством
,
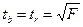причем для критических значений критериев при любом уровне значимости имеем:
и эти критерии дают один и тот же результат.
Вывод. Проверки значимости коэффициента b в парной линейной регрессии, коэффициента корреляции r и коэффициента детерминации R 2 эквивалентны.
3.4. Прогнозирование в регрессионных моделях.
Под прогнозированием в эконометрике понимается построение оценки зависимой переменной для некоторого набора независимых переменных, которых нет в исходных наблюдениях.
Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, во втором – интервал, в котором находится истинное значение зависимой переменной с заданным уровнем значимости.
Рассмотрим регрессионную модель:
y = a + bx + e.
Действительное значение зависимой переменной при x = xр есть:
yр = a + bxр + eр,
где значения a, b, eр неизвестны и M(eр) = 0, D (eр) = s 2.
Предсказанным значением является оценка yр (точечный прогноз):
Ошибка предсказания равна разности между предсказанным и действительным значениями:
.
Ошибка предсказания имеет нулевое математическое ожидание:
M( D р) = 0.
Действительно,
.
Вычислим дисперсию прогноза. Учитывая, что в случае парной регрессии
,
для дисперсии прогноза получим:
Из формулы следует, что чем больше xр отклоняется от выборочного среднего `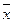 
, тем больше дисперсия ошибки предсказания, и чем больше объем выборки n, тем меньше дисперсия.
Заменяя в дисперсии прогноза s 2 на её оценку S 2и извлекая квадратный корень, получим стандартную ошибку предсказания:
|
|
.
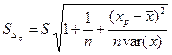Доверительный интервал для действительного значения yр определяется выражением:
,
где tкр . – критическое значение t -статистики при заданном уровне значимости и числе степени свободы.
На рис. 11 в общем виде показано соотношение между доверительным интервалом предсказания и значением объясняющей переменной.
Отрезок, помеченный на рис. 11 стрелками, определяет доверительный интервал предсказания в точке хр.
Рис. 11
Пример. 3.7. По данным объема продаж y фирмы от затрат x на рекламу оценить объем продаж при затратах на рекламу равной 5,5 усл. ед. Найти стандартную ошибку предсказания и 99 %-ный доверительный интервал для полученной оценки.
Исходные данные (усл. ед.):
| x | ||||||||||
| y |
Объем продаж фирмы yp = 71,87 призатратах на рекламу xp = 5,5 можно определить с помощью статистической функции Excel:
yp = ПРЕДСКАЗ (xp, массив х, массив у)[3].
Значения 
можно получить с помощью функций:
= СРЗНАЧ (массив х);
var(x) = ДИСП (массив х);
S = СТОШУХ (массив у, массив х);
tкр = СТЬЮДРАСПОБР (a, ν);
где n = 10, ν = n – 2 = 8, α = 1 – 0,99 = 0,01.
Вычисляем стандартную ошибку предсказания и доверительный интервал для полученной оценки:
,
или 
.
Нелинейные регрессии
Нелинейность регрессии проявляется как по переменным, так и по параметрам.
Нелинейность по переменным устраняется путем замены переменной. Например, нелинейное уравнение 
после замены переменной 
становится линейным: y = a + bz + e и для оценки ее параметров используется МНК.
|
|
Пример. 3.8. Имеются данные между ежегодным потреблением бананов (y) и годовым доходом (x) 10 американских семей (усл. ед.):
| X | ||||||||||
| Y |
Рассмотрим различные варианты уравнения регрессии.
1). Оценка линейного уравнения y = a + b x + e по выборочным наблюдениям (y, x) приводит к уравнению:
.
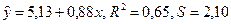2). Если рассмотрим нелинейное уравнение 
и определим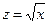 
, то уравнение примет линейный вид y = a + b z + e.
Оценив регрессию между y и z, получим:
.
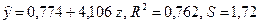Подставив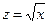 
, имеем: 
.
3). Если рассмотрим нелинейное уравнение y = a + b / x + e, и определим z = 1/ x, то уравнение примет линейный вид y = a + b z + e.
Оценив регрессию между y и z, получим:
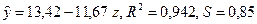
Подставив z = 1/ x, имеем: 
.
Качество оценивания последнего варианта уравнения выше других.
В таблице представлены исходные данные для построения рассмотренных уравнений регрессии с помощью пакета анализа Excel(Регрессия).
| y | x |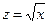
| z = 1/ x |
| 1,414 | 0,5 | ||
| 1,732 | 0,333 | ||
| 0,25 | |||
| 2,236 | 0,2 | ||
| 2,449 | 0,166 | ||
| 2,645 | 0,142 | ||
| 2,828 | 0,125 | ||
| 0,111 | |||
| 3,162 | 0,1 |
Нелинейность по параметру часто устраняется путем логарифмического преобразования.
Например, следующие нелинейные (мультипликативные) уравнения после логарифмирования сводятся к линейным:
- степенная функция y = axbe ~ ln y = ln a + bln x + ln e;
- экспоненциальная функция y = aebxe ~ ln y = ln a + b x + ln e.
Использование МНК для нахождения оценок параметров этих уравнений требует, чтобы ln e имел нормальное распределение.
|
|
Однако, уравнение y = axb + e, в котором случайный член e является аддитивным, уже никакими преобразованиями не приводится к линейному.
В этом случае используют специальные итерационные методы оценивания нелинейной регрессии.
В экономике функции вида 
применяются при моделировании кривых спроса, а вида y = a ebx e – при моделировании временных трендов, при этом вместо x используется время t, а вместо b – постоянный темп прироста r, то есть, y = a ert e.
Пример. 3.9. По данным примера 2.5 построим зависимость расходов на питание от доходов в виде степенной функции и экспоненциальный временной тренд.
В таблице представлены исходные данные для построения указанных уравнений с помощью пакета анализа Excel(Регрессия).
| T | x | Y | ln x | ln y |
| 0,69314 | ||||
| 1,79175 | 0,69314 | |||
| 2,30258 | 1,38629 | |||
| 2,63905 | 2,39789 | |||
| 2,89037 | 2,48490 |
1). Уравнение y = axbe после логарифмирования приводится к линейному виду ln y = ln a + b ln x + ln e.
Оценив регрессию между ln y и ln x, получим преобразованное выражение:
.
Выполнив обратные преобразования, получим:
.
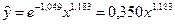2). Уравнение y = a ert e после логарифмированияприводится к линейному виду ln y = ln a + rt + ln e.
Оценив регрессию между ln y и t, получим преобразованное выражение:
.
Выполнив обратные преобразования, получим:
В экономическом анализе часто используется эластичность функции.
Эластичность функции y = f (x) рассчитывается как относительное изменение y к относительному изменению x, то есть:
.
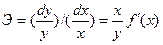Эластичность функции показывает, на сколько процентов изменяется функция y = f (x)при изменении независимой переменной на 1 %.
Для степенной функции 
эластичность представляет собой постоянную величину, равную b.
Например, для зависимости расходов на питание от дохода 
эластичность спроса на продукты питания по доходу составляет 1,183.
Это означает, что увеличение личного дохода на 1 % приведет к увеличению расходов на питание на 1,183%.
Коэффициент 0,350 не имеет простого толкования. Он помогает прогнозировать значение y при заданных значениях x, приводя их к единому масштабу.
Для экспоненциального временного тренда 
постоянный темп роста r = 0,667. Это означает, что расходы на продукты питания в течение выборочного периода росли с темпом 66,7 % в год.
Постоянный множитель 0,543 показывает, что в момент t = 0 общие расходы на питания составили 0,543 усл. ед.
В силу того, что эластичность линейной функции y = a + bx не является постоянной величиной, а зависит от x, то есть
,
то обычно рассчитывается средний показатель эластичности по формуле:
,
где 
– средние значения переменных x, y в выборке.
Например, для зависимости расходов на питание от доходов 
, 
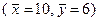средний показатель эластичности 1,29 показывает, что с увеличением дохода на 1 % расходы на питание возрастут в среднем на 1,29 %.
[1] СТЬЮДЕНТ.РАСП.2Х
[2] СТЬЮДЕНТ.ОБР.2Х
[3] ПРЕДСКАЗ.ЛИНЕЙН