Полученные теоретические дисперсии D (a), D (b) зависят от дисперсии s 2 случайного члена.
По данным выборки отклонения ei, а, следовательно, и их дисперсии s 2неизвестны, поэтому они заменяются наблюдаемыми остатками ei и их выборочной дисперсией var(e).
Но оценка var(e) является смещенной, т.е.
.
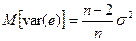Несмещенной оценкой дисперсии s 2 является величина (остаточная дисперсия):
,
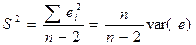которая служит мерой разброса зависимой переменной вокруг линии регрессии.
Отметим, что в знаменателе остаточной дисперсии стоит число степеней свободы (n – 2), а не n, так как две степени свободы теряются при определении двух параметров (a; b).
Величина S называется стандартной ошибкой регрессии.
Заменив в теоретических дисперсиях неизвестную s 2 на оценку S 2, получим оценки дисперсий:
.
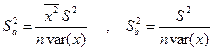Величины Sa, Sb называется стандартными ошибками коэффициентов регрессии.
Пример 3.1. По полученным в примере 2.5 результатам при определении зависимости расходов на питание от личного дохода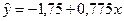 
рассчитать стандартные ошибки коэффициентов регрессии.
Исходные данные: n = 5, var(x) = 32, 
= 132, var(e) = 1,98.
Остаточная дисперсия S2 и стандартная ошибка регрессии S есть:
, 
.
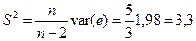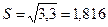Для расчета стандартной ошибки можно также воспользоваться функцией Excel:
S = СТОШYX (массив Y; массив X).
Стандартные ошибки коэффициентов регрессии:
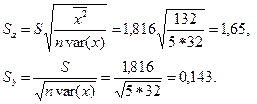
Пример 3.2. Покажем, что в выборочной регрессии без свободного члена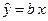 
стандартная ошибка оценки b есть:
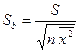, где 
.
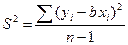Подставим в оценку для b выражение 
, получим:
.
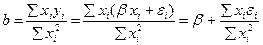Оценка b является несмещенной, т.к.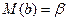 
.
Дисперсия оценки b есть:
.
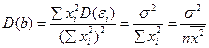В исходной модели оценивается один параметр, поэтому оценкой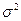 
является 
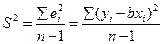, следовательно, .
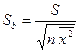Пример 3.3. Покажем, что в выборочной регрессии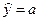 
стандартная ошибка оценки a есть
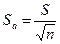, где 
.
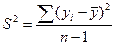Подставим в оценку для a выражение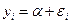 
, получим:
.
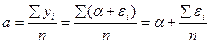Оценка a является несмещенной, т.к.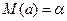 
.
Дисперсия оценки a есть:
.
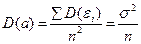В исходной модели оценивается один параметр, поэтому оценка :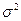
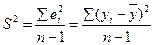, следовательно, 
.
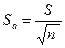Пример 3.4. По данным примера 2.5. построим зависимость расходов на питание y от личного дохода x для модели регрессии без свободного члена и рассчитаем стандартную ошибку коэффициента регрессии.
Исходные данные и расчетные показатели представим в таблице.
| Год | x | y | x2 | Xy | 
| 
| 
| 
|
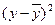
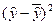
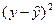
| 1,28 | 26,378 | 0,0806 | ||||||
| 3,85 | 6,594 | 3,429 | ||||||
| 6,42 | 5,856 | |||||||
| 8,99 | 6,594 | 4,048 | ||||||
| 11,56 | 26,378 | 0,193 | ||||||
| Итого | 32,1 | 65,946 | 13,608 | |||||
| Среднее | 84,8 | 6,42 | 21,2 | 13,189 | 2,721 | |||
| 
| 
| 
| 
| 
| 
| 
|
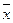
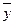
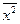
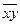
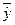
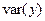
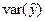
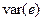
Коэффициент b определяется выражением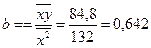 
, следовательно, 
.
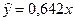Заметим, что в отсутствии свободного члена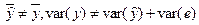 
.
Остаточная дисперсия S 2и стандартная ошибка регрессии S равны: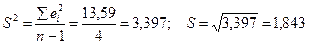 
.
Стандартная ошибка коэффициента регрессии равна:
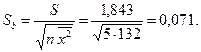
Статистические свойства МНК-оценок (a; b)
Пусть выполняется условие нормальности распределения случайного члена: eI ~ N (0; s 2). Тогда МНК-оценки коэффициентов регрессии также имеют нормальное распределение, поскольку являются линейными функциями от ei, т.е.
;
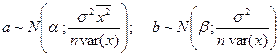Если условие нормальности распределения случайного члена не выполняется, то оценки (a; b) имеют асимптотически нормальное распределение.
3.3. Проверка гипотез, относящихся к коэффициентам регрессии (a; b).
Проверка гипотезы H0: b = b 0.
Пусть в теоретической зависимости Y = a + b X + e случайный член e распределен нормально с неизвестной дисперсией s 2.
Величина b хотя и неизвестна, но имеется основание предполагать, что она равна заданной величине b 0.
Выдвигаются гипотезы:
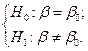
Задача заключается в проверке нулевой гипотезы на основании выборочных данных.
Пусть по выборочным данным получена оценка b.
В качестве критерия проверки нулевой гипотезы принимают случайную величину:
,
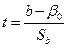которая имеет распределение Стьюдента с n = n – 2 степенями свободы.
По таблице критических точек распределения Стьюдента по заданному уровню значимости a и числу n степеней свободы находят критическую точку t кр.
Сравнивая наблюдаемое значение критерия с критическим, можно принять или отвергнуть нулевую гипотезу.
Результаты оценивания регрессии совместимы не только с конкретной гипотезой H 0: b = b 0, но и с некоторым их множеством.
Любое значение b, совместимое с оценкой b, удовлетворяет условию
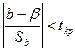, или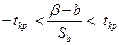 
.
Разрешив это неравенство относительно b получим:
b – t кр Sb < b < b + t кр Sb,
т.е. доверительный интервал для величины b.
Посредине интервала лежит величина b. Границы интервала одинаково отстоят от b, зависят от выбора уровня значимости и являются случайными числами.
Доверительный интервал покрывает значение параметра b с заданной вероятностью (1 – a), т.е.
P (b – t кр Sb < b < b + t кр Sb) = 1 – a.
Проверка гипотезы H 0: b = 0
Пусть по выборке получена оценка коэффициента регрессии b.
Для определения статистической значимости коэффициента регрессии b проверяется гипотеза H 0: b = 0 для t- статистики, рассчитываемой по формуле 
.
Величина t имеетраспределение Стьюдента с n = n – 2 степенями свободы.
Наблюдаемому (расчетному) значению критерия t соответствует определенная значимость t, которую можно определить в Excel с помощью функции:
Значимость t = CТЬЮДРАСП (t; n; 2).
Из сравнения значимости t с заданным стандартным уровнем значимости, получаем:
- если значимость t > стандартного уровня, то b незначим;
- если значимость t <стандартного уровня, то b значим.
Пример 3.5. Зависимость расходов на питание от личного дохода по данным примера 2.5 имеет вид (в скобках указаны стандартные ошибки):
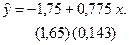
Оценим значимость коэффициента регрессии b = 0,775 и построим доверительный интервал для b при уровне значимости 5 %.
Наблюдаемое значение критерия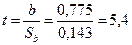 
.
Значимость t = 0,0124, соответствующая расчетному значению критерия t = 5,4, определяем с помощью функции: значимость t = СТЬЮДРАСП(t; n; 2)[1], где n = 3. Поскольку значимость t = 0,0124 < 0,05, то коэффициент регрессии b =0,775 значим.
При a = 0,05 критическое значение критерия t кр= 3,18 определяем с помощью функции: t кр=СТЬЮДРАСПОБР(a; n)[2].
Доверительный интервал для b есть:
0,775 – 3,18×0,143 < b < 0,775 + 3,18×0,143 или 0,32 < b < 1,23.