Изучить по учебной литературе вопросы:
1. Неопределенный интеграл: определение, свойства, таблица интегралов. 
2. Способы вычисления неопределенного интеграла: непосредственное интегрирование, способ подстановки.
3. Определенный интеграл: определение, свойства, геометрический смысл.
4. Способы вычисления определенного интеграла.
5. Применение определенного интеграла к решению практических задач: вычисление площадей плоских фигур.
| 1.Основные правила интегрирования |
1. Если  то то  где где  – произвольная постоянная.
2. – произвольная постоянная.
2.  где где  – постоянная.
3. – постоянная.
3. 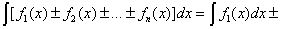

|
| 2.Таблица основных неопределенных интегралов |
1.  .
2. .
2.  3.
3.  .
4. .
4.  5.
5.  6.
6. 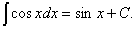 7.
7.  8.
8.  9.
9. 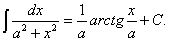 10.
10.  11.
11.  12.
12.  
|
| 3.Непосредственное интегрирование |
Отыскание неопределенного интеграла с помощью таблицы, правил и тождественных преобразований называют непосредственным интегрированием.
Пример:
  - -  + +  )dx = 2 )dx = 2  dx - dx -   dx - dx -  dx + 3 dx + 3  = 2 = 2  - -  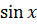 +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11. +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11.
|
| 4.Метод подстановки (замена переменной интегрирования) |
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а)  где где  – монотонная, дифференцируемая функция; б) – монотонная, дифференцируемая функция; б)  – новая переменная.
В первом случае формула замены переменной имеет вид: – новая переменная.
В первом случае формула замены переменной имеет вид:
 . (1)
Во втором случае: . (1)
Во втором случае:
 . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл: . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл:
 Решение.
Сделаем замену переменных t=x+1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
Решение.
Сделаем замену переменных t=x+1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
 = =  = =  +C = +C =  +C,
где C - const. Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ. +C,
где C - const. Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.
|
Пример 2:
 (положим t = 2x+3, тогда x=
(положим t = 2x+3, тогда x=  t-
t-  , dx =
, dx =  dt)
dt)
= 
 =-
=- 
 +C= =-
+C= =- 
 +C
+C
Пример 3:
 dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=
dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=  dt) =
dt) =  *
*  dt=
dt=  dt=
dt= 
 +C =
+C = 
 +C =
+C = 
 +C =
+C = 
 +C
+C
Определенный интеграл.
Если существует определенный интеграл от функции f(x), то в этом случае функция называется интегрируемой на отрезке  .
.
Для интегрируемости функции на отрезке  достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
Если функция непрерывна на  , то от нее существует неопределенный интеграл
, то от нее существует неопределенный интеграл
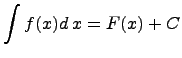
и имеет место формула

т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.
Формула

называется формулой Ньютона-Лейбница.
Пример 1:
Необходимо найти определенный интеграл

Имеем:

Таким образом искомый интеграл равен 6.
Пример 2:
Вычислить интеграл: 
Решение:
 =(3
=(3  + 4
+ 4  +5x)
+5x)  =
=  +2
+2  -
-
- ( +2
+2  26- 8=18.
26- 8=18.
Примеры решения задач
1) Найти неопределенные интегралы:

Решение
При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
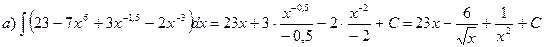
б) Выполнив почленное деление в подынтегральной функции, получим:

в)

г) Будем использовать подстановку:

д) Воспользуемся подстановкой:

2) Вычислить определенные интегралы:

Решение
При вычислении определенных интегралов используем формулу Ньютона-Лейбница
 . Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.




3. Найти площадь фигуры, ограниченной линиями: у=1 – х2 + 4х и 2х – у – 2 =0
Для определения точек пересечения линий составим уравнение из равенства выражений этих линий: 1 – х2 + 4х = 2х – 2; получим уравнение: х2 – 2х – 3 = 0.
Корнями этого уравнения являются числа: (-1) и 3. Для построения линий найдем
значения функций и составим их таблицы:
| х | -1 | х | -1 | ||||||
| у1 | -4 | у2 | -4 |
Построив фигуру на плоскости, вычислим ее площадь, определив значение интеграла

