Формы записи законов управления в виде дифференциальных уравнений

9) Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

12) Стандартная форма записи линейных уравнений
В общем виде линеаризованное дифференциальное уравнение одномерного элемента можно представить в виде (2.1):

(2.1)

, где y(t), x(t), f(t) - выходная, входная и возмущающее величины элемента или системы (в отклонения от состояния равновесия);a_i, b_i, c_i - постоянные коэффициенты;
n - порядок уравнения, при этом n≥m - условие физической реализуемости элемента.

Для удобства и формализации решений уравнение (2.1) может быть пред-ставлено в одной из пяти стандартных форм:
1. в форме Коши;
2. в пространстве состояний;
3. в виде передаточных функций - W(p), Φ(p), Φ_ε(p).
4. решение относительно регулируемой величины - y(t);
5. решение относительно ошибки - Δ(t);
13-14) Структурное схематическое представление законов управления

Преобразования структурных схем. Структурная схема системы в простейшем случае строится из элементарных динамических звеньев. Несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем.

Последовательное соединение (рис. 2.5.1) - выходная величина предшествующего звена подается на вход последующего. При этом можно записать:

Рис. 2.5.1.

y₁ = W₁ y₀; y₂ = W₂ y₁;...; y_n = W_n y_n-1,

y_n = W₁ W₂...W_n y₀ = W_экв y₀.

W_экв = W_i.

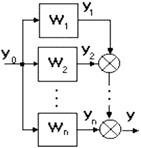Рис. 2.5.2.

Передаточные функции последовательно соединенных звеньев перемножаются.

Параллельное соединение (рис.2.5.2) - на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются:

y = y₁ + y₂ +... + y_n = (W₁ + W₂ +... + W_n) y₀ = W_экв y₀.

W_экв = W_i.

Рис. 2.5.3.

Цепочка звеньев, соединенных параллельно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев.

Замкнутое соединение с обратной связью (рис. 2.5.3а) - звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет с выхода на вход, называется цепью обратной связи с передаточной функцией W_ос. Для отрицательной обратной связи (ОС):

y = W_п u; y₁ = W_ос y; u = y₀ - y₁,

y= W_п y₀ - W_п y₁ = W_п y₀ - W_п W_oc y = y(1+W_п W_oc) = W_п y₀ = W_экв y₀,

W_экв = W_п /(1+W_п W_ос).

Для положительной ОС:

W_экв = W_п /(1-W_п W_ос).

Если W_oc = 1, то обратная связь называется единичной (рис. 2.5.3б):

W_экв = W_п /(1 ± W_п).

Рис. 2.5.4.

Как прямая W_п, так и обратная W_ос цепь может состоять из нескольких функциональных блоков и образует замкнутую систему. Замкнутую систему называют одноконтурной, если при ее размыкании (отсоединении обратной связи от сумматора с y₀) получают цепочку из последовательно соединенных элементов. Замкнутые системы бывают и многоконтурными (рис. 2.5.4).Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала определить передаточные функции отдельных участков.

15-16) передаточная функция одноконтурной и многоконтурной схемы

Замкнутые системы бывают одноконтурными и многоконтурной (рис.32).Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала осуществить преобразование отдельных участков.

Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления эквивалентной передаточной функции нужны дополнительные правила:

4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено с передаточной функцией того звена, через которое переносится сумматор. Если сумматор переносится против хода сигнала, то добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим сумматор (рис.34).

Так с выхода системы на рис.34а снимается сигнал

y₂ = (f + y_oW₁)W₂.

Такой же сигнал должен сниматься с выходов систем на рис.34б:

y₂ = fW₂ + y_oW₁W₂ = (f + y_oW₁)W₂,

и на рис.34в:

y₂ = (f(1/W₁) + y_o)W₁W₂ = (f + y_oW₁)W₂.

При подобных преобразованиях могут возникать неэквивалентные участки линии связи (на рисунках они заштрихованы).

5. При переносе узла через звено по ходу сигнала добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим узел. Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией звена, через которое переносится узел (рис.35).

Так с выхода системы на рис.35а снимается сигнал

y₁ = y_oW₁.

Такой же сигнал снимается с выходов рис.35б:

y₁ = y_oW₁W₂/W₂ = y_oW₁

и рис.35в:

y₁ = y_oW₁.

6. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис. 36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор необходимо добавить сравнивающий элемент (рис.36в: y = y₁ + f₁ = > y₁ = y - f₁) или сумматор (рис.36г: y = y₁ + f₁).

Во всех случаях переноса элементов структурной схемы возникают неэквивалентные участки линии связи, поэтому надо быть осторожным в местах съема выходного сигнала.

При эквивалентных преобразованиях одной и той же структурной схемы могут быть получены различные передаточные функции системы по разным входам и выходам. Так на рис.48 имеется два входа: по управляющему воздействию u и возмущению f при одном выходе y. Такая схема может быть преобразована к одному звену с двумя передаточными функциями W_uy и W_fy.

17) Формула мейсона

Для многоконтурных схем, более сложных чем рассмотренная, процедуры предварительных переносов и последовательного свертывания оказываются достаточно трудоемкими. Поэтому для таких схем целесообразно использовать формулу Мейсона:

, (60)

где 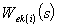– передаточная функция i-го прямого канала, связывающего вход с выходом ; m – число таких каналов; – специальный полином, который определенным образом характеризует совокупность всех замкнутых цепей системы, содержащих обратные связи, и вычисляется как сумма передаточных функций разомкнутых контуров этих цепей и произведений передаточных функций разомкнутых контуров пар, троек и т.д. не соприкасающихся друг с другом цепей с обратными связями: