При практических расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (логарифмические частотные характеристики – ЛЧХ). Они характеризуются большей линейностью и на определенных участках изменения частот могут быть заменены прямыми линиями и в целом представлены ломаными линиями. Причем отрезки прямых в большинстве случаев можно построить при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, т.к. умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.
За единицу длины по оси частот ЛЧХ принимается декада. Декада – интервал частот, заключенный между произвольным значением 
и его десятикратным значением. Отрезок, соответствующий одной декаде, равен 1.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
, дБ, (86)
ординаты которой измеряют в логарифмических единицах – белах или децибелах (0,1 бела), сокращенно дБ (рис. 23).
Бел – единица измерения отношения мощности двух сигналов. Если мощность одного сигнала больше мощности другого в 10 раз, то эти мощности отличаются на 1 Б (lg10 = 1).
Т.к. мощность сигнала пропорциональна квадрату амплитуды 
,то
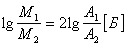
или
.
При построении фазовой частотной характеристики логарифмический масштаб применяется только для оси абсцисс.
Рис. 23. Логарифмическая амплитудно-частотная характеристика
Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.
Термин употребляется также в применении к передаточной функции системы, записанной в виде преобразования Фурье выходного сигнала, поделённого на преобразование Фурье входного сигнала.
20) Многоконтурные стационарные линейные системы
Пусть 
— входной сигнал линейной стационарной системы, а 
— её выходной сигнал. Тогда передаточная функция 
такой системы записывается в виде:
,
где 
и 
— преобразования Лапласа для сигналов и соответственно:
,
.
21) Нестационарные линейные системы
Определяющими свойствами для любой линейной стационарной системы являются линейность и стационарность:
- Линейность означает, что связь между входом и выходом системы удовлетворяет свойству. Формально, линейной называется система, обладающая следующим свойством: если сигнал на входе системы (воздействие) —
x (t) = A · x 1(t) + B · x 2(t)
тогда сигнал на выходе системы (реакция) —
y (t) = A · y 1(t) + B · y 2(t)
для любых постоянных A и B, где yi(t) — выход системы как реакция на входной сигнал (воздействие) x i(t).
- Стационарность — означает, что выходной сигнал системы как реакция на любой заданный входной сигнал одинаков для любого момента приложения входного сигнала (с точностью до времени запаздывания момента приложения входного сигнала). В более узком смысле — при запаздывании входного сигнала по времени на некоторую величину, выходной сигнал будет запаздывать на ту же самую величину.
Динамика систем, обладающих вышеперечисленными свойствами, может описываться одной простой функцией, к примеру, импульсной переходной функцией. Выход системы может рассчитываться как свёртка входного сигнала с импульсной переходной функцией системы. Этот метод анализа иногда называется анализом во временной области. Сказанное справедливо и для дискретных систем.
Связь между временно́й и частотной областями
Кроме того, любая ЛСС может быть описана в частотной области с помощью своей передаточной функции, которая является преобразование Лапласа импульсной передаточной функции (или Z-преобразованием в случае дискретных систем). В силу свойств этих преобразований, выход системы в частотной области будет равен произведению передаточной функции и соответствующего преобразования входного сигнала. Другими словами, свёртке во временной области соответствует умножение в частотной области.
Для всех ЛСС собственные функции являются комплексными экспонентами. То есть, если вход системы представляет собой комплексный сигнал 
с некоторой комплексной амплитудой 
и частотой 
, то выход будет равен некоторому сигналу 
с комплексной амплитудой 
. Отношение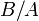 
будет являться передаточной функцией системы на частоте .
Так как синусоиды представляют собой сумму комплексных экспонент с комплексно-сопряжёнными частотами, если вход системы — синусоида, то выходом системы будет также синусоида, в общем случае с другой амплитудой и фазой, но с той же частотой.
Теория ЛСС хорошо подходит для описания многих систем. Большинство ЛСС гораздо проще анализировать, чем нестационарные и нелинейные системы. Любая система, динамика которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является линейной стационарной системой. Примерами таких систем являются электрические схемы, собранные из резисторов, конденсаторов и катушек индуктивности (RLC-цепочки). Груз на пружинке также можно считать ЛСС.
Большая часть общих концепций ЛСС схожа как в случае непрерывных систем, так и в случае дискретных систем.
22-23) Устойчивость линейных систем автоматического управления
Рассматривается уравнение
| x ′ = f (t, x), | (НС) |
| f: [ t 0, +∞) × R n → R n, | (2) |
| и фиксированное его решение x = φ(t) = gt 0 t (x 0) на [ t 0, +∞). Предполагается, что выполнены условия обобщенной теоремы Коши — Пикара. |
Решение φ называется
— устойчивым по Ляпунову, если (см. рис. 2а)
|
— асимптотически устойчивым, если (см. рис. 2б)
1) оно устойчиво,
| 2) ∃ (Δ > 0) ∀ (x 0: | x 0 – x 0| < Δ) [ gt 0 t (x 0)– gt 0 t (x 0)→ 0 при t → +∞]; |
— асимптотически устойчивым в целом, если оно асимптотически устойчиво, причем в 2) можно взять Δ = +∞; другими словами, 2) заменяется на
| 2') ∀ (x 0) [ gt 0 t (x 0)– gt 0 t (x 0)→ 0 при t →+∞]; |
— экспоненциально устойчивым, если
| ∃ (Δ1 > 0, M > 0, γ > 0) ∀(x 0: | x 0 – x 0| < Δ1) ∀ (t ≥ t 0) |
|
— экспоненциально устойчивым в целом, если в качестве Δ1 можно взять +∞, т. е.
|
Рис. 2.
Очевидно, экспоненциальная устойчивость решения влечет его асимптотическую устойчивость, которая, в свою очередь, влечет устойчивость. Нетрудно проверить также, что обратные импликации не справедливы (для второй это уже показано в п. 4.2.1).
| Как видно из определения, устойчивость решения φ(t) = gt 0 t (x 0)— это непрерывность семейства операторов сдвига { gt 0 t: t ≥ t 0} в точке x 0, равномерная относительно t ∈ [ t 0, +∞). Из теоремы об условии Липшица для оператора сдвига вытекает, что соответствующее семейство { gt 0 t: t ∈ [ t 0, t 1]} для любого отрезка [ t 0, t 1] в условиях обобщенной теоремы Коши — Пикара всегда равномерно непрерывно в любой точке x 0, т. к. |
|
В частности, так будет для уравнения (1) и при a > 0, хотя устойчивости нулевого решения нет.
| Пусть Φ t 0(t) — фундаментальная матрица (ЛОС), нормальная в t 0. Утверждается, что |
| (а) (ЛС) устойчива ⇔ Φ t 0(t) ограничена на [ t 0, +∞); |
| (б) (ЛС) асимптотически устойчива ⇔ Φ t 0(t) → 0 при t → +∞ ⇔ (ЛС) асимптотически устойчива в целом; |
| (в) (ЛС) экспоненциально устойчива ⇔ (M > 0, γ > 0) ∀ (t ≥ t 0) [||Φ t 0(t)|| ≤ Me –γ(t – t 0)] ⇔ (ЛС) экспоненциально устойчива в целом. |
Д о к а з а т е л ь с т в о. (а) Пусть (ЛС) устойчива, т. е. устойчиво нулевое решение (ЛОС). Положив в определении устойчивости ε = 1, найдем δ > 0 такое, что
| || x 0|| < δ ⇒ || gt 0 t (x 0)||= ||Φ t 0(t) x 0|| < 1 (t ≥ t 0). |
Следовательно, если || x || = 1, то ||δ x /2|| < δ и
|
| Поэтому ||Φ t 0(t)|| < 2/δ, т. е. Φ t 0(t) ограничена. |
Если, наоборот, известно, что
| ||Φ t 0(t)|| ≤ H (t ≥ t 0), |
то
| || gt 0 t (x 0)||≤ H || x 0||, |
так что для любого ε > 0 в определении устойчивости нулевого решения (ЛОС) можно взять δ = ε/ H.
(б) Пусть (ЛС) асимптотически устойчива. Тогда
| || x 0|| < Δ ⇒ ||Φ t 0(t) x 0|| → 0 при t → +∞. |
В частности для орта ek
|
| (мы рассматриваем произвольную норму в R n, поэтому, возможно, || ek || ≠ 1). Это означает, что все столбцы матрицы Φ t 0(t) стремятся к нулю при t → +∞; но тогда и сама матрица стремится к нулю. |
| Пусть дано, что Φ t 0(t) → 0 при t → +∞. Тогда для любого x 0 ∈ R n |
| gt 0 t (x 0)= Φ t 0(t) x 0 → 0 при t → +∞, |
т. е. (ЛС) асимптотически устойчива в целом.
Наконец, из асимптотической устойчивости в целом следует асимптотическая устойчивость.
(в) Если (ЛС) экспоненциально устойчива, то существуют Δ1 > 0, M > 0 и γ > 0 такие, что
| || x 0|| < Δ1 ⇒ ||Φ t 0(t) x 0|| ≤ Me –γ(t – t 0)|| x 0|| (t ≥ t 0). |
Поэтому для любого x, удовлетворяющего условию || x || = 1, будем иметь:
|
|
Следовательно,
| ||Φ t 0(t)|| ≤ Me –γ(t – t 0) (t ≥ t 0). |
Наоборот, если выполнено последнее неравенство, то для любого x 0
| ||Φ t 0(t) x 0|| ≤ ||Φ t 0(t)||·|| x 0|| ≤ Me –γ(t – t 0)|| x 0|| (t ≥ t 0), |
т. е. (ЛС) экспоненциально устойчива в целом.
Остается заметить, что экспоненциальная устойчивость в целом влечет экспоненциальную устойчивость.
24) Непрерывное и дискретное представление процессов управления
25) Программы дискретных управляемых устройств
26) Правила перехода от непрерывной передаточной функции к дискретной
27) Типы систем управления
Система автоматического управления, как правило, состоит из двух основных элементов — объекта управления и управляющего устройства.
По цели управления
Объект управления — изменение состояния объекта в соответствии с заданным законом управления. Такое изменение происходит в результате внешних факторов, например вследствие управляющих или возмущающих воздействий.