Закон Ома для переменного тока
Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:
U = I·Z

где:
· U = U0eiωt — напряжение или разность потенциалов,
· I — сила тока,
· Z = Re—iδ — комплексное сопротивление (импеданс),
· R = (Ra2+Rr2)1/2 — полное сопротивление,
· Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
· Rа — активное (омическое) сопротивление, не зависящее от частоты,
· δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой U = U0eiωt, что InU = U. Тогда все значения токов и напряжений в схеме надо считать как F = ImF.
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Чему равен сдвиг фаз между напряжением и током в цепи, содержащей катушку, ёмкость?
Сдвиг фаз — разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой. Сдвиг фаз является величиной безразмерной и может измеряться в градусах, радианах или долях периода. В электротехнике сдвиг фаз между напряжением и током определяет коэффициент мощности в цепяхпеременного тока.
В радиотехнике широко применяются RC-цепочки, сдвигающие фазу приблизительно на 60°. Чтобы сдвинуть фазу на 180° нужно включить последовательно три RC-цепочки. Применяется в RC-генераторах.
Наведённая во вторичных обмотках трансформатора ЭДС для любой формы тока совпадает по фазе и форме с ЭДС в первичной обмотке. При противофазном включении обмотоктрансформатор изменяет полярность мгновенного напряжения на противоположную, в случае синусоидального напряжения сдвигает фазу на 180°. Применяется в генераторе Мейснера и др.
 рис.305
рис.305
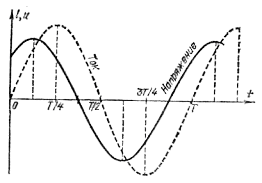
Рис. 305. Опыт по обнаружению сдвига фаз между током и напряжением: слева — схема опыта, справа — результаты
дает форму напряжения между обкладками конденсатора (точками а и b), потому что в этой петле осциллографа ток в каждый момент времени пропорционален напряжению. Опыт показывает, что в этом случае кривые тока и напряжения смещены по фазе, причем ток опережает по фазе напряжение на четверть периода (на p/2). Если бы мы заменили конденсатор катушкой с большой индуктивностью (рис. 305, б), то оказалось бы, что ток отстает по фазе от напряжения на четверть периода (на p/2). Наконец, таким же образом можно было бы показать, что в случае активного сопротивления напряжение и ток совпадают по фазе (рис. 305, в).
В общем случае, когда участок цепи содержит не только активное, но и реактивное (емкостное, индуктивное или и то и другое) сопротивление, напряжение между концами этого участка сдвинуто по фазе относительно тока, причем сдвиг фаз лежит в пределах от +p/2 до —p/2 и определяется соотношением между активным и реактивным сопротивлениями данного участка цепи.
В чем заключается физическая причина наблюдаемого сдвига фаз между током и напряжением?
Если в цепь не входят конденсаторы и катушки, т. е. емкостным и индуктивным сопротивлениями цепи можно пренебречь по сравнению с активным, то ток следует за напряжением, проходя одновременно с ним через максимумы и нулевые значения, как это показано на рис. 305, в.
Если цепь имеет заметную индуктивность L, то при прохождении по ней переменного тока в цепи возникает ЭДС. самоиндукции. Эта ЭДС по правилу Ленца направлена так, что она стремится препятствовать тем изменениям магнитного поля (а следовательно, и изменениям тока, создающего это поле), которые вызывают э. д. с. индукции. При нарастании тока э. д. с. самоиндукции препятствует этому нарастанию, и потому ток позже достигает максимума, чем в отсутствие самоиндукции. При убывании тока э. д. с. самоиндукции стремится поддерживать ток и нулевые значения тока будут достигнуты в более поздний момент, чем в отсутствие самоиндукции. Таким образом, при наличии индуктивности ток отстает по фазе оттока в отсутствие индуктивности, а следовательно, отстает по фазе от своего напряжения.
Если активным сопротивлением цепи R можно пренебречь по сравнению с ее индуктивным сопротивлением XL=wL, то отставание тока от напряжения по времени

равно Т/4 (сдвиг фаз равен p/2), т. е. максимум u совпадает с i=0, как это показано на рис. 305, б. Действительно, в этом случае напряжение на активном сопротивлении Ri=0, ибо R=0, и, следовательно, все внешнее напряжение u уравновешивается ЭДС индукции, которая противоположна ему по направлению: u=LDi/Dt. Таким образом, максимум u совпадает с максимумом Di/Dt, т. е. наступает в тот момент, когда i изменяется быстрее всего, а это бывает, когда i=0. Наоборот, в момент, когда i проходит через максимальное значение, изменение тока наименьшее (Di/Dt=0), т. е. в этот момент u=0.
Если активное сопротивление цепи R не настолько мало, чтобы им можно было пренебречь, то часть внешнего напряжения и падает на сопротивлении R, а остальная часть уравновешивается э. д. с. самоиндукции: u=Ri+LDi/Dt. В этом случае максимум i отстоит от максимума и по времени меньше, чем на T/4 (сдвиг фаз меньше p/2), как это изображено