Лабораторная работа № 4
«Производственная логистика»
Планирование загрузки производственных мощностей
Пример. План выгодного производства
Цех компании может выпускать два вида продукции: рекламные стойки с центральной опорой и стойки двухсторонние.
На каждую стойку с центральной опорой расходуется 3,5 м пластика, 1 м металлической трубки и 1 человеко-день трудозатрат. Стойку двухстороннюю – 1 м пластика, 2 м металлической трубки и 1 человеко-день трудозатрат.
Прибыль от продажи 1 стойки с центральной опорой составляет 200 у.е., а 1 двухсторонней -100 у.е.
Материальные и трудовые ресурсы ограничены: в цехе работают 150 рабочих, в день нельзя израсходовать больше 350 м пластика и более 240 м металлической трубки.
Какое количество рекламных стоек с центральной опорой и двухсторонних должен выпускать цех, чтобы сделать прибыль максимальной?
Прежде всего сведем данные – параметры, характеризующие работу цеха, – в следующую таблицу (табл. 1).
Таблица 1. Параметры задачи
| Ресурсы | Запасы | Продукты | |
| Стойка с центральной опорой | Стойка двухсторонняя | ||
| Пластик | 3,5 | ||
| Металлическая трубка | |||
| Труд | |||
| Прибыль |
В колонке "Запасы" запишем предельный расход ресурсов (Пластика, металла и количества человеко-дней), которые ежедневно может позволить себе начальник цеха.
В колонках " Стойка с центральной опорой " и " Стойка двухсторонняя " (продукты, которые может выпускать цех) запишем расход имеющихся ресурсов на единицу продукции (т.е. сколько требуется Пластика, металла и труда на одну стойку того и другого типа).
Наконец, на пересечении колонок " Стойка с центральной опорой " и " Стойка двухсторонняя " и строки "Прибыль" запишем величины прибыли от продажи одной единицы каждого продукта.
Определим теперь все элементы математической модели данной ситуации (табл. 2):
- переменные решения,
- целевую функцию и
- ограничения.
Таблица 2. Элементы модели
| Переменные решения | Целевая функция |
| X1 – количество стоек с центральной опорой X2 – количество Стоек двухсторонних, производимых ежедневно | Р = 200 × X1 + 100 × X2 Ежедневная прибыль цеха |
| Ограничения | |
| 3,5 × Х1 + 1 × Х2 £ 350 1 × Х1 + 2 × Х2 £ 240 1 × Х1 + 1 × Х2 £ 150 Х1, Х2 ³ 0 |
В данном случае очевидно, что переменные решения (иначе - неизвестные), которые может задавать начальник цеха и от которых зависит целевая функция (прибыль) цеха, – это количество стоек с центральной опорой и двухсторонних, выпускаемых цехом ежедневно.
Обозначим эти переменные соответственно X1, и Х2.
Нетрудно также понять, как в данном случае записывается выражение для целевой функции. Прибыль от продажи одной стойки с центральной опорой равна 200 у. е., значит, прибыль от продажи X1, стоек с центральной опорой будет 200× Х1. Аналогично прибыль от продажи X2 стоек двухсторонних равна 100 × Х2, что и отражено в соответствующей графе таблицы.
Глядя на выражение для целевой функции (типичное для моделей линейного программирования), можно легко увидеть, что, чем больше будут значения переменных X1 и Х2, тем больше будет и прибыль Р. Если бы было возможно беспредельно увеличивать ежедневный выпуск стоек обоих типов, прибыль росла бы беспредельно. Ясно, однако, что это невозможно, поскольку доступные ежедневно ресурсы цеха ограниченны. Это приводит к ограничениям на значения переменных X1 и Х2.
Теперь ограничения. Проще начать с ограничения, которое вытекает из ограниченности трудовых ресурсов. Поскольку каждый рабочий за 1 день может сделать либо 1 стойку с центральной опорой, либо 1 двухстороннюю, ясно, что общее количество выпущенных изделий не должно превышать числа рабочих в Цехе. Иначе можно сказать, что поскольку расход трудового ресурса равен 1 человеко-дню на 1 стойку с центральной опорой и 1 человеко-дню на 1 двухстороннюю, то общий расход труда на Х1 стоек и Х2 стоек будет, очевидно,
1 × Х1 + 1 × Х2,
что не должно превышать ежедневного "запаса труда" в цехе, т.е. 150 человеко-дней. Это отражено последним неравенством, написанным в таблице элементов модели.
Аналогично записывается неравенство, отражающее ограниченность ежедневных запасов пластика. Поскольку на 1 стойку с центральной опорой расходуется 3,5 м пластика, а на 1 двухстороннюю стойку – 1 м, то суммарный расход пластика на Х1 стоек и Х2 стоек будет, очевидно,
3,5 × Х1 +1 × Х 2,
что не должно превышать ежедневного запаса пластика в цехе, т.е. 350 м. Это отражено первым неравенством, записанным в табл. 2.
Точно так же получается и второе неравенство, отражающее ограниченность ежедневных запасов металлической трубки.
Определение переменных решения, целевой функции и ограничений – это почти все, что должен сделать менеджер, чтобы воспользоваться результатами оптимизации и анализа линейной модели. Далее необходимо только правильно организовать данные для компьютера, а все остальное сделает компьютерный алгоритм оптимизации.
Решение задачи об оптимальной производственной программе с помощью Excel
1. Организуйте данные на листе MS-Excel так, как это показано на рис. 1.
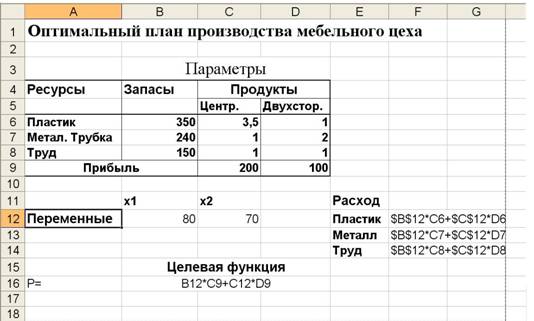 |
Рис. 1. Организация данных на листе MS-Excel для примера " Оптимальный план выпуска продукции "
a) В ячейку В16 введена целевая функция Р = 200 × Х1 + 100 × Х2, представляющая собой прибыль от продажи Х1 стоек и Х2 стоек.
b) В ячейки F12, F13, F14- формулы, отражающие расход ресурсов при изготовлении Х1 стоек и Х2 стоек:
| Пластик | 3,5 × Х1 + 1 × Х2 |
| Металлическая трубка | 1 × Х1 + 2 × Х2 |
| Труд | 1 × Х1 + 1 × Х2 |
2. Выберите пункт меню "Сервис" "Поиск решения". Появится окно, озаглавленное "Поиск решения" – рис. 2.
 |
Рис. 2. Общий вид и работа с окном "Поиск решения"
а) В поле окна "Установить целевую ячейку" отметьте ячейку В16 (щелкните сначала по полю окна, а затем по ячейке В16);
b) Установите переключатель на отметке "Равной максимальному значению";
c) В поле окна "Изменяя ячейки" отметьте ячейки В12:С12 (аналогично пункту а).
Добавьте ограничения, щелкая по кнопке "Добавить".
В появившемся окне, озаглавленном "Добавление ограничения" (рис. 3), щелкните по полю "Ссылка на ячейку", а затем отметьте ячейки В12:С12, выберите знак ограничения, щелкните по правому полю "Ограничение" (Constraints) и введите в него значение 0. Таким образом, вы ввели ограничение Х1,Х2 < 0. Вновь щелкните по кнопке "Добавить".

Рис. 3. Общий вид и работа с окном "Добавление ограничения"
e) В появившемся окне "Добавление ограничения" щелкните в поле "Ссылка на ячейку", а затем отметьте ячейку F12, выберите знак ограничения (, щелкните по правому полю "Ограничение" (Constraints) и отметьте в нем ячейку В6, содержащую ограничение на ресурс "ДСП". Таким образом, вы ввели ограничение 3,5 × Х1 + Х2 £ 350;
f) Продолжайте процесс, пока не введете остальные два ограничения.
3. Щелкните по кнопке "Параметры" (Options).
Появится окно "Параметры поиска решения" (рис. 4), в котором можно (но не нужно) менять многочисленные параметры оптимизации. Вас интересует только, установлен ли флажок "Линейная модель". Если нет, установите его, щелкните по кнопке Ok и вернитесь к окну "Поиск решения".

Рис. 4. "Параметры поиска решения" в MS-Excel
Установка параметров оптимизации в окне "Поиск решения" должна выглядеть так, как показано на рис. 5.
 |
Рис. 5. Ввод данных для примера "Оптимальный план выпуска продукции мебельного цеха" в окно "Поиск решения"
4. Щелкните по кнопке "Выполнить".
Оптимизационная программа MS-Excel выполнит поиск решения, после чего появится окно "Результаты поиска решения" (рис. 6). Прочтите сообщение программы в этом окне. Если вы все сделали правильно, программа сообщит: "Решение найдено. Все ограничения и условия оптимальности выполнены".
 |
Рис. 6. Вид окна "Результаты поиска решения"
Вид листа MS-Excel, соответствующий оптимальному решению, показан на рис. 7.
 |
Рис.7. Результаты решения примера " Оптимальный план выпуска продукции компании " на листе MS-Excel
5. В этом случае убедитесь, что переключатель в окне "Результаты поиска решения" находится в положении "Сохранить найденное решение", щелкните по кнопке Ok и прочтите ответ в ячейках В12:С12.
В ячейках F12:F14 содержатся значения ресурсов, которые необходимы для полученного оптимального плана.
В случае, если вы неверно задали знак ограничений, ввели неверные формулы для целевой функции или для ограничений и оптимизационная программа не может найти решения, в окне появятся сообщения:
"Значения целевой ячейки не сходятся" или:
"Поиск не может найти решения", или:
"Условия линейной модели не выполняются".
В этом случае следует переставить переключатель в окне "Результаты поиска решения" в положение "Восстановить исходные данные", щелкнуть по кнопке Ok и проверить организацию данных на листе Excel и в установках окна "Поиск решения".
Пример. План организации обеспечения строительными материалами
В области имеются два завода и три потребителя их продукции - домостроительные комбинаты. В таблице указаны суточные объемы производства цемента, суточные потребности в нем комбинатов и стоимость перевозки 1т цемента от каждого завода к каждому комбинату.
| Заводы | Производство цемента (т/сут,) | Стоимость перевозки 1т цемента, руб. | ||
| Комбинат 1 | Комбинат 2 | Комбинат 3 | ||
| Потребности в цементе |
Требуется составить план суточных перевозок цемента с целью минимизации транспортных расходов.
Решение В качестве неизвестных величин выступают объемы перевозок. Пусть xij- объем перевозки цемента с i- го завода на j- й комбинат, Pij - стоимость перевозки 1т цемента с i- гозавода на j- й комбинат. Тогда функция цели представляет собой суммарные транспортные расходы:
 - Эту функцию надо минимизировать.
- Эту функцию надо минимизировать.
Неизвестные в данной задаче должны удовлетворять следующим ограничениям:
· Объемы перевозок не могут быть отрицательными, т.е. xij ≥ 0.
· Весь цемент с заводов должен быть вывезен. Пусть аi - объем производства цемента на i -ом заводе. Тогда это ограничение выглядит следующим образом: 
· Потребности всех комбинатов в цементе должны быть удовлетворены. Если за bj обозначить потребность в цементе j -го комбината, то это условие может быть записано так: 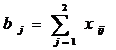
Исходные данные можно расположить на рабочем листе, как показано на рис. 7. При подготовке примера были сделаны такие установки, чтобы в ячейках рабочего листа отображались формулы, а не значения, вычисляемые с помощью этих функций, что показать какие формулы нужно использовать для реализации функции цели и ограничений. Для решения задачи отображать формулы вместо значений не нужно. После подготовки рабочего листа нужно вызвать Поиск решения и заполнить диалоговое окно, как показано на рис. 8. Кроме того, нужно воспользоваться кнопкой Параметры и затем установить флажок Линейная модель.

Рис. 7. Исходные данные для задачи о перевозке цемента

Рис 8. Задание исходныхданных для окна Поиска решения
После нажатия кнопки Выполнить средство Поиск решения найдет оптимальный план суточных перевозок цемента.
Замечание. В рассмотренном примере задача является сбалансированной: суммарный объем произведенной продукции равен суммарному объему потребности в ней. Поэтому в этой модели не надо учитывать издержки, связанные со складированием (при перепроизводстве) или с недопоставками (при дефиците). В противном случае в модель нужно было бы ввести:
- в случае перепроизводства - фиктивный комбинат, стоимость перевозок единицы продукции в который будет равна стоимости складирования, а потребности в продукции - объемам складирования излишков продукции на заводах;
- в случае дефицита - фиктивный завод, стоимость перевозок с которого будет равна стоимости штрафов за недопоставку продукции, а объемы перевозок - объемам недопоставок продукции в пункты распределения.
Задача Планирование загрузки производственных мощностей (для самостоятельного решения)
Фирма «Мастер-Шина» имеет 10 филиалов в разных городах страны, которые могут производить 6 видов продукции. Необходимые для решения известные данные (фонд рабочего времени, величина потребности в продукции, мощность, себестоимость продукции) по каждому виду (или предприятию) дана в таблице 1.
Таблица 1 – Условия задачи.
| Продукция | Фонд рабочего времени | |||||||
| Предприятия | ||||||||
| Потребность | 1 000 | 1 500 | 2 500 | 1 300 | 1 400 |
Таблица 2 – Условия себестоимости продукции.
| Продукция | |||||||
| Предприятия | 2 362 | 1 756 | 2 483 | ||||
| 1 263 | 1 865 | 1 249 | 1 756 | 2 368 | |||
| 2 502 | 1 749 | 1 751 | 2 867 | ||||
| 1 245 | 1 249 | 1 741 | |||||
| 1 627 | 2 128 | 2 616 | 1 132 | 1 382 | |||
| 1 864 | 2 132 | 1 995 | |||||
| 1 503 | 2 244 | 2 243 | 2 737 | 1 119 | |||
| 1 118 | 1 501 | 2 980 | 1 872 | 1 626 | |||
| 2 003 | 2 620 | 1 261 | 1 880 | ||||
| 1 262 | 1 509 | 2 872 | 2 110 |
Перед руководством фирма поставлена задача нахождения такого оптимального распределения производственных мощностей, при котором суммарные затраты по изготовлению продукции в заданной номенклатуре будут минимальными при полной загрузке производственных мощностей предприятий.
Пусть xij – планируемый объём выпуска j -ой продукции на i -м предприятии; совокупность таких величин обозначим 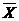 . Тогда целевая функция рассматриваемой задачи имеет вид
. Тогда целевая функция рассматриваемой задачи имеет вид
 (1)
(1)
при ограничениях
 (2)
(2)
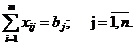 (3)
(3)
 (4)
(4)
где
m – число предприятий (филиалов);
n – количество видов продукции;
ai – фонд рабочего времени (например, в сменах) каждого i- го предприятия; i= 1, 2, …, m;
bii – величина потребности в продукции j -го вида, j=1,2,…,n;
aij – мощность, или количество продукции j- го вида, вырабатываемой (в смену) на i- ом предприятии;
cij – себестоимость производства единицы j- ой продукции на i- ом предприятии.
Если снять условия полной загрузки производственных мощностей (в некоторых случаях при этом условии модель может не сходиться, следовательно, правильного оптимального решения достигнуть не удастся), то ограничения (2) примут вид неравенства:

Если условие точного выполнения плана в заданной номенклатуре заменить требованием «не меньше», то условия (3) в свою очередь превратятся в неравенство:

При заданной математической модели поиск решения задачи не составит труда при использовании средства Microsoft Excel для создания необходимой компьютерной модели ситуации.
 Для начала необходимо сформировать таблицу с данными условиями в книге Microsoft Excel.
Для начала необходимо сформировать таблицу с данными условиями в книге Microsoft Excel.
Затем необходимо составить рабочую область решения – таблицу «ЗАКАЗЫ», в которой будут находиться ячейки для поиска решения, а также столбец «Загрузка мощностей» (формула 2) и строка «Производство товара», которая будет содержать суммарные заказы на всех филиалах по каждому виду продукции. Ячейка «Суммарные затраты» содержит в себе формулу (1). Она и будет являться целевой функцией.

Подсказка: для удобства и простоты создания формулы для целевой функции необходима вспомогательная строка 42, в ячейках которой содержатся формулы суммы произведений заказов на продукцию по каждому филиалу на соответствующую себестоимость этой продукции для филиала Тогда формула ячейки суммарных затрат будет содержать лишь только сумму ячеек вспомогательной строки. Для удобства и наглядности работы цвет шрифта строки 42 выбран «Белым», чтобы не загромождать внешний вид модели.
Теперь остаётся только занести необходимые ограничения в надстройку «Поиск решения» (заказы на продукцию должны быть неотрицательны, нельзя производить товара больше, чем он затребован у населения, нужно также установить необходимый минимум производства, т.е. минимум 1000 (значение ячеек в строке «Производство» должно быть не меньше 1000), также необходимо установить условие полной загрузки производственных мощностей по формуле 2).
Нажимаем на кнопку «Выполнить» и через несколько секунд компьютер выдаёт правильное оптимальное решение. Для удобства работы с результатами оптимизации можно создать альтернативную таблицу ответов, в ячейках которых будет содержаться функция условия (оформляется через функцию «ЕСЛИ» Microsoft Excel), которая будет отображать значение соответствующей ячейки таблицы ответов, либо отображать знак “–”, если таблица ответов будет содержать «0».

Из рисунка видно, что минимальные суммарные затраты распределения составили 19307478 д.е. Причём продукция второго вида не получила заказов, соответственно производить её оказывается неэффективно. В данном случае можно установить при необходимости условие необходимого минимума на производство данного вида продукции, но это уже будет решать руководство предприятия.
Подсказка: условие можно установить просто введя дополнительное ограничение: ячейка «Производство товара» по данному виду продукции должна быть не меньше какой-либо установленной величины. Например 1000.
Таким образом на основании приведённой модели руководство предприятия может установить необходимое оптимальное распределение загрузки производственных мощностей по всем своим филиалам при условии минимизации суммарных затрат на выпуск продукции.
Задача Планирование загрузки производственных мощностей (для самостоятельного решения)
Завод изготовляеткорпуса для холодильников икомплектует ихоборудованием, поставляемым без ограничений другимипредприятиями. В таблице указанынормы трудозатрат, затрат материалов для изготовлениякорпусов, ограничения по этимресурсам в расчете на месяц иприбыль от реализациихолодильника каждой из пяти марок. Найти месячный план выпускахолодильников, максимизирующийприбыль.
| Наименование ресурса | Марка холодильника | Объем ресурса | ||||
| Трудозатраты (чел./ч.) | ||||||
| Металл (м2) | ||||||
| Пластик(м2) | ||||||
| Краска (кг) | ||||||
| Прибыль (р.) |
Задача Планирование загрузки производственных мощностей (для самостоятельного решения)
Нефтеперерабатывающий завод производит за месяц 1500000 лалкилата,1200000 л крекинг-бензинаи 1300000 л изопентана. В результате смешивания этих компонентов в пропорциях 1:1:1и 3:1:2 получается бензин сорта А и Б соответственно.Стоимость 1000л бензинасорта А иБ соответственно равна 90 р. и120 р.
Определить месячный план производства бензинасорта А и Б, максимизирующий стоимость выпускаемой продукции.
Планирование материальных потребностей (MRPI).
Пример Планирование материальных потребностей
Когда мы имеем дело непосредственно с производственным процессом, то спрос по своей форме (как рыночный спрос на конкретные изделия) из независимого превращается в зависимый, поскольку каждое изделие состоит из конкретных составных частей, входящих в состав изделия. Спрос на эти составные элементы будет зависимым от количества изделий, удовлетворяющих рыночную потребность, т. е. от количества выпускаемых конкретных изделий. К таким зависимым элементам относятся материалы, детали и узлы, т. е. все компоненты, входящие в конкретные изделия, представляют компоненты зависимого спроса. Когда связи между зависимыми элементами определены, можно для любого компонента любого наименования составить план, выраженный в количествах вхождения этого компонента в конечное изделие, и определить расписание производства или потребления компонент в соответствии с конечным сроком производства изделия. С этой целью используются методы зависимого спроса на материалы, детали и узлы, которые рекомендуется использовать в рамках мелкосерийного, единичного и серийного типов производства. Эти методы носят название ПЛАНИРОВАНИЕ ПОТРЕБНОСТИ В МАТЕРИАЛАХ (MRP). Когда методы зависимого спроса используются в распределительной сфере, они называются ПЛАНИРОВАНИЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ (DRP).
Необходимо рассмотреть задачи с использованием модели потребности зависимых запасов для случаев производства и распределения. Чтобы пользоваться такими моделями, необходимо знать:
1) производственный график (что должно быть и когда);
2) спецификации или ведомости применяемых материалов (из чего состоит изделие);
3) наличие материалов на складе (в заделе); что на складе;
4) материалы в заявке (что заказано);
5) время изготовления (как много требуется времени, чтобы получить компонент).
Исходные данные для решения задачи MRPI приведены в табл. 2.7,2.8 и 2.10.
Изделие А состоит из сборочных единиц В и С, В включает D и С, а С — E и F. Количество составных элементов для изготовления компоненты или изделия более высокого уровня для сборочных единиц и деталей проставлены в скобках.
Таблица 2.7 Производственное расписание на изготовление изделия А
| Изделие | Недели планового периода | |||||||
| …. | ||||||||
| А | … |
Таблица 2.8 Структура изделия А
| A | ||||
| B(1) | C(1) | |||
| D(2) | C(2) | |||
| E(1) | F(1) | E(1) | F(1) | |
Расчет количества составных элементов для сборки изделия А в количестве 50 шт. для 8-й и 11-й недели, и 100 шт. для 13-й недели сводится в табл. 2.9.
Таблица 2.9 Расчет полной потребности в составных элементах (без учета наличного запаса) для изготовления партии изделия А
| Элемент | Количество | |
| А | 50 шт. (для 8-й и 11-й недели) | 100 шт. (для 13-й недели) |
| В(1) | 1х 50 = 50 | 1 х 100 = 100 |
| D(2) | 1х 2 х 50= 100 | 1 х 2 х 100 = 200 |
| С(2) | 1 x 2 x 50= 100 | 1 x 2 x 100 = 200 |
| Е(1) | 1 x 2 x 1 x 50= 100 | 1 x 2 x l х 1 х 100 = 200 |
| F(l) | 1 х 2 х 1х 50= 100 | 1 x 2 x 1 x 100 = 200 |
| С(1) | 1 х 50 = 50 | 1 x 100= 100 |
| Е(1) | 1 x l х50 = 50 | 1 x 1 х 100= 100 |
| F(l) | 1 х 1 х 50 = 50 | 1 x l х 100= 100 |
Время изготовления или сборки ti (время опережения) для каждого элемента, а также наличный запас zni представлены в табл. 2.10.
Таблица 2.10 Время обработки и наличный запас для каждого элемента
| Элемент | Время обработки ti(недели) | Наличный запас zni. (шт.) |
| А | ||
| В | ||
| С | ||
| D | ||
| Е | ||
| F |
Совокупные расчеты по календарному планированию сводятся в табл. 2.11.

Варианты для самостоятельной работы студентов



