Изобразить векторную диаграмму для цепи, содержащей R, C и L.

§ напряжение.

Векторная диаграмма для RLC-цепочки. (Стрелки в нижней части рисунка не являются векторами векторной диаграммы, а лишь показывают участки цепи, напряжения на которых соответствует векторам с таким же буквенным обозначением и цветом в верхней части рисунка, как раз и являющейся собственно векторной диаграммой).

Последний вариант построения векторной диаграммы (для последовательно соединенных резистора, индуктивности и конденсатора) приведен на рисунке.

Подробно

В последовательную цепь (как на рисунке) включены резистор сопротивлением R, конденсатор емкостью C и катушка индуктивностью L. Обозначим напряжение на каждом из этих элементов соответственно U_R,U_C,U_L, а ток через цепь (одинаковый для каждого элемента из-за их последовательного включения) обозначим I.

Напряжение на концах цепи (которое мы обозначим как U_RLC) будет суммой напряжений на каждом элементе:

Полагаем (по условию задачи^[11]), что ток в цепи синусоидальный, и изображаем его на векторной диаграмме (верхняя часть рисунка) как горизонтальный вектор длиной, равной амплитуде тока (это означает, что мы принимаем начальную фазу тока за ноль; если она не ноль в реальном случае, то такой случай сводится к нашему сдвигом начала отсчета времени или поворотом всей векторной диаграммы целиком на угол начальной фазы, что ничего не меняет в последующих рассуждениях).

Полагаем (также по условию задачи), что частота тока (а следовательно и напряжений) задана и равна ω.

Напряжение на каждом из элементов цепи вычисляется исходя из его активного или реактивного сопротивления, а именно амплитуды напряжений, соответствующие длинам векторов, которыми эти напряжения изображаются на диаграмме, равны:

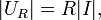
причем первое не сдвинуто по фазе относительно тока, а значит изображается на диаграмме вектором, сонаправленным с I, второе - в силу^[12] емкостного характера его реактивного сопротивления - отстает по фазе на 90°, а значит изображается вектором, повернутым на 90° в отрицательном направлении (по часовой стрелке) - то есть на рисунке вниз (поскольку I на этом рисунке строго горизонтально), а третье - силу^[13] индуктивного характера его реактивного сопротивления - обгоняет ток по фазе на 90°, а значит на диаграмме изображается вектором, повернутым на 90° в положительном направлении (против часовой стрелки) - на нашем рисунке это получается строго вверх.

Далее складываем U_R,U_C,U_L по правилам сложения векторов, то есть, как на рисунке, строим цепочку векторов (ломаную), где каждый следующий прибавляемый вектор строится так, чтобы его начало совпадало с концом предыдущего.

Вектором суммы оказывается, как мы и полагали выше

однако теперь мы видим этот вектор на диаграмме конкретно.

Длина этого вектора оказывается длиной гипотенузы прямоугольного треугольника со сторонами | U_R | и || U_L |-| U_C || (на рисунке изображен случай, когда | U_L | > | U_C |, однако это никак не скажется на последующих вычислениях).

Следовательно, по теореме Пифагора,

а подставляя длины векторов U_R, U_L, U_C из формул, выписанных выше, имеем

где I₀ обозначена амплитуда тока (равная длине вектора I); вынося I₀ из-под корня, имеем:

то есть аналитическое выражение для амплитуды напряжения на цепи.

По тем же соображениям (рассмотрение треугольника), находим угол, на который повернут вектор U_RLC относительно вектора I: