ЛАБОРАТОРНАЯ РАБОТА №
ИССЛЕДОВАНИЕ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА.
Цель проведения работы.
Целью проведения лабораторной работы является проверка закона Ома для неразветвленной цепи однофазного переменного тока состоящего из активного, индуктивного и емкостного сопротивлений.
Задачи проведения лабораторной работы.
В результате проведения лабораторной работы студенты должны:
· знать закона Ома и основные свойства неразветвленной цепи однофазного переменного тока состоящего из активного, индуктивного и емкостного сопротивлений;
· уметь собирать простейшие электрические схемы, выбирать электроизмерительные приборы, измерять основные электрические величины, проводить вычисления и делать выводы.
Перечень наглядных пособий, оборудования и электроизмерительных приборов.
При выполнении этой лабораторной работы используются: источник переменного трехфазного тока с напряжением 220 В (2), проволочный резистор (24), катушка индуктивности (25), конденсатор (26), амперметр (9, 15) и вольтметр (18) электромагнитной системы, ваттметр электродинамической системы, соединительные провода.
Теоретический материал.
Электрическая цепь с последовательным соединением активных, индуктивных и емкостных элементов называется последовательным колебательным контуром.
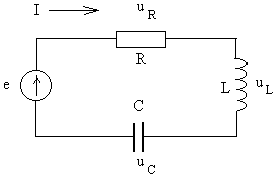
Будем считать, что под действием Э.Д.С. источника электрической энергии в рассматриваемой цепи протекает синусоидальный ток:
i = im sin wt.
Напряжение на активном сопротивлении:
uR = uRm sin wt.
Напряжение на катушке индуктивности:
uL = uLm sin (wt + p/2).
Напряжение на конденсаторе:
uC = uCm sin (wt - p/2).
Падение напряжения на всех элементах рассматриваемого контура определяется как сумма напряжений на всех элементах:
u = uR + uL + uC
Построим векторную диаграмму при условии, что XL < XC, то естьUL < UC..Векторная диаграмма строится для действующих значений:
UR=IR, UL=IXL,, UC=IXC
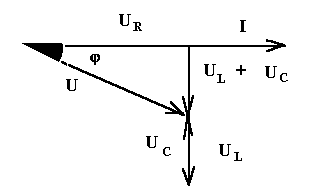
Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL, UC. Вектор (UL + UC) определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на индуктивности и емкости. Это объясняется процессом обмена энергией между индуктивностью и емкостью.
Получим закон Ома для рассматриваемой цепи. Модуль вектора (UL + UC) рассчитывается как разность действующих значений (UL - UC). Из векторной диаграммы следует, что
U = (UR2 + (UL - UC)2 )1/2.
Но UR = IR, а UС = IXС и UL = IXL, следовательно
U = I (R2 + (XL - XC)2)1/2,
откуда
I = U / (R2 + (XL - XС)2)1/2.
Введем обозначение (R2 + (XL - XС)2)1/2 = Z, где Z - полное сопротивление цепи. Закон Ома для этой цепи:
I = U / Z.
Разность между индуктивным и емкостным сопротивлением (XL - XС) называют реактивным сопротивлением цепи.
Прямоугольный треугольник образованный векторами напряжений UR, (UL + UC), U называется треугольником напряжений. Поскольку все элементы в рассматриваемой цепи соединены последовательно, то через все элементы цепи протекает один и тот же ток, то уравнение, связывающее напряжения U = (UR2 + (UL - UC)2 )1/2 , переходит в уравнение:
Z2 = [ R2 + (XL - XС)2 ]2.
Этому уравнению можно сопоставить прямоугольный треугольник, называемый треугольником сопротивлений:
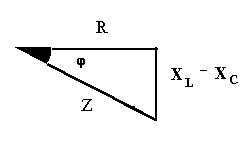
При XL > XС реактивное сопротивление положительно и сопротивление носит активно-индуктивный характер. При XL < XС реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостной характер. Знак сдвига фаз между током и напряжением получим автоматически, так как реактивное сопротивление - величина алгебраическая:
tg j = X / R.
Таким образом, при XL ¹ XС преобладает или индуктивное или емкостное сопротивление, то есть с энергетической точки зрения цепь с R, LиC сводится к цепи с R, LилиR, C.
Мгновенная мощность:
p = ui = UI cos j - UI cos (2wt + j).
Знак j определяется из tg j = X / R. Активная, реактивная и полная мощность такой цепи определяется равенствами:
P = UI cos j, Q = U I sin j, S = UI = (P2 + Q2)1/2.
Треугольник мощности для этой цепи имеет вид:
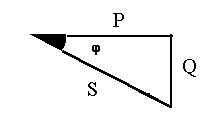
На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой активно-индуктивную нагрузку в виде асинхронных электродвигателей, силовых трансформаторов, сварочных трансформаторов, преобразователей и так далее. В такой нагрузке в результате протекания переменного тока индуктируются э.д.с. самоиндукции, обуславливающие сдвиг по фазе между током и напряжением. Этот сдвиг по фазе обычно увеличивается, а cos jуменьшается при малой нагрузке. Например, если cos jдвигателей переменного тока при полной нагрузке составляет 0,75 - 0,8, то при малой нагрузке он уменьшается до 0,2 - 0,4.
Если мощность потребляемая всеми приемниками в данных цепях, является вполне определенной, то при неизменном напряжении на зажимах приемника их ток:
I = P / (U×cosj)
С уменьшением cos jток нагрузки электростанций и подстанций будет увеличиваться при одной и той же отдаваемой мощности.
Вместе с тем электрические генераторы, трансформаторы и линии электропередач рассчитываются на определенное напряжение и ток. Увеличение тока потребителя при снижении cos j не должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощность Sном = Uном ×Iном, вследствие чего они не должны оказаться перегруженными. Для того чтобы ток генератора не превышал номинального значения при снижении cos j потребителя, необходимо снижать его активную мощность. Таким образом, понижение cos j потребителей вызывает неполное использование мощности синхронных генераторов, трансформаторов и линий электропередач. Они бесполезно загружаются за счет индуктивного реактивного тока
Величину cos j, характеризующую использование активной мощности, часто называют коэффициентом мощности.
Коэффициентом мощности называют отношение активной мощности к полной:
cos j = P/S
Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Нормальным считается cos j » 0,85 - 0,9. При низком коэффициенте мощности на предприятия, потребляющие электроэнергию, накладывается штраф, при высоком - предприятия премируются.
Для улучшения коэффициента мощности проводится ряд мероприятий:
· заменяются двигатели переменного тока, нагруженные относительно мало, двигателями меньшей мощности;
· включаются параллельно приемникам конденсаторы.
В электротехнике под резонансным режимом работы цепей переменного тока понимают режим, при котором сопротивление цепи является чисто активным. По отношению к источнику питания элементы цепи ведут себя в резонансном режиме как активное сопротивление, поэтому ток и напряжение в неразветвленной части цепи совпадают по фазе. Реактивная мощность цепи при этом равна нулю.
Возможны два основных случая резонанса: при последовательном соединении реактивных элементов контура с источником возможен резонанс напряжений, а при параллельном соединении - резонанс токов.
Резонансом напряжений называют явление в цепи с последовательным соединением элементов, когда ток в цепи совпадает по фазе с напряжением источника.
Найдем условия резонанса напряжений. Для того чтобы ток в цепи совпадал по фазе с напряжением, реактивное сопротивление должно равняться нулю, так как
tg j = X / R = (XL - XC) / R.
Таким образом, условием резонанса напряжений является равенство реактивного сопротивления цепи нулю, или
XL = XC.
Но XL = wL, а XC = 1 / wС, где w - частота источника питания. В результате можно записать:
wL = 1 / wС.
Решая это уравнение относительно w находим:
w = 1 / (L×C)1/2 = w0.
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Резонансу напряжений соответствует векторная диаграмма:
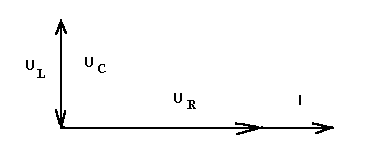
На основании этой диаграммы и закона Ома для этой цепи сформулируем признаки резонанса напряжений:
1. полное сопротивление цепи минимально и чисто активное;
2. ток в цепи совпадает по фазе с напряжением источника и достигает максимального значения;
3. напряжение на катушке индуктивности равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах всей цепи (в 10 раз). Поэтому резонанс при последовательном соединении элементов называют резонансом напряжений.
Режим резонанса напряжений может быть получен изменением частоты напряжения источника при неизменных параметрах элементов колебательного контура или изменением параметров элементов колебательного контура.
В электроэнергетических устройствах в большинстве случаев резонанс напряжений - явление нежелательное, связанное с неожиданным возникновением перенапряжений, то есть напряжений в несколько раз превышающих рабочее напряжение установки, причем плавкие предохранители не защищают от возникновения этих перенапряжений.
Порядок выполнения работы.
1. Выбрать электроизмерительные приборы.
2. Собрать схему с активным, индуктивным и емкостным приемниками (узлы 1 и 2 собрать на наборном поле 23, Рис.1).
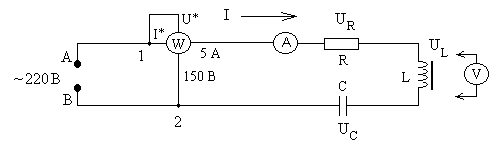
3. Включить схему после проверки ее преподавателем или лаборантом.
4. Снять показания амперметра и ваттметра и занести их в Таблицу 1. Вольтметром поочередно измерить падение напряжения на активном, индуктивном и емкостном приемниках и также занести в Таблицу 1.
Таблица 1.
| Измерено | |||||
| U | UR | UL | UC | I | P |
| В | В | В | В | А | Вт |
5. Показать преподавателю полученные экспериментальные результаты.
6. Разобрать электрическую схему и привести рабочее место в порядок.
7.Произвести вычисления, пользуясь при этом приведенными ниже формулами и заполнить
Таблицу 2.
Формулы для расчета:
| Z = U/I - полное сопротивление цепи; ZL = UL /I - полное сопротивление катушки; R = P/I2 - активное сопротивление цепи; RL= R - RR - активное сопротивление катушки; | UАL = UL×cosjL- активное напряжение катушки; UРL = UL×sinjL-реактивное напряжение катушки; | |
| RR = UR/I - активное сопротивление резистора; XL= (ZL2 -RL2)1/2 - индуктивное сопротивление катушки; L=XL/w - индуктивность катушки; w = 2pf - круговая частота; f = 50 Гц - частота; PL= I2RL - активная мощность катушки; QL = I2XL - реактивная мощность катушки; cos j = R/Z - коэффициент мощности цепи; cosjL=RL/Z- коэффициент мощности катушки; | XC=UC/I-реактивное сопротивление конденсатора; QC=I2XC - реактивная мощность конденсатора; Q = QL - QC - реактивная мощность цепи; X = XL - XC - реактивное сопротивление цепи; C= 106/2pfXC - емкость конденсатора (в мкФ). | |
Таблица 2.
| Вычислено | |||||||||||||||||
| Z | ZL | RR | R | RL | XL | L | QL | PL | cosj | cos jL | UАL | UРL | XC | X | C | QC | Q |
| Ом | Ом | Ом | Ом | Ом | Ом | Гн | вар | Вт | - | - | В | В | Ом | Ом | мкФ | вар | вар |
8. По вычисленным данным построить в масштабе векторную диаграмму напряжений.
9. Определить резонансную частоту, учитывая рассчитанные индуктивность и емкость
приемников.
Контрольные вопросы.
1. Преимущества электрической энергии перед другими видами энергии.
2. Электрическая цепь. Контур. Узел электрической цепи. Принципиальные схемы.
3. Электрический ток. Сила тока. Единица измерения. Постоянный ток. Переменный ток.
4. Электродвижущая сила. Напряжение. Единица измерения.
5. Электрическое сопротивление. Единицы измерения. Природа электрического сопротивления проводников.
6. Режимы работы электрической цепи.
7. Мгновенные значения силы тока, напряжения и Э.Д.С. Амплитудное значение.
8. Фаза, начальная фаза. Период, частота, угловая частота. Единицы измерения.
9. Действующее значение. Связь амплитудного и действующего значений. Амплитудное значение напряжения в осветительной сети.
10.Активное сопротивление. Резистор. Активная мощность.
11.Природа различия между активным и реактивным сопротивлением. Реактивные сопротивления.
12.Зависимость активного и реактивного сопротивления от частоты переменного тока.
13.Законы Кирхгофа для цепей переменного тока.
14.Последовательный колебательный контур.
15.Полное сопротивление цепи. Закон Ома для последовательного колебательного контура.
16.Векторные диаграммы для электрической цепи с активным, емкостным и индуктивным приемниками.
17.Энергетические процессы протекающие в цепях с активным, индуктивным и емкостным приемниками.
18.Энергетические характеристики: активная, реактивная и полная мощности. Единицы измерения.
19.Треугольники напряжений, сопротивлений и мощностей.
20.Фазовые соотношения между токами и напряжениями на отдельных элементах цепи.
21.Коэффициент мощности и способы его повышения.
22.Резонансные явления в цепях переменного тока.
23.Резонанс напряжений. Векторная диаграмма соответствующая резонансу напряжений.
24.Признаки резонанса напряжений. Резонансная частота.
Литература.
1. Электротехника. Конспект лекций для специальности. С.Н. Самсоненко, Н.Д. Самсоненко, Н.И. Носанов. Макеевка, 2000, 105с.
2. Электротехника. Касаткин А.С., Немцов М.В. -М: «Энергоатомиздат», 1983, 480 с.
3. Электротехника. И.И.Иванов, В.С. Равдоник, -М.: «Высшая школа», 1984, 376с.