Численное дифференцирование

Аппроксимация производных. Напомним, что производной функции называется предел отношения приращения функции к соответствующему приращению аргумента при стремлении к нулю:

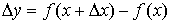, . (4.1)

Обычно для вычисления производных используют готовые формулы (таблицу производных) и к выражению (4.1) не прибегают. Однако в численных расчетах на компьютере использование этих формул не всегда удобно и возможно. В частности, функция может быть задана в виде таблицы значений (полученных, например, в результате численного расчета). В таких случаях производную приближенно можно найти опираясь на формулу (4.1). Полагая равным некоторому конечному числу, получают приближенное равенство для вычисления производной

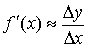. (4.2)

Это соотношение называется аппроксимацией (приближением) производной с помощью конечных разностей (значения и в формуле (4.2) конечны в отличие от их бесконечно малых значений в (4.1)).

Соотношение (4.2) может быть использовано для приближенного вычисления производной от функции, заданной как аналитическим выражением, так и таблично. В первом случае выбор величины произволен и определяется характером поведения функции. Для получения хорошей точности величину выбирают достаточно малой, такой чтобы на интервале функция была бы монотонна и менялась не существенно. В случае, когда функция задана таблично, величина равна разности между соседними узлами таблицы в окрестности которых вычисляется производная. При этом, если количество узлов невелико и узлы расположены на большом расстоянии друг от друга, формула (4.2) может давать существенную погрешность. Вопросы оценки погрешностей, возникающих при численном дифференцировании, будут рассмотрен ниже.
Использование интерполяционных полиномов. Пусть в точках известны значения функции : . По табличным данным аппроксимируем функцию интерполяционным полином степени n:

.
Тогда для k -той производной от функции на отрезке интерполирования получим приближенную формулу

. (4.3)

Однако на практике редко прибегают к аппроксимации функции одним интерполяционным полиномом, т.е. к глобальной интерполяции, в частности, из-за свойственной ей большой погрешности. Как правило, пользуются локальной интерполяцией. При этом в окрестности точки, в которой нужно вычислить производную, функцию интерполируют полиномом невысокой степени (например, ).

Рассмотрим простейшие примеры. Пусть нужно вычислить производные функции в окрестности табличной точки . Для простоты будем считать, что табличные точки равноотстоят друг от друга, т.е. .

а) Приблизим в рассматриваемой окрестности функцию интерполяционным полиномом первой степени , т.е. прямой, проходящей через точки и :

Тогда

. (4.4)

С другой стороны в рассматриваемой окрестности функцию можно приблизить и так

В этом случае

. (4.5)

Мы получили простейшие приближенные формулы для первой производной от функции, заданной таблично. Формулу (4.5) называют левым разностным отношение м, а формулу (4.5) – правым разностным отношением. Смысл этих названий нетрудно понять из рисунка 4.1. Заметим, что эти соотношения можно было написать сразу, опираясь на формулу (4.2), полагая, например, 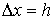и , и не привлекая интерполяцию в качестве промежуточного звена. Понятно также, что для получения приближенных формул для второй и высших производных линейного приближения функции недостаточно.

б) Приблизим в рассматриваемой окрестности функцию интерполяционным полиномом второй степени , т.е. параболой, проходящей через значения функции в точках :

.

Эта форма записи интерполяционного полинома несколько отличается о ньютоновской, которая была рассмотрена ранее в главе 3 при описании кусочно-квадратичной интерполяции (формула (3.12)). Такая форма записи является более компактной.

Дифференцируя это выражение один раз, получим новую приближенную формулу для первой производной:

. (4.6)

Здесь, в отличие от (4.4) и (4.5), приближение зависит от x. В частности, для имеем

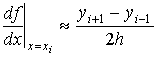. (4.7)

Это так называемое центральное разностное отношение. По сути оно определяет тангенс угла наклона прямой, проходящей через две табличные точки и .

Дифференцируя полином два раза, получаем приближенную формулу для второй производной:

. (4.8)

Аналогичным образом, привлекая интерполяцию полиномами более высокой степени, можно получать новые формулы для первой и второй производных, а также формулы для производных высших порядков.

Так, например, в случае интерполяции функции полиномом четвертой степени можно получить следующие формулы (центральные разностные соотношения) для первой и второй производной:

,

.
Погрешность численного дифференцирования. Основной источник погрешности, возникающей при численном дифференцировании связан с аппроксимацией функции . При использовании интерполяционных полиномов для аппроксимации функции имеем

,

где – ошибка интерполяции (остаточный член интерполирования). Следовательно погрешность вычисления производной функции по формуле (4.3) будет определяться производной от ошибки интерполяции .

Анализ погрешности формул численного дифференцирования, опирающийся на дифференцирование остаточного члена затруднен в силу математических сложностей. Поэтому мы познакомимся с другим подходом к анализу точности формул численного дифференцирования.

Прежде всего заметим, что все рассмотренные нами формулы для приближенного вычисления производной в конкретной точке имеют следующую структуру:

, (4.9)

где – постоянные коэффициенты; суммирование производится по некоторому диапазону табличных данных.
Анализ погрешности формулы (4.9) сводится к следующему. Заменяем все входящие в правую часть (4.9) значения по формулам Тейлора относительно точки, для которой рассматривается приближение (4.9). После проведения несложных арифметических преобразований в качестве главного члена правой части получаем приближенное значение производной. Остальные члены будут характеризовать погрешность.
В качестве примера рассмотрим оценку погрешности формулы (4.5) для точки . Заменим значения и по формулам Тейлора относительно точки x:

,

.
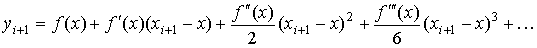Подставляя эти выражения в правую часть (4.5) получим

.
Таким образом, погрешность (ошибка) формулы (4.5) для произвольной точки будет определятся следующим выражением

Для точки получаем

, т.е. ,

следовательно, для формула (4.5) является формулой первого порядка точности¹²[1]. Можно показать, что для любой точки формула (4.5) также будет иметь первый порядок точности [8]. Исключение составляет точка – середина интервала , для которой

, т.е.

и, следовательно, в этом случае формула (4.5) является формулой второго порядка точности.