Расчет прочности нормальных сечений.

 

Цель расчета - подбор продольной арматуры.

Характеристики прочности бетона и арматуры:

бетон:

класс – В15;

расчетное сопротивление осевому сжатию R_b=8.5 МПа;

расчетное сопротивление осевому растяжению R_bt=0.75 МПа;

модуль упругости бетона E_b=24×10³ МПа;

γ_b2=0.9

арматура:

поперечная Æ5 класс Вр-I

расчетное сопротивление растяжению арматуры R_s=260 МПа;

продольная A-III

расчетное сопротивление растяжению арматуры R_s=365 МПа;

модуль упругости стали арматуры E_s=200×10³ МПа;

Рис.18

1. Подбор арматуры сечение в первом пролете по М₁

Расчет производится по алгоритму таврового профиля с шириной полки а₁=1,67 м, толщиной полки δ=6 см и высотой h_вб=40 см

M₁=39758,66 Н·м h₀=h-а_з=40-3,5=36,5 см

α_m=M₁/(R_b×b_f^`×h₀²×0.9×(100))=3975866/(8.5×167×36,5²×0.9×(100)) =0,02

ξ=0.02 x=ξ×h₀=0.02×36,5=0,73см < 10 см

ζ=0.99

A_S=M₁/(R_s×ζ×h₀)=5761000/(365×100×0.99×36.5)=3.01 см²

Принимаем AIII 2Æ14 A_Sb=3,08 см²

2. Подбор арматуры в пролете по М₃

h₀=h-а_з=40-4=36 см

M₃=27334,08 Н×м

α_m=M₃/(R_b×b×h₀²×0.9×(100))=2733408 /(8.5×167×36,5²×0.9×100) =0.02

ξ=0.02 x=ξ×h₀=0.02×36,5=0,73см < 10 см

ζ=0.99

A_S=M₃/(R_s×ζ×h₀)=2733408/(365×100×0.99×36,5)=2,07 см²

Принимаем AIII 2Æ12 A_S=2,26см²

3. На отрицательный момент сечение работает как прямоугольное.

M_0.25=7809,7375 Н×м

α_m=М_0.25/(R_b×b×h₀²×0.9×(100))=780973,75 /(8.5×167×36,5²×0.9×100) =0,005

ξ=0.01

ζ=0.995

A_S=M_0.25/(R_s×ζ×h₀)=780973,75 /(365×100×0.995×36,5)=0,589 см²

Принимаем AIII 2Æ8 A_S=1,01 см²

4. Сечение на первой промежуточной опоре.

M_В=31238,95 Н×м

α_m=М_В/(R_b×b×h₀²×0.9×(100))=3123895/(8.5×167×36,5²×0.9×100) =0,02

ξ=0.02

ζ=0.99

A_S=M_В/(R_s×ζ×h₀)=3123895/(365×100×0.99×36,5)=2,37 см²

Принимаем AIII 6Æ8 A_S=3,02 см² две гнутые сетки по 3Æ6 AIII в каждой.

5. Подбор арматуры в среднем пролете.

М_С=М_Д=27334,08Н×м

α_m=М_СД/(R_b×b×h₀²×0.9×(27334,08/(8.5×167×36,5²×0.9×100) =0.02

ξ=0.02

ζ=0.99

A_S=M₃/(R_s×ζ×h₀)=2733408/(365×100×0.99×36,5)=2,07 см²

Принимаем AIII 5Æ8 A_S=2,51 см²

 

Расчет прочности наклонных сечений.

Q_max =38875,14 Н

Диаметр поперечных стержней устанавливаем из условия сварки с продольными стержнями d=14 мм принимаем d_sw=5мм класса Вр-I R_sw=260 МПа число каркасов –2, A_sw=2×0.196=0.392 см²

Шаг поперечных стержней по конструктивным условиям S=h/2=30/2=15см

В средней части пролета (L/2) S=3/4h=3/4·40=30 см

q_sw=R_sw×A_sw/s=260×0.392×(100)/15=680 H/см

Влияние свесов сжатой полки:

см;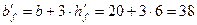

Q_bmin=φ_b3×(1+φ_f) ×R_bt×b×h₀

Q_bmin=0.6×1,11×0.9×0.75×20×36,5×(100)=32000Н

Условие Q_max< Q_bmin выполняется 38875,14>32000

S_max=φ_b4×R_bt×b×h₀²/Q_max=1.5×0.9×0.75×20×36,5²×(100)/38875,14=69,4см>30см-удовлетворяет

q_sw=R_sw·A_sw/S

q_sw ≥Q_bmin/(2h₀)

679.5>32000/2·36,5=397 Н/см

M_В=φ_b6×K×R_bt×b×h₀²=2×1.11×0.9×0.75×20×36,5²×(100)=4436392,5 H×см

q₁=q+V/2=77,04 Н/см

Условие q₁<0.56×q_sw выполняется 77,040 <0,56·679,5=380,52 H/см

Находим значение с:

239> (2/0,6)36,5=121 –условие выполняется с=121 см.

Тогда: Q_b=M_В/c=4436392,5/121=36664 Н>Q_bmin=32000 Н

Условия: с₀<c 81<121-выполняется

с₀<2h₀ 81<73 – выполняется с₀=73

Q­_sw=q_sw×c₀=679,5×73=49603,5 H

c₀-длина проекции расчетного наклонного сечения

Поперечная сила в вершине сечения (наклонного):

Q=Q_max – q₁×c=38875,14-7704×1,21=29553,3 Н

Условие прочности:

Q<Q_b+Q_sw

29553,3<36664+49603,5=86267,5 Н – условие выполнено.

Проверка по сжатой наклонной полосе

μ_sw=A_sw/(b×s)=0.392/(20×30)=0.0007

α=E_s/E_b=170000/2300=7.4

φ_w1=1+5×α×μ_w1=1+5×7.4×0.0007=1.03<1.3

φ_b1=1-0.01R_bt=1-0.01×0.75=0.9925

Условие:

Q_max<0.3×φ_w1×φ_b1×R_b×b×h₀

Q_max<0.3×1.03×0.9925×8.5×100×20×36.5=190296.5 H

38875.14<190296.5 –условие выполнено.

 

 

Список использованной литературы.

 

1 СНиП 2.03.01-84. Бетонные и железобетонные конструкции / Госстрой СССР. – М.: ЦИТП Госстроя СССР,1985.- 79с.

2. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий курс: Учебник для вузов. – М.: Стройиздат, 1991.-767с.

3.СНиП 2.01.07-85. Нагрузки и воздействия / Госстрой СССР. – М.: ЦИТП Госстроя СССР,1986.- 36с.

4.Жаркова Н.Н. Методические указания к расчету железобетонных панелей перекрытий многоэтажных здание на персональных ЭВМ.- Владивосток: ДВПИ, 1987.- 24с.

5.Жаркова Н.Н. Игнатенко Т.К. Методические указания к курсовому проекту - Владивосток: ДВГТУ, 1996.- 32с.