СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ПЛАН ЛЕКЦИИ
I. Понятие случайной величины
II. Числовые характеристики случайных величин
III. Законы распределения дискретных случайных величин
I. Понятие случайной величины. Случайной называется величина, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Будем обозначать случайные величины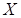 
, 
, 
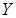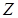, а их возможные значения – 
, 
, 
.
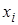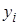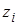Дискретной (или прерывной) называется случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным).
Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.
Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
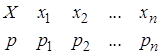. (1)
В одном испытании случайная величина принимает одно и только одно возможное значение, поэтому события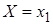 
, 
, …, 
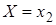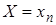образуют полную группу. Следовательно, сумма вероятностей этих событий равна единице:
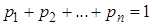. (2)
Пример 1. В лотерее участвует 100 билетов. Разыгрывается 5 выигрышей по 300 рублей, 10 выигрышей по 200 рублей и 25 выигрышей по 100 рублей. Найти закон распределения случайной величины 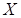– размера возможного выигрыша для владельца одного билета.
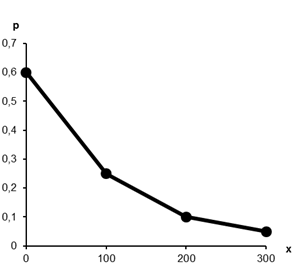
Решение. Случайная величина 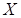может принимать следующие возможные значения: 0, 100, 200, 300. Вероятности этих возможных значений 0,6; 0,25; 0,1 и 0,05 соответственно. Тогда закон распределения случайной величины 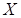имеет вид:
, 
.
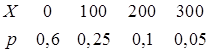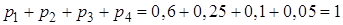Для наглядности закон распределения дискретной случайной величины можно изобразить графически. Для этого в прямоугольной системе координат строят точки с координатами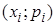 
, а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Пример 2. Построить многоугольник распределения для закона распределения из примера 1.
II. Числовые характеристики случайных величин. Часто закон распределения случайной величины бывает неизвестен, и приходится пользоваться числами, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайных величин.
Основными числовыми характеристиками дискретных и непрерывных случайных величин являются математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:
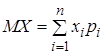или 
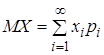. (3)
Первая из формул (3) справедлива для конечного числа возможных значений дискретной случайной величины, вторая – для бесконечного. Математическое ожидание является неслучайной (постоянной) величиной.
Пусть вероятность события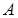 
равна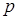 
. Случайная величина 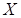– число появлений события 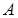в одном испытании – может принимать два значения: 
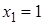(событие 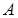наступило) с вероятностью 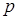и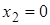 
(событие 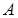не наступило) с вероятностью 
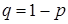. Математическое ожидание такой случайной величины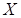 
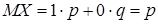, то есть математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Размерность математического ожидания совпадает с размерностью случайной величины .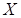
Свойства математического ожидания:
1) математическое ожидание постоянной величины равно самой постоянной величине,
, 
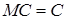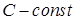; (4)
2) постоянный множитель можно выносить за знак математического ожидания,
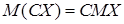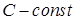, ; (5)
3) для формулировки следующего свойства математического ожидания дадим определения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные. Определим произведение независимых случайных величин 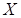и 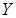как случайную величину 
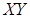, возможные значения которой равны произведениям каждого возможного значения случайной величины 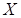на каждое возможное значение случайной величины 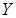. Вероятности возможных значений произведения 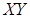равны произведениям вероятностей возможных значений множителей. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий,
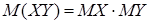. (6)
Следствие свойства 3: математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий,
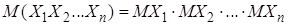; (7)
4) определим сумму случайных величин 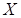и 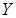как случайную величину 
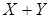, возможные значения которой равны сумме каждого возможного значения случайной величины 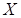и каждого возможного значения случайной величины 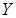. Вероятности возможных значений случайной величины 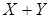для независимых величин 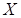и 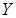равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность другого. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых,
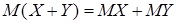. (8)
Следствие свойства 4: математическое ожидание суммы нескольких взаимно независимых случайных величин равно сумме их математических ожиданий,
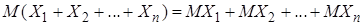. (9)
Отклонением называется разность между случайной величиной и ее математическим ожиданием. Математическое ожидание отклонения случайной величины равно нулю:
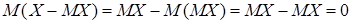. (10)
Центрированной случайной величиной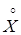 
называется разность между случайной величиной и ее математическим ожиданием:
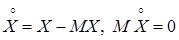. (11)
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
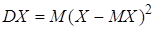. (12)
Дисперсия случайной величины является неслучайной (постоянной) величиной.
Теорема 1: дисперсия равна разности между математическим ожиданием квадрата случайной величины 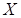и квадратом ее математического ожидания,
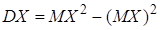. (13)
Доказательство.
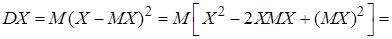
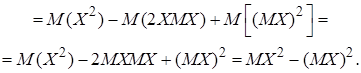
Теорема доказана.
Размерность дисперсии равна квадрату размерности случайной величины .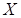
Свойства дисперсии:
1) дисперсия постоянной величины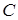 
равна нулю,
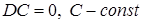; (14)
2) постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат,
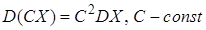; (15)
3) дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин,
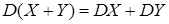. (16)
Следствия свойства 3:
а) дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин,
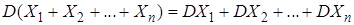; (17)
б) дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины,
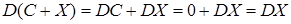; (18)
4) дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин,
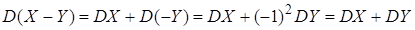. (19)
Средним квадратическим отклонением случайной величины 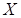называется квадратный корень из дисперсии:
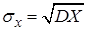. (20)
Среднее квадратическое отклонение является неслучайной (постоянной) величиной. Размерность среднего квадратического отклонения совпадает с размерностью случайной величины 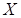. Поэтому в случаях, когда надо, чтобы оценка рассеяния имела размерность случайной величины, используется среднее квадратическое отклонение, а не дисперсия.
Теорема 2: среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин,
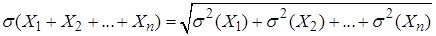. (21)
Доказательство.
По свойствам дисперсии (формула (17)), дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин
.
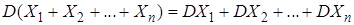Тогда
.
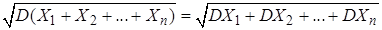Заменяя дисперсии под знаками радикалов на соответствующие квадраты средних квадратических отклонений, получим
.
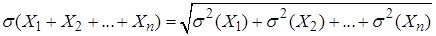Теорема доказана.