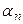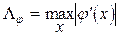Унифицированного формат представления нейросетевых моделей предложил Е.М. Миркес.
2.2.1. Функциональные компоненты. Основные функциональные компоненты нейрокомпьютера выделяются по следующим признакам:
1. Относительная функциональная обособленность: каждый компонент имеет четкий набор функций. Его взаимодействие с другими компонентами может быть описано в виде небольшого числа запросов.
2. Возможность реализации большинства используемых алгоритмов.
3. Возможность взаимозамены различных реализаций любого компонента без изменения других компонентов.
Краткий обзор нейронных сетей
Приведем классификацию нейронных сетей по решаемым ими задачам.
1. Классификация без учителя или поиск закономерностей в данных. Наиболее известным представителем этого класса сетей является сеть Кохонена, реализующая простейший вариант решения этой задачи. Наиболее общий вариант решения этой задачи известен как метод динамических ядер.
2. Ассоциативная память. Наиболее известный представитель – сети Хопфилда. Эта задача также позволяет строить обобщения. Наиболее общий вариант описан в девятой главе.
3. Аппроксимация функций, заданных в конечном числе точек. К сетям, решающим эту задачу, относятся персептроны, сети обратного распространения ошибки.
Выделение компонент
Первым основным компонентом нейрокомпьютера является нейронная сеть. Относительно архитектуры сети принцип двойственности предполагает только одно – все элементы сети реализуют при прямом функционировании характеристические функции из класса 
(непрерывно дифференцируемые на области определения 
, которой, как правило, является вся числовая ось).
|
|
Для обучения нейронной сети необходимо наличие задачника. Однако чаще всего, обучение производится не по всему задачнику, а по некоторой его части. Ту часть задачника, по которой в данный момент производится обучение, будем называть обучающей выборкой. Для многих задач обучающая выборка имеет большие размеры (от нескольких сот до нескольких десятков тысяч примеров). При обучении с использованием скоростных методов обучения приходится быстро сменять примеры. Таким образом, скорость обработки обучающей выборки может существенно влиять на скорость обучения нейрокомпьютера.
При работе с обучающей выборкой удобно использовать привычный для пользователя формат данных. Однако, этот формат чаще всего непригоден для использования нейросетью. Таким образом, между обучающей выборкой и нейросетью возникает дополнительный компонент нейрокомпьютера – предобработчик. Из литературных источников следует, что разработка эффективных предобработчиков для нейрокомпьютеров является новой, почти совсем не исследованной областью.
Насколько привычный для человека способ представления входных данных непригоден для нейронной сети, настолько и формат ответов нейронной сети малопригоден для человека. Необходимо интерпретировать ответы нейронной сети. Интерпретация зависит от вида ответа. Так, если ответом нейронной сети является действительное число, то его, как правило, приходится масштабировать и сдвигать для попадания в нужный диапазон ответов. Если сеть используется как классификатор, то выбор интерпретаторов много шире. Большое разнообразие интерпретаторов при невозможности решить раз и навсегда вопрос о преимуществах одного из них над другими приводит к необходимости выделения интерпретатора ответа нейронной сети в отдельный компонент нейрокомпьютера.
|
|
С интерпретатором ответа тесно связан еще один обязательный компонент нейрокомпьютера – оценка. В ходе численных экспериментов было выяснено, что для обучения сетей-классификаторов функция оценки вида суммы квадратов отклонений выходного сигнала нейрона от ожидаемого, пожалуй, наиболее плоха. Использование функций оценки, построенных по интерпретатору ответа, позволяет в несколько раз ускорить обучение нейронной сети. Кроме того, использование интерпретаторов ответа и построенных по ним функций оценки с уровнем надежности, позволяет оценить степень уверенности нейронной сети в выданном ответе.
Шестым необходимым компонентом нейрокомпьютера является учитель. Этот компонент управляет процессом обучения и может иметь множество реализаций.
Принцип относительной функциональной обособленности требует выделения еще одного компонента, названного исполнителем запросов учителя или просто исполнителем. Назначение этого компонента не так очевидно, как всех предыдущих. Заметим, что для всех вариантов реализации компонента учитель, обучающих сети по методу обратного распространения ошибки, и при тестировании сети характерен один и тот же набор операций с каждым примером обучающей выборки. При этом необходима работа с сетью, задачником, интерпретатором ответа и оценкой. Таким образом, исполнитель исполняет всего один запрос – обработать пример. Однако выделение этого компонента позволяет исключить необходимость в прямых связях таких компонентов, как контрастер и учитель, с компонентами оценка и интерпретатор ответа, а их взаимодействие с компонентом сеть свести исключительно к запросам связанным с модификацией обучаемых параметров сети.
|
|
Последним компонентом, которого необходимо выделить, является контрастер нейронной сети. Этот компонент является надстройкой над учителем. Его назначение – сводить число связей сети до минимально необходимого или до «разумного» минимума (степень разумности минимума определяется пользователем). Кроме того, контрастер, как правило, позволяет свести множество величин весов связей к 2-4, реже к 8 выделенным пользователем значениям. Этот компонент нейрокомпьютера не предназначен для решения обычных задач нейроинформатики, поскольку он не используется ни при обучении, ни при тестировании нейронных сетей. Однако именно использование этого компонента делает нейрокомпьютер более полезным, чем обычные экспертные системы. Так основой контрастирования является метод оценивания значимости обучаемых параметров и сигналов нейронной сети. Этот метод дает ответ на один из наиболее важных для практиков вопросов – какие из входных сигналов играют важную роль в решении задачи, а какие фактически не влияют на ответ. Кроме того, процедура контрастирования позволяет выяснить, какой набор входных параметров является абсолютно необходимым для решения задачи. С точки зрения электронной реализации нейронных сетей особый интерес представляет возможность применения процедуры контрастирования для удаления «лишних» связей и уменьшения разрядности сигналов и параметров сети. Методика получения при помощи процедуры контрастирования логически прозрачных сетей – сетей, работу которых легко описать и понять на языке логики – позволяет частично решить одну из наиболее сложных проблем искусственного интеллекта – проблему получения явных знаний из данных.
Рис 2.1. Схема запросов в нейрокомпьютере
|
Для координации работы всех компонентов нейрокомпьютера вводится макрокомпонент Нейрокомпьютер. Основная задача этого компонента – организация интерфейса с пользователем и координация действий всех остальных компонентов.
На рис. 2.1 приведена схема взаимодействия различных компонентов в нейрокомпьютере. Стрелки, изображающие запросы, идут от объекта, инициирующего запрос, к объекту его исполняющему.
Задачник и обучающее множество. Важность этого компонента определяется тем, что при обучении сетей всех видов с использованием любых алгоритмов обучения сети необходимо предъявлять примеры, на которых она обучается решению задачи. Источником данных для сети является задачник. Кроме того, задачник содержит правильные ответы для сетей, обучаемых с учителем.
Обсуждение задачника. С точки зрения нейрокомпьютера задачник представляет собой прямоугольную таблицу, поля которой содержат информацию о входных данных примеров задачи, правильные ответы и другую информацию. Далее будем полагать, что задачник является реляционной базой данных. Каждому примеру соответствует одна запись базы данных. Каждому данному – одно поле. Все поля базы данных можно разбить на четыре типа – числовые поля, текстовые поля, перечислимые поля и поля типа рисунок.
Числовые поля. Поля числовых типов данных предназначены для хранения различных чисел. Поля числового типа могут нести любую смысловую нагрузку.
Перечислимые поля. Поля перечислимого типа служат для хранения качественных признаков – полей базы данных, содержащих, как правило, текстовую информацию, но имеющих малое число различных значений. Простейшим примером поля перечислимого типа является поле «пол. Поля перечислимого типа могут быть входными данными, комментариями или ответами.
Строки (текстовые поля). Поля текстового типа предназначены для хранения текстовой информации. Они могут быть только комментариями.
Рисунок. Поля типа рисунок предназначены для хранения графической информации. При передаче рисунков предобработчику используется формат, согласованный для предобработчика и задачника.
Компонент задачник является необходимой частью нейрокомпьютера вне зависимости от типа применяемых в нем нейронных сетей. Однако в зависимости от решаемой задачи содержимое задачника может меняться. Так, для решения задачи классификации без учителя используют нейросети, основанные на методе динамических ядер. Задачник для такой сети должен содержать только векторы входных данных и предобработанных входных данных. При использовании сетей, основанных на принципе двойственности, к задачнику необходимо добавить вектор правильных ответов. Кроме того, некоторые исследователи хотят иметь возможность просмотреть ответы, выданные сетью, вектор оценок примера, показатели значимости входных сигналов и, возможно, некоторые другие величины. Поэтому, стандартный задачник должен иметь возможность предоставить пользователю всю необходимую информацию.
Довольно часто при обучении нейронных сетей возникает необходимость использовать в обучении не все примеры задачника, а только часть. Например, такая возможность необходима при использовании метода скользящего контроля для оценки качества обучения сети.
Ту часть задачника, которая в данный момент используется в обучении нейронной сети, будем называть обучающей выборкой. Для выделения из задачника обучающей выборки разработан механизм «цветов». Все примеры покрашены в некоторые цвета. Обучающую выборку можно задать, указав цвета примеров, которые необходимо использовать в обучении.
Приведем классификацию полей базы данных по типу их использования в работе нейрокомпьютера.
Входные данные – совокупность полей содержащих информацию, необходимую для решения сетью примера. Поля входных данных могут быть: числом, полем с ограниченным числом состояний или рисунком.
Комментарии. Часто для идентификации примеров в задачнике необходимо использовать некоторые поля, содержащие идентификационную информацию (например, фамилию пациента). Для хранения идентификационной информации предназначен тип – комментарий. Поля комментарии не используются при обучении нейронных сетей. При необходимости исключить из множества входных данных какое-либо поле, то вместо реструктуризации всей базы достаточно объявить это поле комментарием.
Предобработанные данные – это набор полей, содержащих действительные числа, служащие входными сигналами сети. Предобработанные данные получаются из входных данных после предобработки, выполняемой компонентом предобработчик. Хранение предобработанных данных необязательно.
Правильные ответы – набор полей, содержащих ответы, которые должна выдать обученная нейронная сеть при решении примера. Правильные ответымогутчислами или полями с ограниченным набором состояний. В первом случае будем говорить о задаче аппроксимации функции, а во втором – о задаче классификации объектов.
Полученные ответы – набор полей для записи ответов, полученных в результате интерпретации ответа сети компонентом интерпретатор ответа.
Оценки – набор полей, содержащий оценки, полученные сетью за решение всех подзадач примера (число подзадач равно числу ответов примера).
Вес примера – поле типа действительное число, содержащее вес примера.
Достоверность ответа. Если при обучении сети используется оценка типа «расстояние до множества», то при вычислении оценки подзадачи примера уровень уверенности умножается на степень достоверности ответа. Достоверность ответа является набором полей типа действительное число со значениями от нуля до единицы, поскольку ответ каждой подзадачи данного примера может иметь свою достоверность.
Уверенность в ответе. При использовании некоторых видов оценки интерпретатор ответа способен оценить уверенность сети в полученном ответе. Группа полей уверенность в ответе служит для сохранения значений уверенности сети в ответах (для каждого ответа своя уверенность).
Физическая организация задачника не имеет существенного значения. Следует только предусмотреть возможность получения всей перечисленной выше информации.
В практической работе большинство таблиц данных не полны – часть данных в примерах задачника не известна. Задачник должен однозначно указать предобработчику неизвестные данные. Для этих целей для каждого типа входных данных определено специальное значение - неопределенное.
Предобработчик. Компонент предобработчик осуществляет предобработку входных данных для нейронных сетей. Для большинства нейронных сетей характерно наличие такого интервала входных сигналов, в пределах которого сигналы различимы. Для разных видов нейронов эти интервалы различны. Чаще всего можно пользоваться эмпирическим правилом: нейрон различает сигналы в том же диапазоне, в котором он генерирует выходной сигнал. Для сигмоидной сети это интервал [-1,1]. Опыт использования нейронных сетей с входными синапсами свидетельствует о том, что в подавляющем большинстве случаев предварительное масштабирование и сдвиг входных сигналов сильно облегчает обучение нейронных сетей.
Классификация компонентов входных данных. Информация поступает к нейронной сети в виде набора ответов на некоторый список вопросов. Можно выделить три основных типа ответов (вопросов): бинарный признак (возможен только один из ответов – истина или ложь); качественный признак (принимает конечное число значений); число.
Ответ типа качественный признак - это ответ с конечным числом состояний. Причем нельзя ввести осмысленное расстояние между состояниями. Примером качественного признака может служить состояние больного - тяжелый, средний, легкий.
Все качественные признаки можно в свою очередь разбить на три класса: упорядоченные признаки, неупорядоченные признаки, частично упорядоченные признаки.
Упорядоченным признаком называется такой признак, для любых двух состояний которого можно сказать, что одно из них предшествует другому. Тот факт, что состояние 
предшествует состоянию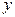 
, будем обозначать, как 
. Примером упорядоченного признака может служить состояние больного.
Признак называют неупорядоченным, если никакие два состояния нельзя связать естественным в контексте задачи отношением порядка.
Признак называется частично упорядоченным, если для каждого состояния существует другое состояние, с которым оно связано отношением порядка.
Известно, что любой частично упорядоченный признак можно представить в виде комбинации нескольких упорядоченных и неупорядоченных признаков. Исходя из этого, далее будет рассмотрено кодирование только упорядоченных и неупорядоченных признаков.
Таблица1.
Кодирование бинарного признака
|
Кодирование бинарных признаков. Бинарные признаки характеризуются наличием только двух состояний – истина и ложь. Однако даже такие простые данные могут иметь два разных смысла. Значение истина означает наличие у описываемого объекта какого-либо свойства. А ответ ложь может означать либо отсутствие этого свойства, либо наличие другого свойства. В зависимости от смысловой нагрузки значения ложь, и учитывая заданный диапазон 
, рекомендуемые способы кодирования бинарного признака приведены в табл. 1. Кодирование неупорядоченных качественных признаков. Поскольку никакие два состояния неупорядоченного признака не связаны отношением порядка, то было бы неразумным кодировать их разными величинами одного входного сигнала нейронной сети. Для кодирования качественных признаков рекомендуется использовать столько входных сигналов, сколько состояний у этого качественного признака. Так если набор всех состояний рассматриваемого признака обозначить через 
, то рекомендуемая таблица кодировки имеет вид, приведенный в табл.2.
Таблица 2.
Кодирование неупорядоченного качественного признака
|
Кодирование упорядоченных частных признаков. Упорядоченные частные признаки, в отличие от неупорядоченных, имеют отношение порядка между состояниями. Однако кодирование их разными значениями одного входного сигнала некорректно из-за того, что расстояние между состояниями не определено, а такое кодирование эти расстояния задает явным образом. Поэтому, упорядоченные частные признаки рекомендуется кодировать в виде стольких входных сигналов, сколько состояний у признака. Но, в отличие от неупорядоченных признаков, накапливать число сигналов с максимальным значением. Для случая, когда все состояния обозначены через 
, рекомендуемая таблица кодировки приведена в табл.3.
Таблица 3.
Кодирование упорядоченного качественного признака
|
Числовые признаки. При предобработке численных сигналов необходимо учитывать содержательное значение признака, расположение значений признака в интервале значений, точность измерения значений признака.
Содержательное значение признака. Если входными данными сети является угол между двумя направлениями, например, направление ветра, то не следует подавать на вход сети значение угла, поскольку это ведет к необходимости «уяснения» сетью того факта, что 0 градусов и 360 градусов одно и тоже. Рекомендуется подавать в качестве входных данных синус и косинус этого угла. Число входных сигналов сети увеличивается, но зато близкие значения признака кодируются близкими входными сигналами.
Точность измерения признака. В метеорологии используется всего восемь направлений ветра. Значит, при подаче входного сигнала сети необходимо подавать не угол, а всего лишь информацию о том, в какой из восьми секторов этот угол попадает. Таким образом направление ветра не числовой параметр, а неупорядоченный качественный признак с восемью состояниями.
Расположение значений признака в интервале значений. Следует рассмотреть вопрос о равнозначности изменения значения признака на некоторую величину в разных частях интервала значений признака. Как правило, это связано с косвенными измерениями. Например, сила притяжения двух небесных тел при условии постоянства массы однозначно характеризуется расстоянием между ними. Однако на вход сети лучше подавать не расстояние, а обратный квадрат расстояния 
.
Простейшая предобработка числовых признаков. Числовые сигналы рекомендуется масштабировать и сдвигать так, чтобы весь диапазон значений попадал в диапазон приемлемых входных сигналов. Эта предобработка проста и задается следующей формулой:
, (1)
где - диапазон приемлемых входных сигналов, 
– диапазон значений признака 
, 
– предобработанный сигнал, для подачи сети. Предобработку входного сигнала по формуле (1) будем называть простейшей предобработкой.
Оценка способности сети решить задачу. Предполагается, что все входные данные предобработаны так, что все входные сигналы сети лежат в диапазоне приемлемых входных сигналов . Пусть 
– векторы входных сигналов; 
– требуемые ответы сети. Компоненты векторов будем обозначать нижним индексом. Будем полагать, что в каждом примере ответ является вектором чисел из диапазона приемлемых сигналов . В случае обучения сети задаче классификации требуемый ответ зависит от вида используемого интерпретатора ответа.
Нейронная сеть вычисляет некоторую вектор-функцию 
от входных сигналов. Обучение сети состоит в подборе такого набора параметров сети, чтобы величина 
была минимальной (в идеале равна нулю). Для того, чтобы эта задача была принципиально разрешима, требуется, чтобы реализуемая сетью функция при изменении входных сигналов с на 
могла изменить значение с на 
. Наибольшую сложность будет представлять приближение функции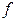 
в точках, в которых достигает максимума выражение 
. Для аналитически заданных функций величина 
называется константой Липшица. Получаем следующее определение сложности задачи.
Сложность аппроксимации таблично заданной функции 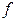, которая в точках принимает значения , задается выборочной оценкой константы Липшица (2).
(2)
Оценка (2) является оценкой константы Липшица аппроксимируемой функции снизу.
Для того, чтобы оценить способность сети заданной конфигурации решить задачу, необходимо оценить константу Липшица сети и сравнить ее с выборочной оценкой (2). Константа Липшица сети вычисляется по следующей формуле:
(3)
В формулах (2) и (3) можно использовать произвольные нормы, однако из соображений удобства в данной работе используется евклидова норма. Оценку константы Липшица сети строится в соответствии с принципом иерархического устройства. При этом потребуются следующие правила.
Для композиции функций 
константа Липшица оценивается как произведение констант Липшица:
. (4)
Для вектор-функции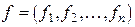 
константа Липшица равна:
. (5)
Таблица 4
|
В табл. 4 приведены значения констант Липшица для элементов, из которых конструируются нейронные сети.