Константа Липшица сигмоидной сети

Рассмотрим слоистую сигмоидную сеть со следующими свойствами: число входных сигналов – ; число нейронов в -м слое – ; каждый нейрон первого слоя получает все входные сигналы, а каждый нейрон любого другого слоя получает сигналы всех нейронов предыдущего слоя; все нейроны всех слоев являются сигмоидными и имеют одинаковую характеристику; все синаптические веса ограничены по модулю единицей; в сети слоев.

Учитывая формулы (4), (5) и табл.4 получаем оценку константы Липшица всей сети:

.

Для рассмотренных ранее сигмоидных нейронов 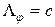и оценка константы Липшица сети равна

Эта формула подтверждает экспериментально установленный факт, что чем круче характеристическая функция нейрона (чем меньше c), тем более сложные функции (функции с большей константой Липшица) может аппроксимировать сеть с такими нейронами.

Предобработка, облегчающая обучение. При обучении нейронных сетей иногда возникают ситуации, когда дальнейшее обучение нейронной сети невозможно. В этом случае необходимо проанализировать причины. Возможно несколько видов анализа. Одной из возможных причин является высокая сложность задачи, определяемая как выборочная оценка константы Липшица. Для упрощения задачи необходимо уменьшить выборочную оценку константы Липшица. Далее описан ряд способов предобработки, уменьшающих сложность задачи.

Таблица 5. Кодирование параметра после разбиения на два сигнала Значение Первый сигнал Второй сигнал

Наиболее простой способ добиться этого – увеличить расстояние между входными сигналами. Рассмотрим пару примеров – , – таких, что . Определим среди координат векторов и координату, в которой достигает минимума величина , исключив из рассмотрения совпадающие координаты. Очевидно, что эта координата определяет сложность задачи. Следовательно, для уменьшения сложности задачи требуется увеличить расстояние между векторами и , а наиболее перспективной координатой для этого является -я. Зададимся точкой . Будем кодировать -й параметр двумя входными сигналами в соответствии с табл. 5. При таком кодировании критерий Липшица, очевидно, уменьшится. Наиболее эффективный путь выбора исходя из требования минимальности критерия Липшица.

Рассмотрим три вида предобработки числовых признаков – модулярный, позиционный и функциональный. Основная идея этих методов предобработки состоит в том, чтобы сделать значимыми малые отличия больших величин. Все эти виды предобработки обладают одним общим свойством – за счет кодирования входного признака несколькими сигналами они уменьшают сложность задачи (критерий Липшица).

Модулярная предобработка. Зададимся набором положительных чисел . Определим сравнение по модулю для действительных чисел следующим образом:

, (6)

где – функция, вычисляющая целую часть величины . Кодирование входного признака при модулярной предобработке вектором производится по следующей формуле:

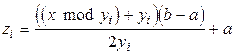. (7)

Модулярная предобработка полезна при предобработке признаков, у которых важна не абсолютная величина, а взаимоотношение этой величины с величинами .

Функциональная предобработка. Рассмотрим общий случай функциональной предобработки, отображающей входной признак в -мерный вектор . Возьмем чисел, удовлетворяющих следующим условиям: . Пусть – функция, определенная на интервале , а – минимальное и максимальное значения функции на этом интервале. Тогда -я координата вектора вычисляется по формуле:

(8)

Позиционная предобработка. Основная идея позиционной предобработки совпадает с принципом построения позиционных систем счисления. Зададимся положительной величиной 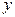такой, что . Сдвинем признак так, чтобы он принимал только неотрицательные значения. В качестве сигналов сети будем использовать результат простейшей предобработки 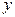-ичных цифр представления сдвинутого признака , формулы вычисления которых приведены ниже:

(9)

Составной предобработчик. Поскольку на вход нейронной сети обычно подается несколько входных сигналов, каждый из которых обрабатывается своим предобработчиком, то предобработчик должен быть составным. Представим предобработчик в виде совокупности независимых частных предобработчиков. Каждый частный предобработчик обрабатывает одно или несколько тесно связанных входных данных. На входе предобработчик получает вектор входных данных (возможно, состоящий из одного элемента), а на выходе выдает вектор входных сигналов сети (так же возможно состоящий из одного элемента).

Описание нейронных сетей. Один из важнейших компонентов нейрокомпьютера – нейронная сеть. Рассматриваются только сети, в которых все элементы каждого слоя срабатывают одновременно и затем передают свои сигналы нейронам следующего слоя.

Конструирование нейронных сетей. При описании нейронных сетей принято оперировать такими терминами, как нейрон и слой. Однако, при сравнении работ разных авторов выясняется, что если слоем все авторы называют приблизительно одинаковые структуры, то нейроны разных авторов совершенно различны. Таким образом, универсальное описание нейронных сетей на уровне нейронов невозможно. Однако, такое описание возможно на уровне составляющих нейроны элементов и процедур конструирования сложных сетей из простых. Впервые последовательное описание конструирования нейронных сетей из элементов было предложено А.Н. Горбанем в 1990 году. За прошедшее время предложенный А.Н. Горбанем способ конструирования претерпел ряд существенных изменений.

Элементы нейронной сети. На рис.2 приведены все элементы, необходимые для построения нейронных сетей. Естественно, что возможно расширение списка нелинейных преобразователей. Однако это единственный вид элементов, который может дополняться. Вертикальными стрелками обозначены входы параметров (для синапса – синаптических весов или весов связей), а горизонтальными – входные сигналы элементов. С точки зрения функционирования элементов сети сигналы и входные параметры элементов равнозначны. Различие между ними относятся к способу их использования в обучении. Кроме того, удобно считать, что параметры каждого элемента являются его свойствами и хранятся при нем. Совокупность параметров всех элементов сети называют вектором параметров сети. Необходимо различать входные сигналы элементов и входные сигналы сети. Они совпадают только для элементов входного слоя сети.

Из приведенных на рис. 2 элементов можно построить практически любую нейронную сеть. Вообще говоря, нет никаких правил, ограничивающих свободу творчества конструктора нейронных сетей. Однако есть набор структурных единиц построения сетей, позволяющий стандартизовать процесс конструирования. Детальный анализ различных нейронных сетей позволил выделить следующие структурные единицы: элемент – неделимая часть сети, для которой определены методы прямого и обратного функционирования; каскад – сеть, составленная из последовательно связанных слоев, каскадов, циклов или элементов; слой – сеть, составленная из параллельно работающих слоев, каскадов, циклов или элементов; цикл – каскад, выходные сигналы которого поступают на его собственный вход.

Очевидно, что не все элементы являются неделимыми. Часто вместо каскада из слоя синапсов и сумматора удобно использовать адаптивный сумматор.

Введение трех типов составных сетей связано с двумя причинами: использование циклов приводит к изменению правил остановки работы сети; разделение каскадов и слоев позволяет эффективно использовать ресурсы параллельных ЭВМ. Все сети, входящие в состав слоя, могут работать независимо друг от друга. Тем самым при конструировании сети автоматически закладывается база для использования параллельных ЭВМ.

На рис. 3 приведен пример поэтапного конструирования трехслойной сигмоидной сети.

Составные элементы. Название «составные элементы» противоречит определению элементов. Это противоречие объясняется соображениями удобства работы. Введение составных элементов упрощает конструирование нейронных сетей. Как правило, составные элементы являются каскадами простых элементов. В ряде работ интенсивно используются сети, нейроны которых содержат нелинейные входные сумматоры. Под нелинейным входным сумматором, чаще всего понимают квадратичные сумматоры – сумматоры, вычисляющие взвешенную сумму всех попарных произведений входных сигналов нейрона. Отличие сетей с квадратичными сумматорами заключается только в использовании этих сумматоров. На рис. 4 представлены схемы и обозначения для нескольких составных элементов. При составлении сети с квадратичными сумматорами из простых элементов на пользователя ложится большой объем работ по проведению связей и организации вычисления попарных произведений.

Кроме того, схема с использованием обозначений квадратичных сумматоров понятнее и содержит ту же информацию. Кроме того, пользователь может изменить тип сумматоров уже сконструированной сети, указав замену одного типа сумматора на другой. Легко показать, что неоднородные сумматоры (рис. 4) обеспечивают большую гибкость в работе.

Функционирование сети. Прежде всего, необходимо разделить процессы обучения и использования нейронной сети. При использовании обученной сети происходит только решение сетью определенной задачи. При этом обучаемые параметры сети остаются неизменными. Этот режим будем называть прямым функционированием.

При обучении нейронных сетей методом двойственности нейронная сеть (и каждый составляющий ее элемент) должна уметь выполнять обратное функционирование. Можно показать, что обратное функционирование позволяет обучать также и нейросети, традиционно считающиеся не обучаемыми, а формируемыми (например, сети Хопфилда). Обратным функционированием называется процесс работы сети, в ходе которого на выходах обратного функционирования вычисляются поправки к обучаемым параметрам. В случае сетей с непрерывно дифференцируемыми элементами вектор поправок является вектором градиента.

Три метода построения сетей для обратного функционирования.

Рис. 5 Прямое ненагруженное (а) и прямое нагруженное и обратное (б) функционирование сети.

А.Н. Горбань предложил метод построения сети, двойственной к данной. Е.М. Миркес предложил два других метода, решающих ту же задачу. Рассмотрим все три метода.

Рис.6 Фрагменты исходной (верхний ряд) и двойственной (нижний ряд) сети для синапса и нелинейного преобразователя

На рис. 5а приведена схема некоторой нейронной сети. На рис. 5б приведена схема той же сети и двойственной к ней (двойственная получает ряд сигналов из первоначальной сети). Этот метод построения двойственных сетей имеет ряд недостатков. С одной стороны, каждый элемент сети, кроме сумматора и точки ветвления, должен распознавать как минимум три режима работы: простое прямое функционирование, нагруженное прямое функционирование и обратное функционирование. В каждом из этих режимов элемент выполняет разные действия. Кроме того, если возникает необходимость вычисления производных некоторого функционала от градиента, то потребуется дважды двойственная сеть. В этом случае элементы сети обязаны уметь выполнять еще и дважды нагруженное функционирование, а архитектура сети еще более усложняется. Если строить трижды двойственную сеть, то у элементов возникают трижды нагруженное функционирование и т.д. Однако основной сложностью построения двойственной, дважды двойственной и т.д. сетей является сложность построения архитектуры таких сетей, поскольку при построении дважды двойственной сети строится не сеть, двойственная к двойственной сети, а именно дважды двойственная сеть.

Е.М. Миркес предложил другой способ построения двойственной (дважды, трижды и т.д.) сети. Основная идея этого метода состоит в унификации процедуры получения двойственной сети из исходной. Каждый элемент исходной сети заменяется в двойственной сети на двойственную ему подсеть. Кроме того, каждая двойственная подсеть получает все входные элементы, которые получал элемент исходной сети. Для простого сумматора двойственная подсеть – точка ветвления и наоборот. При таком построении в двойственной сети больше элементов, чем в предложенном А.Н. Горбанем методе, но анализ сети показывает, что вычислений в сети производится точно столько же. Кроме того, элементы в данном методе проще, поскольку каждый элемент выполняет только функционирование вперед. На рис. 6 приведены два фрагмента исходной и двойственной сети. Очевидно, что при использовании данного метода построение дважды двойственной сети – это построение сети двойственной к двойственной; трижды двойственной сети – двойственной к дважды двойственной и т.д. Недостатком этого метода является необходимость определять для каждого нелинейного преобразователя двойственный к нему элемент, дважды двойственный и т.д.

Однако с точки зрения электронной реализации, оба этих метода обладают одним общим недостатком – для реализации обратного функционирования необходимо изменять архитектуру сети, причем в ходе обратного функционирования связи прямого функционирования не используются. Исходя из этого соображения, Е.М. Миркес предложил метод самодвойственных сетей. Этот метод не позволяет строить дважды двойственных сетей, что делает его менее мощным, чем два предыдущих. Однако большинство методов обучения не требует использования дважды двойственных сетей, что делает это ограничение не очень существенным. Элементы должны исполнять два вида действий – прямое и обратное функционирование, что делает элементы более сложными, чем во втором методе, но более простыми, чем в первом. Основным достоинством данного метода является использование при прямом и обратном функционировании одних и тех же связей, что с точки зрения электронной реализации дает огромное преимущество перед двумя другими методами. Далее в данной работе рассматриваются только самодвойственные сети.

Если на выход сети с непрерывными элементами подается производная некоторой функции F от выходных сигналов сети, то вычисляемые сетью поправки должны быть элементами градиента функции F по обучаемым параметрам сети. Исходя из этого требования, определим правила обратного функционирования для элементов сети: при обратном функционировании на каждый вход элемента будет передаваться сигнал, равный произведению сигнала обратного функционирования на производную выходной функции элемента по сигналу (параметру) данного входа. Ниже приведены сигналы обратного функционирования для элементов, приведенных на рис.2.

У синапса два входа – вход сигнала и вход синаптического веса. Обозначим входной сигнал синапса через , а синаптический вес через . Тогда выходной сигнал синапса равен . При обратном функционировании на выход синапса подается сигнал . На входе синапса должен быть получен сигнал обратного функционирования, равный 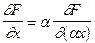, а на входе синаптического веса – поправка к синаптическому весу, равная .

Умножитель, с точностью до обозначений, полностью аналогичен синапсу.

Точка ветвления при обратном функционировании работает как сумматор.

Сумматор при обратном функционировании переходит в точку ветвления.

Нелинейный Паде-преобразователь имеет два входных сигнала и один выходной . При обратном функционировании на выход Паде-элемента подается сигнал . На входах сигналов и должны быть получены сигналы обратного функционирования, равные и .

Нелинейный сигмоидный преобразователь имеет один входной сигнал и один параметр . Выходной сигнал равен 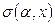. При обратном функционировании на выход сигмоидного элемента подается сигнал . На входе сигнала должен быть получен сигнал обратного функционирования, равный , а на входе параметра – поправка, равная .

Пороговый преобразователь, реализующий функцию определения знака, не является элементом с непрерывной функцией, и, следовательно, его обратное функционирование не может быть определено из требования вычисления градиента. Однако при обучении сетей с пороговыми преобразователями полезно иметь возможность вычислять поправки к параметрам. Доопределим его, исходя из соображений полезности при конструировании обучаемых сетей. Основным методом обучения сетей с пороговыми элементами является правило Хебба. Оно состоит из двух процедур, состоящих в изменении «весов связей между одновременно активными нейронами». Для этого правила пороговый элемент при обратном функционировании должен выдавать сигнал обратного функционирования, совпадающий с выданным им сигналом прямого функционирования. Такой пороговый элемент будем называть зеркальным. При обучении сетей Хопфилда, необходимо использовать «прозрачные» пороговые элементы, которые при обратном функционировании пропускают сигнал без изменения.

Правила остановки работы сети. При использовании сетей прямого распространения (сетей без циклов) вопроса об остановке сети не возникает. Сложнее обстоит дело при использовании сетей с циклами. В случае общего положения, после подачи сигналов на входные элементы сети по связям между элементами, входящими в цикл, ненулевые сигналы будут циркулировать сколь угодно долго.

Существует два основных правила остановки работы сети с циклами. Первое правило состоит в остановке работы сети после указанного числа срабатываний каждого элемента. Циклы с таким правилом остановки будем называть ограниченными. Второе правило остановки работы сети – сеть прекращает работу после установления равновесного распределения сигналов в цикле. Такие сети будем называть равновесными. Примером равновесной сети может служить сеть Хопфилда.

Архитектуры сетей. Как уже отмечалось ранее, при конструировании сетей из элементов можно построить сеть любой архитектуры. Однако и при произвольном конструировании можно выделить наиболее общие признаки, существенно отличающие одну сеть от другой. Замена простого сумматора на адаптивный или на квадратичный не приведут к существенному изменению структуры сети, хотя число обучаемых параметров увеличится. Однако введение в сеть цикла изменяет как структуру сети, так и ее поведение. Таким образом, все сети можно разбить на два класса: ациклические сети и сети с циклами. Среди сетей с циклами существует еще одно разделение, влияющее на способ функционирования сети: равновесные сети с циклами и сети с ограниченными циклами.

Особо отметим архитектуру еще одного класса сетей – сетей без весов связей. Эти сети, в противовес коннекционистским, не имеют обучаемых параметров связей. Любую сеть можно превратить в сеть без весов связей заменой всех синапсов на умножители. Получится такая же сеть, только вместо весов связей будут использоваться сигналы. Таким образом, в сетях без весов связей выходные сигналы одного слоя могут служить для следующего слоя, как входными сигналами, так и весами связей. Вся память таких сетей содержится в значениях параметров нелинейных преобразователей. Из выше изложенного следует, что сети без весов связей способны вычислять градиент функции оценки и затрачивают на это ровно тоже время, что и аналогичная сеть с весами связей.

Модификация синаптической карты (обучение). Кроме прямого и обратного функционирования, все элементы должны уметь выполнять еще одну операцию – модификацию параметров. Процедура модификации параметров состоит в добавлении к существующим параметрам вычисленных поправок. Если обозначить текущий параметр элемента через , а вычисленную поправку через 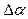, то новое значение параметра вычисляется по формуле 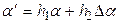. Параметры обучения и определяются компонентом учитель и передаются сети вместе с запросом на модификацию.

Во многих работах отмечается, что при описанной выше процедуре модификации параметров происходит неограниченный рост величин параметров. Наиболее простым решением этой проблемы является жесткое ограничение величин параметров некоторыми минимальным и максимальным значениями. В случае выхода значения параметра за заданный диапазон, его значение полагается равным ближайшей границе диапазона.

Контрастирование и нормализация сети. При контрастировании сети многие веса связей заменяются нулями. Очевидно, что при высокой степени разреженности ненулевых параметров проводить вычисления так, как будто структура сети не изменилась, неэффективно. Возникает потребность в процедуре нормализации сети, то есть фактического удаления нулевых связей из сети. Процедура нормализации состоит из двух этапов: из сети удаляются все связи, имеющие нулевые веса и исключенные из обучения; из сети удаляются все подсети, выходные сигналы которых не используются другими подсетями в качестве входных сигналов и не являются выходными сигналами сети в целом.

Оценка и интерпретатор ответа. Этот пункт посвящен двум тесно связанным компонентам нейрокомпьютера – оценке и интерпретатору ответа. Первичным из этих двух компонентов является интерпретатор ответа. Основное назначение этого компонента – интерпретировать выходные сигналы нейронной сети, являющиеся вектором действительных чисел, так, что бы ответ стал понятен пользователю. Если в качестве ответа ожидается действительное число, то интерпретация сводится к масштабированию и сдвигу. В случае решения задачи классификации многообразие интерпретаторов ответа существенно шире. Как правило, задачу обучения нейронных сетей можно формулируют следующим образом: необходимо подобрать такие значения обучаемых параметров нейронной сети, чтобы достигался минимум функции оценки. На самом деле правильная постановка задачи имеет вид: необходимо подобрать такие значения обучаемых параметров нейронной сети, чтобы результат интерпретации ответов совпадал с правильными ответами. На первый взгляд различие между этими постановками невелико, но вторая постановка позволяет сформулировать главный принцип построения оценки: функция оценки должна достигать минимума в таких точках пространства параметров, в которых результат интерпретации ответов нейронной сети совпадает с правильными ответами для всех примеров обучающего множества.

На практике, в качестве точки минимума функции оценки задают такую точку в пространстве выходных сигналов нейронной сети, в которой правильная интерпретация гарантирована, а затем строят оценку как сумму квадратов уклонений полученных выходных сигналов нейронной сети от заданной точки минимума. Такой подход универсален и прост, но накладывает на нейронную сеть чересчур жесткие требования, поскольку обычно мощность множества точек, в которых происходит правильная интерпретация – континуум. Иными словами, при обучении нейронной сети используется достаточное условие, в то время как необходимое условие накладывает на выходные ответы нейронной сети существенно более слабые требования. Более того, в случае использования этой оценки пример с более надежной интерпретацией может иметь оценку хуже, чем пример с ненадежной интерпретацией.

Процедура построения оценки по интерпретатору ответа состоит из следующих этапов.

Определяем множество правильно интерпретируемых точек в пространстве выходных сигналов нейронной сети.

Строим проектор произвольной точки пространства выходных сигналов нейронной сети на это множество.

В качестве функции оценки выбираем расстояние от точки выходных сигналов нейронной сети до проекции этой точки на множество правильных ответов.

Оценки такого вида получили название оценок типа «расстояние до множества». Если необходимо получить сеть, устойчивую к изменению выходного сигнала нейронной сети на e, то при определении множества правильных ответов следует считать правильными только те точки, которые правильно интерпретируются даже при изменении любого выходного сигнала нейронной сети на e. Величину e будем называть уровнем надежности.

В качестве примера рассмотрим максимальный интерпретатор. Нейросеть выдает вектор из N сигналов. Номер нейрона, выдавшего максимальный по величине сигнал, является номером класса, к которому относится предъявленный сети входной вектор. Пусть для рассматриваемого примера правильным ответом является k -ый класс. Тогда множество правильных ответов задается следующей системой неравенств: при . Исключим из вектора выходных сигналов сигнал , а остальные сигналы отсортируем по убыванию. Обозначим величину через 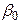, а вектор отсортированных сигналов через . Множество правильных ответов имеет вид , при i> 0. Найдем минимальное l, такое, что верно неравенство . Если такого l нет, то положим его равным N- 1. Оценка равна следующей величине

.

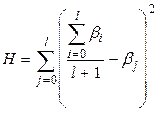Уровень уверенности. Часто при решении задач классификации с использованием нейронных сетей недостаточно простого ответа «входной вектор принадлежит K- муклассу». Необходимо также оценить уровень уверенности в этом ответе. Для различных интерпретаторов вопрос определения уровня уверенности решается по-разному. Однако от нейронной сети нельзя требовать больше того, чему ее обучили. При обучении с использованием оценки типа расстояние до множества, уровень надежности позволяет строить оценку уровня уверенности сети. При решении примера получены выходные сигналы. Уровнем уверенности сети в ответе называется отношение минимальной величины, на которую надо изменить один из выходных сигналов для изменения результата интерпретации, к уровню надежности, использованному при обучении.

Для максимального интерпретатора – , где – максимальный, а – второй по величине сигналы.

Для ответа типа число, ввести уровень уверенности подобным образом невозможно. Единственным способом оценки достоверности результата, в этом случае, является консилиум нескольких сетей: если несколько сетей обучены решению одной и той же задачи, то в качестве ответа можно выбрать среднее значение, а по отклонению ответов от среднего можно оценить достоверность результата.

Оценка обучающего множества. Вес примера.

Выше был рассмотрен ряд оценок, позволяющих оценить решение сетью конкретного примера. Однако основная задача при обучении нейронных сетей – обучить сеть решать все примеры обучающего множества. Ряд наиболее быстрых методов обучения, используют обучение по всей обучающей выборке. Поскольку градиент является линейным функционалом, то если положить оценку обучающего множества равной линейной комбинации оценок отдельных примеров, то и градиент оценки обучающего множества будет равен линейной комбинации градиентов оценок отдельных примеров с теми же коэффициентами:

Коэффициенты называют весами примеров. Использование в обучении сети механизма весов позволяет ускорит процесс обучения. Применение весов примеров может быть вызвано одной из следующих причин: один из примеров плохо обучается; число примеров разных классов в обучающем множестве сильно отличаются друг от друга; примеры в обучающем множестве имеют различную достоверность.

Под плохим обучением примера будем понимать медленное снижение оценки данного примера по отношению к снижению оценки по обучающему множеству. Для того чтобы ускорить обучение данного примера, ему можно приписать вес, больший, чем у остальных примеров. В случае, когда количества примеров в разных классах сильно различаются, следует увеличить веса всем примерам того класса, в котором их меньше. Опыт показывает, что использование весов в таких ситуациях позволяет улучшить обобщающие способности сети.

Третья ситуация – различная достоверность разных примеров – то же может решаться таким способом. Для этого менее достоверным примерам задают меньшие вес. Однако правильным является другой подход. Низкая достоверность ответа означает, что эксперт, выдавший этот ответ, сомневается в его правильности. Для получения хорошей экспертной системы следует добиться того, чтобы нейронная сеть в этом случае также «сомневалась» в правильности ответа. Под сомнением сети понимается более низкий уровень уверенности. Эта цель достигается, уменьшением уровня надежности при вычислении оценки сомнительного примера. Причем чем сильнее сомневался эксперт, тем меньший уровень надежности используется для данного примера.

Для достижения наилучшего эффекта можно использовать комбинацию этих методов. В этом случае оценка и градиент оценки вычисляются по следующим формулам:

где 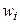– вес примера, – его достоверность.

Глобальные и локальные оценки.

Определение. Локальной называется любая оценка, являющаяся линейной комбинацией произвольных непрерывно дифференцируемых функций, каждая из которых зависит от оценки только одного примера.

Использование локальных оценок позволяет обучать сеть решению как отдельно взятого примера, так и всего обучающего множества в целом. Однако существуют задачи, для которых невозможно построить локальную оценку. Более того, для некоторых задач нельзя построить даже обучающее множество.

Составные интерпретатор ответа и оценка. Поскольку сеть может решать сразу несколько подзадач (выдавать несколько ответов), то интерпретатор ответа и оценка являются составными: на каждый ответ своя оценка и свой интерпретатор ответа. Нет никаких ограничений на типы используемых интерпретаторов или оценок. Оценка примера в целом получается путем суммирования оценок отдельных подзадач.

Если важность правильного ответа на разные подзадачи различна, при построении оценки примера можно задействовать механизм весов задач. Тогда оценка примера будет являться линейной комбинацией оценок отдельных подзадач с весами подзадач в качестве коэффициентов.

Исполнитель. Компонент исполнитель является служебным. Это означает, что он универсален и невидим для пользователя. В отличие от всех других компонентов исполнитель не выполняет ни одной явной функции в обучении нейронных сетей, а является вспомогательным для компонентов учитель и контрастер. Задача этого компонента – упростить работу компонентов учитель и контрастер. Этот компонент выполняет всего два запроса, преобразуя каждый из них в последовательность запросов к различным компонентам.

Учитель. Этот компонент не является столь универсальным как задачник, оценка или нейронная сеть, поскольку существует ряд алгоритмов обучения жестко привязанных к архитектуре нейронной сети. Примерами таких алгоритмов могут служить обучение (формирование синаптической карты) сети Хопфилда, обучение сети Кохонена и ряд других аналогичных сетей. Однако существует способ формирования сетей, позволяющий обучать сети Хопфилда и Кохонена методом обратного распространения ошибки. Описываемые методы обучения ориентированы в первую очередь на обучение двойственных сетей (сетей обратного распространения ошибки).