ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ.

Элементы теории графов

Введение.История возникновения теории графов

 

Почти каждый в своё время рисовал кружочки и соединял их линиями, пытался нарисовать небольшую карту, генеалогическое дерево. Либо ломал голову над тем, как соединить несколько точек, не проводя одну и ту же линию дважды.

Исторически сложилось так, что теория графов зародилась именно в ходе решения головоломок двести с лишним лет назад. Начало теории графов относят к 1736г., когда Л.Эйлер не только решил популярную в то время задачу о кенигсбергских мостах, но и нашёл критерий существования в графе специального маршрута (эйлерова цикла, как теперь его называют). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Г. Кирхгоф разработал теорию деревьев для исследования электрических цепей, а английский математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для некоторых типов деревьев. К этому же периоду относится появление знаменитой проблемы четырёх красок.

Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кёнига в 30-е годы XX столетия.

В последнее время графы и связанные с ними методы исследованийорганически пронизывают на разных уровнях едва ли не всю современную математику. Графы эффективно используются в информатике, теории планирования и управления, теории расписаний, социологии, экономике, биологии, медицине. Широкое применение находят графы втаких областях прикладной математики, как теория конечных автоматов, электроника, теория вероятностей, комбинаторика.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ.

Задача 1.1. Давайте решим несложную задачу. Лист бумаги Плюшкин, герой романа ²Мертвые души², разрезает на три части. Некоторые из полученных листов он также разрезает на три части. Несколько новых листиков он вновь разрезает на три более мелкие и т. д. Сколько Плюшкин получает листиков бумаги, если разрезает k листов?

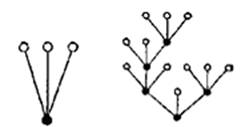
рис. 1.1 рис. 1.2

 

Решение. Листы бумаги обозначим на рисунке кружками. Кружки, соответствующие листам, которые разрезаются, закра­сим целиком; остальные кружки оставим незакрашенными.

Рисунок 1.1 позволяет увидеть, что при разрезании одного лист­ка на три части число листков увеличивается на два (появляются три новых вместо одного: 3 = 1 + 2×1). Если же было разрезано k листов, то образовалось 1 + 2 k листов (рис. 1.2).

На рисунке 1.2 показано пять разрезаний. Сколько в этом слу­чае получено листов?

Стоит заметить, что схемы на рисунках 1.1 и 1.2 напо­минают ветку дерева с листочками, поэтому математики и назвали такие схемы «деревьями».

Что же общего у схем, которые помогли нам в решении задачи? Все они состоят из точек (кружков) и отрезков, соединяющих пары точек. Схемы железных или шоссейных дорог, структурные формулы молекул, либо всё что показывает только связи между объектами, являются примерами графов. Рассмотрение таких схем и приводит к понятию графа. Деревья -частный вид графов.

Термин «граф» впервые появился в книге венгерского математика Д.Кёнига в 1936 г. Графом G называется упорядоченная пара множеств G =(V,E), где V- непустое конечное множество элементов (вершин графа), а E - множество неупорядоченных их пар (рёбер графа). Вершины графа на рисунках выделяют обычно кружками или квадратиками потому, что не всегда точки пересечения ребер принимаются за вершины графа. Например, граф на рисунке 1.3 имеет 4 вершины и 6 ребёр:

 

Рис. 1.3

но точка пересечения «диагоналей четырехугольника» вершиной не является.

При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны. Все три фигуры на рисунке 1.4 изображают один и тот же граф.

 

 

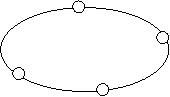Рис. 1.4

 

На рисунке 1.5 изображён граф с четырьмя вершинами и 1 ребром.

На рисунке 1.6 изображён граф с шестью вершинами, не имеющий ни одного ребра.

 

Рис. 1.5 рис. 1.6

 

Вершины, не принадлежащие ни одному ребру, называются изолированными.

Граф на рисунке 1.6 имеет две изолированные вершины, а в графе, изображенном на рисунке 1.7, все шесть вершин изолированные.

Число вершин графа G называется его порядком и обозначается через |G|. Если |G| = n, а число ребер равно m, то G называют (n,m)-графом.

Граф порядка n, у которого нет рёбер, называется пустым и обозначается О_n. На рисунке 1.6 показан пустой граф О₆. Часто обозначают вершины графа обычно заглавными буквами русского или латинского алфавитов (А, В.....L, S,…), иногда числами. В этом случае граф называется помеченным. Рёбра графа обозначаются парами вершин, например (A, B) или (1, 5), либо малыми буквами русского или латинского алфавитов.

Если сущёствует ребро (A, B), то вершины А и В называются смежными. На рисунке 1.7 вершины Т и М смежные, а вершины А и М не являются смежными.

Граф называется полным, если любые две его вершины смежны. (рис. 1.8). В полном графе порядка n у каждой вершины одинаковое количество (n-1) рёбер. Для задания полного графа достаточно знать его порядок. Полный граф порядка n обозначается символом Kn, число рёбер в нём равно n(n-1)/2.

А Л

 

 

Т М

 

Рис. 1.7 рис 1.8

Граф не являющийся полным, можно преобразовать в полный, добавив недостающие ребра. Например, граф G на рисунке 1.9 неполный. Проведя недостающие ребра, получаем полный граф порядка 4 (рис. 1.10).

Вершины графа G и ребра, которые добавлены, тоже образуют граф. Он показан на рисунке 1.11. Такой граф называют дополнением графа G и обозначают его G'.

Дополнением графа G называется граф G’ с теми же вершинами, что и граф G, и с теми и только теми ребрами, которые необходимо добавить к графу G, чтобы получился полный граф.

 

Рис 1.9 рис 1.10 рис. 1.11

 

Определение:граф G = <V, E> называется изоморфным графу H = <V1, E1>, если существует взаимнооднозначное отображение φ множества V вершин графа G на множество вершин V1 графа H, при котором сохраняется смежность соответствующих вершин.

 

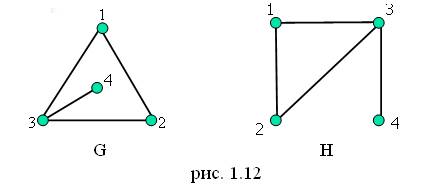
На рисунке 1.12 изображены два изоморфных графа порядка 4.

Числовые характеристики, сохраняющиеся при изоморфизме, называются инвариантами графа. Число вершин и ребер графа, количество ребер у вершины являются инвариантами графа.

Пример: Построить 11 неизоморфных графов порядка 4 (рис1.13).

 

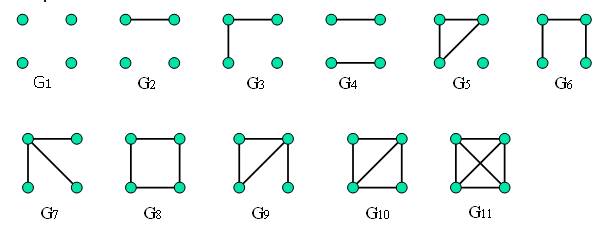
Рис 1.13

Граф G₁ - пустой О₄. Граф G₂ имеет одно ребро и потому не изоморфен графу G₁. Графы G₃ и G₄ имеют по 2 ребра, но у G₃ есть изолированная вершина, чего нет у G₄, поэтому они не изоморфны между собой и предыдущим графам. Аналогично доказывается, что графы G₅ - G₁₁ попарно не изоморфны и не изоморфны графам G₁ - G₄.

Пойа нашёл приближённую формулу вычисления числа q_n не изоморфных графов порядка n (при малых n она не эффективна):

.

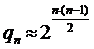ОБОБЩЕНИЯ ПОНЯТИЯ ГРАФА

 

Иногда приведенное выше определение графа оказывается недостаточным и приходится рассматривать более общие объекты, состоящие из двух конечных множеств.

Определение: пара множеств G = <V,E> называется ориентированным графом (орграфом), если V – конечное, непустое множество вершин, а Е – множество упорядоченных пар (A, B) элементов из V. Ориентированное ребро (A, B) будем называть дугой с началом A и концом B. На рисунке дуги изображаются стрелками (рис 2.1).

Определение: пара множеств G = <V,E>, где V – конечное, непустое множество вершин, а Е содержит «параллельные» рёбра (т.е. вершины могут соединяться более чем одним ребром) называется мультиграфом (рис. 2.2).

Определение: пара множеств G = <V,E>, где V – конечное, непустое множество вершин, а Е – множество ребер, содержащее ²петли², т.е. ребра, соединяющие вершину саму с собой, называется псевдографом (рис. 2.3).

Псевдограф на рис. 2.3 содержит 2 петли e₁ и e₂.

Определение: пара множеств G = <V,E>, где V – конечное, непустое множество вершин, а Е – множество ²рёбер², состоящих из произвольных подмножеств множества V, называется гиперграфом (рис. 2.4).

На рисунке 2.4 изображен гиперграф с тремя ²ребрами²: e₁= (1,2), e₂= (3,4) и e₃= (4, 5, 6).

 

§ 3. ПРЕДСТАВЛЕНИЕ ГРАФОВ В ПАМЯТИ КОМПЬЮТЕРА

 

Естественный способ представления графа рисунком на плоскости в виде точек и соединяющих их линий не годится, если мы хотим решать с помощью ЭВМ задачи, связанные с графами. Выбор соответствующей структуры данных для представления графов имеет принципиальное влияние на эффективность алгоритмов работы с графами, поэтому рассмотрим несколько различных способов представления ориентированных и неориентированных графов и отметим их достоинства и недостатки.

В теории графов классическим способом представления помеченного графа порядка n служит матрица смежности А = (a_ij) размера n´n, где a_ij =1, если существует ребро (i,j) и a_ij =0 в противном случае (рис. 3.1)

Аналогично определяется матрица смежности для ориентированного графа:

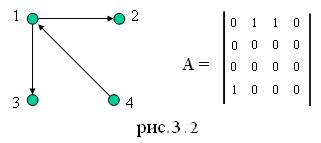
Матрица смежности графа симметрична относительно главной диагонали (для орграфа это свойство матрицы обычно не выполняется).

Основным преимуществом представления графа матрицей смежности является тот факт, что за один шаг можно получить ответ на вопрос: Не ²существует ли ребро из i в j?². Недостатком же является тот факт, что независимо от числа ребер объем занятой памяти составляет n² ячеек, что в настоящее время совершенно неважно.

Более экономным в отношении памяти (в случае m £ n²) является представление графа списком ребер - массивом B пар вершин, соответствующих его ребрам (рис. 3.3).

Очевидно, объем памяти в этом случае составляет 2m ячеек. Недостатком является большое число шагов - порядка m в худшем случае - необходимое для получения ответа на вопрос, существует ли ребро (i,j).

Лучшим решением во многих случаях оказывается структура данных, которая называется списками смежностей - массив динамических списков вершин смежных для каждой вершины графа (рис.3.4).

Для неориентированных графов каждое ребро (i,j) представлено дважды: через вершину j в списке со ссылкой i и через вершину i в списке со ссылкой j.