А)Аэродинамические св-ва пылевых частиц. б) Аэродинамическая сила. в) коэф-т сопротивления. г) скорость витания.

а) Поток частич подобно струйному нагнетателю способен сформировать направленное течение в/х.

Явление увлечения в/х потоком твердых частиц называется – эжекцией. Структура эжекционных потоков их геометрия скоростные параметры во многом определяют методологию расчета и конструирования обеспыливающих систем.

в) Коэф-т лобового сопротивления падающей частицы.

Проинтегрируем ур-ние динамики

Sβ₁V₁ρ₁dv₁₌ Sβ₁V₁ρ₁gdx- R*n_1* S *dx (1)

Sβ₂V₂ρ₂dv₂₌S β₂(ρ₂-ρ₀)gdx- S β₂dp- * β₂S+R*n_1* S *dx (2)

При загрузке герметичного бункера сыпучим не нагретым материалом по вертикальному желобу. При этом ур-ние (2) упрощается по следующим причинам

1-скорость эжектируемого в/х в потоке V₂=0 4- сила аэродинамического сопротивления

2-ρ₂₌ρ₀одной частицы

3- β₂₌₁

5- Число падающих частиц в единицу объема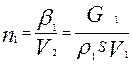

6- S=const

C с учетом этого перепишем ур-ние (1)и(2)

V₁d V₁= dx (3) (4)

Проинтегрируем (2)имея ввиду что

P’-P_атм (5)

Отсюда видно что в желобе возникает избыточное давление увеличивающееся на пути падения частицы.

При небольших высотах падения достаточно больших частиц вес которых намного больше силы аэродинамического сопротивления

ρ₁V_чg>>R bp (1) имеем

V₁d V₁₌gdx или dx= V₁d V_1/g

P’-P_атм= (6)

Тоесть избыточное давление в желобе изменяется от (x=0 V_1н=V_1к)

V₁d V₁₌gdx= (7)

ΔP_max= (8)

Таким образом измерив избыточное давление в конце желоба можем при известном расходе найти лобовое сопротивления падающей частицы

(9)

Этот способ предложен Логачевым И. Н. он имеет следующие достоинства

1- невмешательство в процесс впадения

2- использование простейших приборов

В результате выполненных экспериментальных иследованний была получена следующая эмперическоя фор-ла для определения коэф –та лобового сопротивления

Частицы в потоке

(10)

ψ₀- Коэф-т аэродинамического сопротивления одиночной частицы в области автомодельности.

d_э- Эквивалентный диаметр частицы

= (11)

Из (10) видно что коэф-т сопротивления частицы в потоке меньше коэф-та сопротивления

Одиночной частицы связанно это с тем что, увеличение концентрации пыли и

Проявляется взаимное влияние частиц на режим обтекания (влияние аэродинамической тени).

Таким образом аэродинамическое сопротивление падающих частиц зависит то диаметра частицы ее формы числа Re и от концентрации частиц в потоке.

г) Скорость падения частиц в не подвижном в/хописывается следующим диф-ур

m= dv/dt=mg-R

При росте скорости падения увеличивается и сопротивление среды (R) и в какой-то момент настает условие когда сила веса уравновешивается сило аэродинамического сопротивления среды, наступает режим равномерного падения (mg=R), наступает процесс седиментации (равномерного осаждения, частица падает с равномерной скоростью).

Скорость равномерного падения частицы называется седиментационной скоростью которая численно ровна скорости витания.

Скорость витания – это скорость восходящего воздушного потока при котором частица витает (не меняет своего горизонтального положения.

Для пылевых частиц R=3πμd_эv (R<1) ламинарное обтекание