1. Для равновесия твердого тела или системы тел необходимо одновременное выполнение двух условий:
Твердым телом называется тело, расстояние между любыми двумя точками которого не изменяется с течением времени (или меняется пренебрежимо мало).
I 
условие равновесия: Сумма внешних сил, действующих на систему, должна быть равна нулю.
Внешними называются силы, действующие на тела, входящие
в систему, со стороны тел, не входящих в эту систему.
II 
условие равновесия: Сумма моментов внешних сил, действующих на систему,
должна быть равна нулю относительно любой оси вращения.
2. 
|
|
|
r Знак «+» берется, если сила F стремится повернуть тело
|
знак « - » — если по часовой. F
Единица измерения М в СИ: 1 Н×м
из оси вращения на линию действия этой силы
Замечание.
|
r
F плоскости перпендикулярной оси вращения.
|
3. Не всегда одновременное выполнение I и II условий равновесия гарантирует неподвижность механической системы. Покой системы невозможен в положениях неустойчивого равновесия (т.е. в таких положениях, любое бесконечно малое смещение из которых, приво- дит к тому, что сумма внешних сил (или их моментов) стремится еще больше удалить систему от равновесного положения). Реализованы могут быть только положения устойчивого равновесия (т.е. такие положения, любое бесконечно малое смещение из которых, приводит к тому, что сумма внешних сил (или их моментов) стремится вернуть систему обратно в равновесное положение) и положения безразлич- ного равновесия (т.е. положения, при бесконечно малых смещениях из которых сумма внешних сил и их моментов остается равна нулю).
4. 
Центром масс системы материальных точек m 1, m 2, …, mN называется геометрическая точка (С), координаты которой определяются формулами:
Центр тяжести (т. е. точка приложения равнодействующей силы тяжести) совпадает с центром масс системы, если эта
система находится в однородном гравитационном поле (или напряженность поля тяготения меняется в пределах системы
незначительно)
(т.е. жидкость неподвижная относительно стенок сосуда)
5. 
Сила гидростатического давления — сила, с которой покоящаяся жидкость действует на погруженные в нее тела, стенки и дно сосуда, в котором жидкость находится (без учета поверхностного
По своей природе эта сила
является
силой объемной упругости Она возникает, если жидкость
натяжения).
|
6. Давлением жидкости на плоскую поверхность называется отношение силы гидростатического давления, действующей на эту поверхность, к площади поверхности (при условии, что сила распределена по поверхности равномерно).
|
|
Сила гидростатического давления, действующая
dF
p = гидр. давл.
dS
Единица измерения давления в СИ: 1Па = 1 Н/м2.
на бесконечно малую площадку dS
площадь бесконечно малой площадки
(эта площадь dS мала на столько, что площадку можно с достаточной точностью считать плоской и
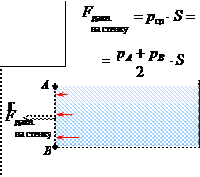изменением давления в пределах dS можно пренебречь)
7. Давление в какой-либо точке жидкости — это давление на воображаемую
бесконечно малую площадку, на которой лежит эта точка. Причем, можно доказать, что
 |
давление в данной точке жидкости не зависит от ориентации той воображаемой бесконечно малой площадки, на которую производится это давление.
Док-во: Мысленно выделим в жидкости прямоугольный параллелепипед А 1 В 1 С 1 D 1 А 2 В 2 С 2 D 2. Площадь А 1 В 1 С 1 D 1 так мала, что во всех ее точках давление одинаково. Сторона А 1 А 2 горизон- тальна. Выделенный объем жидкости находится в равновесии, поэтому сумма всех действующих
r С 1
F 1 В 1
С 2 r
В 2 F 2
D
r r r r r
А 1 D 1
А 2 2
на него сил равна нулю: mg + F 1 + F 2 + F бок = 0 (Сила F бок — сумма сил mg
гидростатического давления на боковые поверхности А 1 В 1 В 2 А 2, В 1 С 1 С 2 В 2, С 1 D 1 D 2 C 2, D 1 A 1 A 2 D 2.) О
В проекциях на горизонтальную ось ОХ это уравнение имеет вид: F 1 – F 2 = 0 Þ F 1 = F 2 Разделив обе части этот равенства на площадь Х
|
9. 
В однородной покоящейся жидкости давления в точках, лежащих на разных
r - плотность жидкости
горизонтальных уровнях, отличаются на
давление в точке, лежащей
p н - p в = r gh
h - расстояние между верхним
и нижним уровнями
на более низком уровне давление в точке,
лежащей на более высоком уровне
g - ускорение свободного падения
r
F в Y
Док-во: Мысленно выделим в жидкости прямоугольный параллелепипед с горизонтальными основаниями.
Выделенный объем жидкости находится в равновесии, поэтому сумма всех действующих на него сил равна нулю:
r r r r r
mg + F н + F в + F бок = 0 (Сила F бок
— сумма сил гидростатического давления
на боковые вертикальные поверхности.) h
В проекциях на вертикальную ось ОY это уравнение имеет вид: – mg + F н – F в = 0 Þ F н – F в = mg = r Shg
(здесь масса выделенного объема жидкости m представлена как произведение ее плотности r на объем V = Sh
Разделив обе части этот равенства на площадь основания S, получим: p н - p в = r gh.
10. Архимедова сила — выталкивающая (подъемная) сила, действующая на тело, погруженное
r
F н О
r r r
в жидкость или газ. Архимедова сила есть сумма всех сил гидростатического давления,
Рис. 10.1
F Арх = F 1 + F 2 +
|
действующих на тело, погруженное в жидкость или газ (кроме тех случаев, когда тело плотно прижато к дну или стенке сосуда так, что жидкость (газ) не проникает между телом и дном (стенкой) — в этих случаях суммарную силу гидростатического давления не называют архимедовой силой)
r
|
|
Vпогр
1 r r
F = m × g ускорение свободного
|
F АРХ = rж× V погр× g
если жидкость
F 2 r
F 3
r F 5
F 4
m выт — масса «вытесненной» жидкости — масса такой
же жидкости, как вокруг тела, которая уместилась бы в объеме погруженной части тела V погр
однородна
r — плотность среды (жидкости или газа), в которую погружено тело
r r r r
Док-во: Сумма сил гидростатического давления F 1 + F 2 +K+ FN = F Арх, действующих на объем V погр не зависит от того, какое вещество
r r
r
F Арх
находится внутри этого объема (F 1, F 2, … – силы упругости, они зависят от деформации жидкости, окружающей объем
V погр, а не от содержимого этого объема). Мысленно выделим в покоящейся жидкости объем, совпадающий с V погр по форме и расположению (рисунок 10.2). На него будут действовать точно такие же силы гидростатического давления
Рис. 10.2 r r
F 1, F 2, …, как и на объем погруженной части тела V погр. Выделенный в жидкости объем находится в равновесии, значит,
r r
F Арх + m выт g = 0
r
Þ F АРХ = m выт× g, что и требовалось доказать.
r FN
(В этом доказательстве считается, что атмосферного давления нет. Чтобы учесть его наличие, можно
рассматривать тело на рисунке 10.1, как плавающее на границе раздела двух сред – жидкости (r2) и воздуха (r1))
|
r F 5
F 2 r
F 3 F 4
Если тело плавает на границе нескольких сред, плотностями r1, r2, … (На рис. 10.3 пример, когда сред две), то масса вытесненной жидкости m выт находится как сумма m выт = r1 V 1 + r2 V 2 + …
Рис. 10.3
|
(V 1 — объем той части тела, которая погружена в первую среду,
V 2 — объем той части тела, которая погружена во вторую среду, и. т. д.)
r
11. Если сосуд с жидкостью движется с ускорением a в ИСО, то в системе отсчета, связанной с сосудом, на каждую
r
r2 V 2
|
относительно сосуда, то в системе отсчета, связанной с движущимся сосудом, можно использовать формулы из r
пунктов 9 и 10, заменяя в них g r на
g ¢= g r - a r.
g r¢
F Арх
= -r V погр
g r¢
p 2 = p 3 h
p 1 – p 2 = r g ¢ h
2 g
a
1 3 - a r
V. 
Тепловые явления
1. Уравнение Менделеева-Клапейрона
Давление газа (в Па) 1 атм » 105 Па » 760 мм.рт.ст.
Объем газа (в м3)
|