| определение | отношение сравнения | сложение | умножение | вычитание | деление | |
| Теоретико – множественный смысл натурального числа и нуля | Натуральное число – это общее свойство класса конечных равномощных множеств. Число 0 – это свойство класса пустых множеств. | Число а равно числу b, где а = n(А) и b = n(В), если множество А равномощно множеству В. а = b Û А ~ В (n (А)= n (В)), при n (А)= а, n (В)= b Число а меньше (больше) числа b, где а = n (А) и b = n (В), если во множестве В можно выделить собственное подмножество В1 равномощное множеству А. a < b, а = n(А) и b = n(В) Û $В1, В1Ì B, В1 ~ А, В1 ¹ B, В1 ¹ Æ. a > b, а = n(А) и b = n(В) Û $А1, А1 Ì А, А1 ~ B, А1 ¹ А, А1 ¹ Æ. | Сумма чисел а и b представляет собой число элементов в объединении конечных непересекающихся множеств А и В, таких, что а = n (А) и b = n (В). а + b = n (А) + n (В) = = n(А È В),если АÇВ=Æ | Произведение чисел а и b представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются. а · b = n(А1È А2È…ÈАb), если n(А1)=n(А2)=...= n(Аb) и А1, А2,… Аb попарно не пересекаются. Произведение чисел а и b представляет собой число элементов в декартовом произведении множеств А и В таких, что а = n(А) и b = n(В). а ·b = n(А) · n(В) = n(А´В) | Разность чисел а и b представляет собой число элементов в дополнении множества В до множества А, при а = n(А) и b = n(В) и В Ì А. а - b= n(А - n(В) =n(А\В), если В Ì А. | Частное чисел а и b представляет собой 1)число элементов каждого из равномощных попарно не пересекающихся классов разбиения множества А 2) число равномощных попарно не пересекающихся классов разбиения множества А таких, что а = n(А) и b = n(Аi), А1, А2,… Аn Ì А, n – количество классов разбиения. 1) а: n = bделение на равные части; 2) a: b = nделение по содержанию. |
| Аксиоматическое построение системы натуральных чисел | Множество N, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам: 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества (единица 1); 2. Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а; 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует элемента а; 4. Всякое подмножество М множества N, обладающее свойствами 1 Î М и из того, что а Î М, следует, что и а' Î М, совпадает с множеством N; называется множеством натуральных чисел, а его элементы – натуральными числами. | Число а меньше (больше) числа b (a < b, a > b) тогда итолько тогда, когда существует такое натуральное число с, что а + с = b (b + c=a). a < bÛ $ сÎN, а+ с = b | Сложением натуральных чисел называется алгебраическая операция, обладающая свойствами: 1." аÎ N, а + 1 = а', 2." а,bÎ N, а +b' =(a +b)' Свойства: 1)" а,bÎN, $!сÎN, c=a+b; 2)"а,bÎN,(a+b)+c=a+(b+c); 3)"а bÎN, a + b= b + a; 4))"а bÎN, a + b ¹ b. | Умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 1. " аÎ N, а · 1 = а, 2." а,b Î N, а ·b' =a · b+ a. Свойства: 1)" а,bÎN, $!сÎN, c=a ·b; 2)"а,b,сÎN,(a+b)·c=a·с+b·c 3)"а,b,сÎN,c·(a+b)=c·a+c·b 4)"а,b,сÎN,(a·b)·c=a·(b·с); 5))"а,bÎN, a·b=b·a. | Вычитанием натуральных чисел а и b называется алгебраическая операция, удовлетворяющая условию а – b = с тогда и только тогда, когда b + с = а. а – b = с Û b + с = а. Свойства: 1)" а,bÎN, $cÎN, c=a–bÛ a > b; 2) " а,bÎN, $cÎN, c=a–bÞ !c, c=a–b; 3)"а,b,сÎN, a) a >c, (a+b)–c = (a–с)+ b; б) b>c, (a+b)–c =a + (b–с); 4)"а,b,сÎN, a–(b+c) = (a–b)–c = (a–c)–b. | Делением натуральных чисел а и b называется алгебраическая операция,
удовлетворяющая условию а: b = с тогда и только тогда, когда b· с = а.
а: b = с Û b· с = а.
Свойства:
1)" а,bÎN, $cÎN, c=a:bÞ
a ³ b;
2) " а,bÎN, $сÎN, c=a:bÞ
!c, c=a:b;
3)"а,b,сÎN,
a 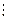 с и b с и b  с Þ (a + b) с Þ (a + b)  c;
4)"а,b,сÎN, a > b,
a c;
4)"а,b,сÎN, a > b,
a 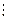 с и b с и b  с Þ (a– b) с Þ (a– b)  c;
5)"а,b,сÎN,
a c;
5)"а,b,сÎN,
a 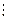 с или b с или b  с Þ (a·b) с Þ (a·b)  c;
6) Ø$c, с = а: 0;
7)" а,bÎN, $!(q; r), q; rÎN,
a = b·q + r, 0 £ r <b. c;
6) Ø$c, с = а: 0;
7)" а,bÎN, $!(q; r), q; rÎN,
a = b·q + r, 0 £ r <b.
|
| Натуральное число как мера величины | Натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. Х = а · Е или а = mЕ (Х) | Натуральное число а, являющееся мерой длины отрезка х, меньше (больше) натурального числа b, являющегося мерой длины отрезка у, если отрезок х короче (длиннее) отрезка у. a < b Û х < y a > b Û x > y, если а=mЕ (Х), b=mЕ (Y) | Сумму натуральных чисел а и b можно рассматривать как меру длины отрезка х, состоящего из отрезков y и z, мерами которых являются числа а и b. a + b = mЕ (Y) + mЕ (Z) = = mЕ (Y + Z) = mЕ (Х) | Если натуральное число а – мера длины отрезка х при единице длины Е, натуральное число b – мера длины Е при единице длины Е1, то произведение а ·b – это мера длины отрезка х при единице длины Е1. а· b =mЕ (Х) · mЕֽ (Е)=mЕֽ (Х) | Разность натуральных чисел а и b можно рассматривать как меру длины такого отрезка z = х q у, что z Å y = x, если мера длины отрезка х равна а, мера длины отрезка у равна b. a - b = mЕ (Х) - mЕ (Y) = = mЕ (X -Y) = mЕ (Z) | Если натуральное число а – мера длины отрезка х при единице длины Е, натуральное число b – мера длины Е1 при единице длины Е, то частное а: b – это мера длины отрезка х при единице длины Е1. а:b=mЕ (Х):mЕ (Е1)=mЕֽ (Х) |
| Запись натуральных чисел и алгоритмы действий с ними | Десятичной записью натурального числа х называется его представление в виде х = аn· 10n + аn-1· 10n-1+ + … + а1· 10 + a0· 100,где коэффициенты аn, аn-1, …, а1, a0принимают значения 0,1,2,3,4,5,6,7,8,9 и аn¹0. | Пусть натуральные числа х и у таковы, что х = аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100 и у = bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 . тогда число х меньше числа у, если выполнено одно из условий: 1) n < m; 2) n = m, но an < bn; 3) n = m, an = bn, …, ak = bk, но ak-1 < bk-1. | Пусть натуральные числа х и у таковы, что х = аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100 и у = bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 . если n > m; х + у = аn· 10n +…+ (аm·10m + bm·10m ) + … + (а1· 10 + b1· 10) + (a0 + b0 ) = аn· 10n + … + (аm + bm ) ·10m +… + (а1 + b1 ) · 10 + (a0 + b0 )·100 | Пусть натуральные числа х и у таковы, что х = аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100 и у = bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 . если n > m х· у = аn· bm·10n+m + … + аn· b0· 10n + … + a0· b0· 100 | Пусть натуральные числа х и у таковы, что х = аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100 и у = bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 . если n > m х – у = аn· 10n + … + + (аm– bm) ·10m + … + (а1 –b1) · 101 +(a0 – b0 ) · 100 | Пусть натуральные числа х и у таковы, что х = аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100 и у = bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 . если n < m Ø$cÎN, с=х: у если n = m х: у = с· 100, с· у = х; если n > m х: у = (аn· 10n + аn-1· 10n-1+ +… + а1· 10 + a0· 100): : (bm·10m + bm-1· 10m-1+ + … + b1· 10 + b0· 100 ) = 1) (аn· 10n + аn-1· 10n-1+ … + + аn-m· 10n-m ): (bm·10m + + bm-1· 10m-1+ … + b1· 10 + b0· 100 ) = q1; 2) (аn· 10n + аn-1· 10n-1+… + а1· 10 + a0· 100) – (bm·10m + bm-1· 10m-1+ … + b1· 10 + b0· 100) ·q1= r1; 3) r1·10n-m + аn-m-1· 10n-m-1 +…+а1· 10 +a0·100): (bm·10m + bm-1·10m-1+ … + b1· 10 + b0· 100 ) = q2; 4)… 5)rk·10k +…+а1· 10+a0· 100): : (bm·10m + bm-1·10m-1+ … + + b1· 10 + b0· 100 ) = qk; 6) х: у = q1q2…qk |
Свойства бинарных отношений
| Название | Определение | Вид графа | Пример |
| Рефлексивность | Отношение Р, заданное на множестве М, называется рефлексивным, если каждый элемент этого множества связан сам с собой этим отношением. Р рефлексивно Û "аÎМ, аРа |
 Около каждой точки графа есть петля:
·
· ·
· Около каждой точки графа есть петля:
·
· ·
·
| Р: «число х равно числу у » на множестве чисел. «" х, х = х »– верно, следовательно отношение «быть равными» рефлексивно. |
 Антирефлексивность
Антирефлексивность
|
Отношение Р, заданное на множестве М, называется антирефлексивным, если ни один элемент этого множества не связан сам с собой этим отношением.
Р антирефлексивно Û "аÎМ, 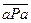
| Нет ни одной точки с петлей: · · · · | Р: «человек х выше человека у » на множестве людей. «" х, человек х выше человека х »– не верно, рефлексивность не выполняется; «" х, человек х не выше человека х » – верно, следовательно отношение «быть выше» антирефлексивно. |
 Симметричность
Симметричность
| Отношение Р, заданное на множестве М, называется симметричным, если для любых двух элементов этого множества, из того, что первый элемент связан со вторым, следует, что и второй связан с первым. Р симметричноÛ ("а, bÎМ, аРb Þ bРа) | Каждой стрелке графа есть обратная (все стрелки графа двойные): · · · · | Р: «слово х имеет тот же корень, что и слово у » на множестве слов. «" х,у; если слово х имеет тот же корень, что и слово у, то слово у имеет тот же корень, что и слово х » – верно, следовательно отношение «иметь один и тот же корень» симметрично. |
 Антисимметричность
Антисимметричность
|
Отношение Р, заданное на множестве М, называется антисимметричным, если для любых двух элементов этого множества, из того, что первый элемент связан со вторым, следует, что второй не связан с первым.
Р антисимметрично Û
("а,bÎМ, а¹b и аРb Þ  ) )
| Нет ни одной обратной стрелки (все стрелки графа одинарные): · · · · | Р: «арбуз х тяжелее арбуза у » на множестве арбузов. «" х,у; если арбуз х тяжелее арбуза у, то арбуз у нетяжелее арбуза х » – верно (т.к. арбуз у легче арбуза х), следовательно отношение «быть тяжелее» антисимметрично. |
| Транзитивность | Отношение Р, заданное на множестве М, называется транзитивным, если для любых трех элементов этого множества, из того, что первый элемент связан со вторым, а второй связан с третьим, следует, что первый связан с третьим. Р транзитивно Û ("а,b,сÎМ, аРb и bРс Þ аРс) | Для любых трех точек графа выполняется «правило треугольника» (правило сложения векторов по правилу треугольника): · · · · | Р: «город х находится восточнее города у » на множестве городов России. «" х,у,z; если город х находится восточнее города у и город у находится восточнее города z, то город х находится восточнее города z» - верно, следовательно отношение «находиться восточнее» транзитивно. |
 Антитранзитивность
Антитранзитивность
|
Отношение Р, заданное на множестве М, называется антитранзитивным, если для любых трех элементов этого множества, из того, что первый элемент связан со вторым, а второй связан с третьим, следует, что первый не связан с третьим.
Р антитранзитивно Û
("а,b,сÎМ, аРb и bРс Þ 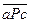 ) )
| Для любых трех точек графа, если есть три последовательно связанных элемента, то нет связи между первым и третьим элементом: · · · · | Р: «прямая х перпендикулярна прямой у » на множестве прямых плоскости. «" х,у,z; если прямая х перпендикулярна прямой у и прямая у перпендикулярна прямой z, то прямая х не перпендикулярна прямой z » - верно (прямые х и z параллельны), следовательно отношение «быть перпендикулярным» антитранзитивно. |
  Связанность
Связанность
| Отношение Р, заданное на множестве М, называется связанным, если любые два не равные между собой элемента связаны между собой. Р связанноÛ ("а,bÎМ, а¹b, аРb или bРа) | Все точки графа связаны между собой стрелкой (одинарной или двойной): · · · · | Р: «число х больше числа у» на множестве чисел. «" х,у; при х ¹ у, верно х > у или у > х » - верно, следовательно отношение «быть больше» является связанным. |