СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

1. Задачи науки о сопротивлении материалов.

Сопромат – это наука о прочности, жесткости и устойчивости инженерной конструкции.

Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений.

Задачей сопротивления материалов, как одного из разделов механики, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.

Жесткость – способность элемента конструкции сопротивляться упругим деформациям.

Прочность – способность конструкции выдерживать заданную нагрузку не разрушаясь.

Устойчивость – способность элементов конструкции сохранять прямолинейную форму упругого равновесия.

2. Классификация объектов расчета и нагрузок: статистическая нагрузка, динамическая нагрузка, сосредоточенная нагрузка, распределенная нагрузка.

Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.

По способу приложения:

Сосредоточенные нагрузки передают свое действие через,очень малые площади. Примерами таких нагрузок могут служить давление колес железнодорожного вагона на рельсы, давление тележки тали на монорельс и т. д.

Распределенные нагрузки действуют на сравнительно большой площади. Например, вес станка передается через станину на всю площадь соприкосновения с фундаментом.

По продолжительности действия принято различать постоянные и переменные нагрузки. Примером постоянной нагрузки может служить давление подшипника скольжения — опоры валов и осей — и его собственный вес на кронштейн.

Переменной нагрузке подвержены в основном детали механизмов периодического действия. Одним из таких механизмов служит зубчатая передача, у которой зубья в зоне контакта смежных пар зубчатых колес испытывают переменную нагрузку.

По характеру действия нагрузки могут быть статическими и динамическими. Статические нагрузки почти не изменяются в течение всего времени работы конструкции (например, давление ферм на опоры).

Динамические нагрузки действуют непродолжительное время. Их возникновение связано в большинстве случаев с наличием значительных ускорений и сил инерции.

Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механизмов также испытывают во время работы значительные динамические нагрузки от изменения величины и направления скоростей, то есть наличия ускорений.

Циклические нагрузки - многократно изменяющиеся во какому нибудь периодическому закону.

3. Деформация. Гипотезы науки о сопротивлении материалов.

Деформация –изменения размера и формы тела под действием внешней нагрузки. Различают: упругие, пластические деформации.

Упругая деформация –способность элемента конструкции после снятия нагрузки возвращаться в исходное состояние.

Пластическая деформация – после снятия нагрузки элемент нагрузки не возвращается в исходное состояние, при этом остаются пластические, остаточные деформации.

Основные допущения сопромата (из лекций)

1. Материал конструкции считается однородным, т.е его свойство не зависит от величины рассматриваемого объема.

2. Материал заполняет весь объем непрерывно, т.е является сплошным (без пустот)

3. Материал считается изотропным т.е. свойство по всем направлениям одинакого.

4. Материалы обладают простейшими свойствами: упругостью, пластичностью, вязкостью.

При построении теории расчета невозможно отразить все многообразие свойств реальных материалов, поэтому приходится делать целый ряд допущений, упрощающих расчеты.

1. В курсе сопротивления материалов рассматривается идеализированное тело, которое считается сплошным (без пустот) и однородным.

2. Это означает, что свойства материала не зависят от формы и размера тела и одинаковы во всех его точках.

3. Упругие свойства материала во всех направлениях одинаковы, т.е. материал тела обладает упругой изотропией.

4. Тело считается абсолютно упругим, если после устранения причин, вызывающих деформацию, оно полностью восстанавливает свои первоначальные форму и размеры.

5. Это допущение справедливо лишь при напряжениях, не превышающих предел упругости.

6. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).

7. Закон Гука справедлив лишь при напряжениях, не превышающих предел пропорциональности.

8. Деформации элементов конструкции в большинстве случаев настолько малы, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояние от нагрузок до любых точек конструкции.

9. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности (принцип независимости действия сил).

10. Принцип независимости действия сил не распространяется на работу внешних и внутренних сил и на потенциальную энергию.

11. Поперечное сечение, плоское до деформации, остается плоским и после деформации (гипотеза плоских сечений Бернулли)

 

4. Метод сечений.

Метод сечений - метод механики, заключающийся в мысленном рассечении плоскостью твёрдого тела, находящегося в равновесии, отбрасывании одной из его частей и уравновешивании внешних сил, действующих на оставшуюся часть, внутренними усилиями, которые определяют из условий равновесия этой части

Чтобы правильно рассчитать конструкции на прочность и жесткость нужно уметь определять внутренние силы по заданным внешним нагрузкам, для этого используется метод сечений.

Внутренние силы- силы сцепления между смежными частицами тела, возникающие под действием внешней нагрузки. Именно внутренние силы определяют способность материала сопротивляться.

Метод сечения:

1. Допустим что тело находится в равновесии под действием внешних нагрузок.

2. Мысленно рассечем тело на две части и рассмотрим равновесие одной из них.

3. Для уравновешивания действие одной отброшенной части заменим внутренними силами (силами взаимодействия)

4. Введем систему координат, с началом в центре тяжести сечения. Ось z направим по нормам перпендикулярно плоскости сечения, а оси xy в плоскости сечения.

5. Спроецируем на эти оси внутренние силы и получим 6 ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ: N – нормальная продольная сила, Qx. Qy – поперечные силы, М кр- крутящий момент, Mx, My изгибающие моменты относительно осей x. y/

 

5. Понятие о напряжениях.

Метод сечения позволяет выявить внутренние силовые факторы, но для оценки прочности необходимо знать закон их распределения по сечению.

Если в сечении выделить бесконечно малую площадку F, то полагая внутренние силы действующими во всех точках сечения, можно сказать что на эту площадку придется и бесконечно малая сила Р. Отношение внутренней силы Р к величине выделенной площади F даст среднее напряжение на этой площадке Рср=P/F. Вводят численную меру интенивности внутренних сил – напряжение – это сила приходящая на единицу площади поперечного сечения.

По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела.

Сила имеет направление, напряжение также имеет направление.

s-(сигма) - нормальное напряжение, действует по нормали (перпендикуляру) к площадке; = p*sin a, стремится сблизить или удалитьотдельные части тела по направлению нормали плоскости сечения.

t-(тау) - касательные напряжения, они скользят по площадке, касаются ее = p *cos a стремится сдвинуть одни части относительно других по плоскости сечения. Поэтому касательные напряжения называют еще напряжением сдвига.

Р- полное напряжение

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону.

При определении напряжения в какой либо точке тела через эту точку можно провести бесконечное количество разно направленных плоскостей сечения. Надо знать помимо направления и величины напряжение, но и наклон площадки.

Интенсивность напряжения характеризуется деформацией.

 

6. Внутренние силовые факторы: виды нагружения, построение эпюр внутренних силовых факторов.

В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы.

По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений: надо мысленно рассечь брус, находящийся в равновесии, на две частии рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

Nz = N - продольная растягивающая (сжимающая) сила;

Mz = T - крутящий (скручивающий) момент;

Qx (Qy) = Q - поперечные силы;

Mx (My) = M - изгибающие моменты.

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

Для основных видов нагружения приняты следующие знаки:

Внутренняя продольная сила N принимается положительной, в случае если она стремится растянуть отсеченную часть бруса.

Внутренний скручивающий момент T принимается положительным, если он стремится повернуть рассматриваемое сечение против хода часовой стрелки, при взгляде на него со стороны отброшенной части бруса.

Внутренняя поперечная сила Q принимается положительной, если она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Внутренний изгибающий момент M принимается положительным, если он стремится сжать верхние слои балки.

При простейших случаях нагружения бруса в его поперечных сечениях возникает один внутренний силовой фактор

Если в поперечном сечении бруса имеет место только внутренняя продольная сила N, такая деформация называется растяжением/сжатием; На растяжение, сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки паровых машин и поршневых насосов, стяжные винты и другие детали.

Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые силы пытаются сдвинуть

Если в сечении бруса возникает только внутренний крутящий момент T, то такая деформация называется кручением (скручиванием); Кручение возникает при действии на стержень внешних сил, образующих моменты относительно продопьной оси стержня.

Изгиб - вид нагружения, при котором в поперечных сечениях бруса действует изгибающий момент M. Самый простой случай - это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с ппоскостью симметрии (ипи главной ппоскостью) балки.

Случай, когда в поперечных сечениях бруса есть только поперечная сила Q называется сдвиг.

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие сил в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики - эпюрами.

Эпюры внутренних силовых факторов, как правило, строят для того, чтобы наметить опасные сечения, т.е. сечения, в которых существует большая вероятность наступления разрушения из-за того, что там внутренние силовые факторы достигают наибольших значений.

Алгоритм построения эпюр ВСФ

1. Стержень разбить на участки (в пределах каждого участка внутренние силовые факторы изменяются по одной закономерности). Границами участков являются сечения, где:

- приложены внешние сосредоточенные усилия (сила, момент);

- начинается или заканчивается распределенная нагрузка;

- имеется перелом оси стержня.

2. В пределах каждого участка, применяя метод сечений и учитывая правило знаков, получить аналитическую зависимость (1.1) или (1.2) изменения каждого ВСФ (или, зная характер изменения ВСФ, определить его значения в граничных сечениях участка).

3. Построить графики (эпюры) этих зависимостей вдоль оси стержня, соблюдая следующие правила:

- провести базовую линию эпюры параллельно оси конструкции;

- ординаты эпюры в выбранном масштабе откладывать от базисной линии;

- в характерных (граничных) сечениях указать абсолютные значения ординат (без указания размерности);

- поле эпюры штриховать линиями, перпендикулярными базисной линии;

- знак ВСФ ставить в кружочке в положительной (+) и в отрицательной (-) областях эпюры;

- рядом с базисной линией нанести обозначение ВСФ и его размерность.

7. Напряжения в поперечных сечениях бруса. Закон Гука. Выбор допускаемых напряжений. Расчет на прочность при растяжении и сжатии.

При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения. Равнодействующая соответствующих элементарных сил σz dA - продольная сила N - может быть найдена с помощью метода сечений. Для того чтобы иметь возможность определить нормальные напряжения при известном значении продольной силы, необходимо установить закон их распределения по поперечному сечению бруса.

Эта задача решается на основе гипотезы плоских сечении (гипотезы Я. Бернулли), которая гласит: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.

При растяжении бруса (изготовленного, например, для большей наглядности опыта из резины), на поверхности которого нанесена система продольных и поперечных рисок, можно убедиться, что риски остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния: между поперечными рисками несколько увеличиваются, а между продольными — уменьшаются.

Описанный опыт можно рассматривать как подтверждение гипотезы плоских сечений; при этом предполагают, что внутри бруса деформации имеют тот же характер, что и на его поверхности.

Представим себе, что брус состоит из бесконечно большого числа продольных элементов, имеющих бесконечно малые («точечные») поперечные сечения. Эти элементы здесь и в дальнейшем будем условно называть волокнами.

Из гипотезы Бернулли следует, что все волокна в рассматриваемом случае деформируются одинаково. При однородном материале равным деформациям соответствуют одинаковые напряжения. Таким образом, приходим к заключению, что при растяжении (сжатии) бруса нормальные напряжения распределены по его поперечному сечению равномерно. Подчеркнем, что распределение напряжений не зависит от формы поперечного сечения.

Для нормальных напряжений принимают то же правило знаков, что и для продольных сил, т. е. при растяжении считают напряжения положительными.

 

Фактически распределение напряжений в сечениях бруса, примыкающих к месту приложения внешних сил, зависит от способа приложения нагрузки и может быть неравномерным. Экспериментальные и теоретические исследования показывают, что это нарушение равномерности распределения напряжений носит местный характер. В сечениях бруса, отстоящих от места нагружения на расстоянии, примерно равном наибольшему из поперечных размеров бруса, распределение напряжений можно считать практически равномерным.

 

Рассмотренное положение является частным случаем принципа Сен-Венана, который можно сформулировать следующим образом: распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения.

 

В частях, достаточно удаленных от места приложения сил, распределение напряжений практически зависит только от статического эквивалента этих сил, а не от способа их приложения.

 

Таким образом, применяя принцип Сен-Венана и отвлекаясь от вопроса о местных напряжениях, имеем возможность (как в этой, так и в последующих лекциях курса) не интересоваться конкретными способами приложения внешних сил. В местах резкого изменения формы и размеров поперечного сечения бруса также возникают местные напряжения. Это явление называют концентрацией напряжений, которую в этой лекции учитывать не будем.

 

В тех случаях, когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика - эпюры нормальных напряжений.

Закон Гука

Зако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком[1].

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Допускаемое напряжение - это отношение некоторого предельного напряжения для данного материала к коэффициенту запаса.

Номинальное допускаемое напряжение определяют по характеристикам материала при расчетной температуре.

В качестве некоторого предельного напряжения (т.е. характеристики материала) принимают - предел текучести, предел прочности, предел длительной прочности.

 

 

Расчёты на прочность ведутся по условиям прочности - неравенствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчётное напряжение не должно превышать допускаемое напряжение:

Расчётное напряжение зависит от нагрузки и размеров поперечного сечения, допускаемого только от материала детали и условий работы.

Существует три правила для расчёта на прочность.

1. Проектировочный расчёт - заданная расчётная схема и нагрузки; материал или размеры детали подбираются по величине можно подобрать марку материала. Определяется размер поперечного сечения материала, подбор материала.

2. Проверочный расчёт - известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.

3. Проверяется неравенство

8 Виды напряженного состояния.

Взаимодействие между частями элемента конструкции можно охарактеризовать величинами нормальных и касательных напряжений в каждой точке элемента. Эти величины зависят от направления сечения, проведенного через данную точку.

Совокупность нормальных и касательных напряжений, действующих по всем площадкам, проходящим через рассматриваемую точку, называется напряженным состоянием в этой точке.

При расчетах на прочность необходимо устанавливать напряженные состояния в опасных точках конструкции

Если через рассматриваемую точку тела нельзя провести ни одной площадки, в которой касательные и нормальные напряжения были бы равны нулю, то в этой точке имеется пространственное (трехосное) напряженное состояние. Если в одной (и только в одной) площадке, проходящей через рассматриваемую точку тела, касательные и нормальные напряжения равны нулю, то в этой точке имеется плоское (двухосное) напряженное состояние. Если касательные и нормальные напряжения равны нулю в двух площадках, проходящих через рассматриваемую точку тела, то в этой точке имеется линейное (одноосное) напряженное состояние; в таком случае касательные и нормальные напряжения равны нулю и во всех площадках, проходящих через линию пересечения указанных двух площадок.

 

Плоское и линейное напряженные состояния являются частными случаями пространственного напряженного состояния.

При пространственном напряженном состоянии нормальные напряжения по всем граням элементарного параллелепипеда, показанного на рис. 1.3, а, не равны нулю; при плоском напряженном состоянии нормальные напряжения по одной паре параллельных друг другу граней равны нулю (рис. 1.3, б), а при линейном — по двум парам таких граней (рис. 1.3, в).

9 Напряжения в наклонных площадках при линейном напряженном состоянии.

10. Напряжения в наклонных площадках при плоском напряженном состоянии. Виды геометрических характеристик.

 

 

Виды геометрических характеристик:

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации)

Геометрические характеристики плоских сечений

Здесь: C - центр тяжести плоских сечений;

A - площадь сечения;

Ix, Iy - осевые моменты инерции сечения относительно главных осей;

IxI, IyI - осевые моменты инерции относительно вспомогательных осей;

Ip - полярный момент инерции сечения;

Wx, Wy - осевые моменты сопротивления;

Wp - полярный момент сопротивления

Простейшими видами напряженного состояния стержневых элементов конструкции являются: растяжение, кручение и изгиб. Основные расчетные формулы для определения напряжений и деформаций в которых используются геометрические характеристики

* - N. Мк, Е, F, G, lз не изменяются вдоль оси стержня,

** - кручение стержней круглого поперечного сечения,

*** - прямой изгиб.

Правые части формул для расчета напряжений имеют идентичную структуру в виде дроби При этом в числителе стоят внутренние силовые факторы, а в знаменателе - геометрические характеристики поперечных сечений:

F - площадь поперечного сечения, Площадь сечения является одной из геометрических характеристик, используемых, главным образом, в расчетах на растяжение и сжатие. При расчетах на кручение, изгиб, а также на устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции, моменты сопротивления и т.д.

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси

Wp и Wx - полярный и осевой моменты сопротивления сечения.

При расчете деформаций в знаменателях формул также присутствуют геометрические характеристики сечений, например, lp и lx - полярный и осевой моменты инерции сечения.

Задача расчета этих величин осложняется тем, что все моменты сопротивления и моменты инерции сечений следует определять относительно главных центральных осей сечения. Следовательно, начинать расчет надо с определения координат центра тяжести сечения и выяснения какая пара осей, проходящая через него является главной.

При расчетах на устойчивость также будут встречаться геометрические характеристики сечений, а именно минимальный момент инерции.

Информацию о распределении внутренних силовых факторов в поперечных сечениях стержня вдоль его продольной оси при заданном нагружении обычно получают на основании соответствующих эпюр для продольных и поперечных сил, изгибающих и крутящих моментов.

Значения геометрических характеристик сечений могут быть получены двумя способами:

с помощью таблиц для профилей поперечных сечений стержней, принадлежащих к стандартному ряду промышленных изделий типа "уголок", "швеллер", "двутавр" и т.п.,

расчетным путем, исходя из конструктивных параметров для сечений нестандартного профиля или для составных сечений в виде комбинации сечений из числа стандартных профилей.

Простейшей характеристикой прочности и жесткости стержня, зависящей от формы и размеров поперечного сечения, является F - площадь поперечного сечения. Но эта величина используется непосредственно в расчетах лишь при равномерном распределении напряжений по поперечному сечению, т.е при растяжении или сжатии стержня.

При кручении и изгибе напряжения в сечении распределены неравномерно. Поэтому в расчетные формулы для напряжений входят не только геометрические характеристики сечения, но и дополнительные геометрические параметры, указывающие расположение тех точек сечения, где напряжения будут экстремальными при данном виде нагружения.

Рассмотримм это на примере стержня квадратного поперечного сечения, испытывающего деформацию изгиба (рис. 4.1,а).

Если высоту сть,.:кня увеличить вдвое, а ширину - уменьшить вдвое (рис. 4.1,6), то площадь поперечного сечения не изменится Деформация же свободного конца стержня в этом случае уменьшится по сравнению с исходным вариантом в 4 раза, а для разрушения стержня понадобится сила вдвое большая (по отношению к исходному варианту).

Если теперь повернуть стержень на 90° (рис. 4.1,в), то деформация его увеличится по сравнению с исходным вариантом (рис. 4.1,а) в 4 раза, а разрушающая сила уменьшится вдвое.

Вполне логичным представляется предположение о том, что уменьшение площади поперечного сечения уменьшает прочность стержня. Однако в ряде случаев удаление части материала стержня увеличивает его прочность.

Если у круглого сечения срезать сегменты, как показано на (рис. 4.2,а), то прочность стержня растет, достигая максимального значения, когда стрелка срезаемого сегмента равна 0,11 d.

Можно показать, что удаление вершин квадрата или треугольника (рис. 4.2,б,в) приводит к увеличению прочности на 5 %.

11. Моменты инерции и моменты сопротивления простейших фигур.

При определении сечения строительных конструкций очень часто необходимо знать момент инерции и момент сопротивления для рассматриваемого поперечного сечения конструкции.

Каждое тело, даже элементарно малое, имеет определенную массу, геометрические и прочностные характеристики, т.е. обязательно имеет центр тяжести и сопротивляется растяжению или сжатию. Эти прочностные характеристики называются сопротивлением материала сжатию или растяжению.

К числу простых плоских фигур относятся три фигуры: прямоугольник, треугольник и круг. Простыми эти фигуры считаются потому, что положение центра тяжести этих фигур заранее известно. Все остальные фигуры могут быть составлены из этих простых фигур и считаются сложными. Вычислим осевые моменты инерции простых фигур относительно их центральных осей.

12. Внутренние силовые факторы при кручении.

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно направленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круглого бруса (рис. 26.1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны Отброшенной части.

Внешний момент пары сил разворачивает участок бруса простив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.16). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы Образуют пару с моментом dm = pdQ; р — расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю: ΣdQ = 0

С помощью интегрирования получим суммарный момент силупругости, называемый крутящим моментом:

 

Практически крутящий момент определяется из условия равновесия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):

Σ mz = 0, т. е. -т + Mz = 0; Mz = т = Мк.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки

13. Классификация поперечных сечений стержней.

Стержень — тело удлиненной формы, два размера которого (высота и ширина) малы по сравнению с третьим размером (длиной)

В таком же значении иногда используют термин «брус», а термином «стержень» называют тела удлиненной формы, которое сопротивляются только усилиям сжатия и растяжения (в противоположность балке, которая работает преимущественно на изгиб).

Стержень условно представляется в виде совокупности параллельных или почти параллельных продольных волокон. Сечение стержня, нормальное волокнам, называется поперечным сечением.[3] Геометрическое место точек, проходящих через центры тяжести поперечных сечений, называется осью стержня.

Поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;

 

Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном

Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения

По относительным размерам в поперечном сечении различают массивные и тонкостенные стержни. Массивные стержни по форме поперечного сечения подразделяются на прямоугольные, круглые, тавровые, двутавровые, крестообразные и т. п. Тонкостенные стержни подразделяются на стержни с открытым и замкнутым поперечным сечением. Деление стержней на массивные и тонкостенные весьма условно. Главным отличительным признаком тонкостенных стержней является необходимость учета при их расчете на кручение депланации поперечного сечения.

14. Кручение стержня круглого и кольцевого поперечных сечений.

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

 

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

 

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

 

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

 

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

 

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

 

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

 

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

 

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Mk), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

 

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

 

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов, то угол поворота вала за 1 сек, выраженный в радианах, равен (П*n)/30 Работа крутящего момента Mk за 1 сек, т. е. мощность N, передаваемая валом, равна произведению величины момента на угол поворота вала (в радианах) за 1 сек:

 

где мощность N выражена в кГ∙м/сек.

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол, называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и

15. Кручение стержня тонкостенного замкнутого поперечного сечения.

В настоящее время в машиностроении, авиации, строительстве, железнодорожном транспорте все больше используются конструкции, выполненные из тонкостенных и штампованных профилей или просто из тонколистовой стали. Эти конструкции обеспечивают высокую жесткость и прочность при сравнительно небольшом весе, поэтому их применение в технике является весьма экономичным. На железнодорожном транспорте это элементы тележек, стенок локомотивов, вагонов и многих других конструкций.

Специфика расчета этих конструкций на прочность породила особую расчетную схему - схему тонкостенного стержня.

Основным признаком тонкостенного стержня является характерное отношение его геометрических размеров. В поперечном сечении одно из измерений (толщина) существенно меньше другого - срединной длины контура s. Последняя в свою очередь намного меньше, чем длина стержня l

Длина контура для тонкостенного стержня, s=h+2b.

 

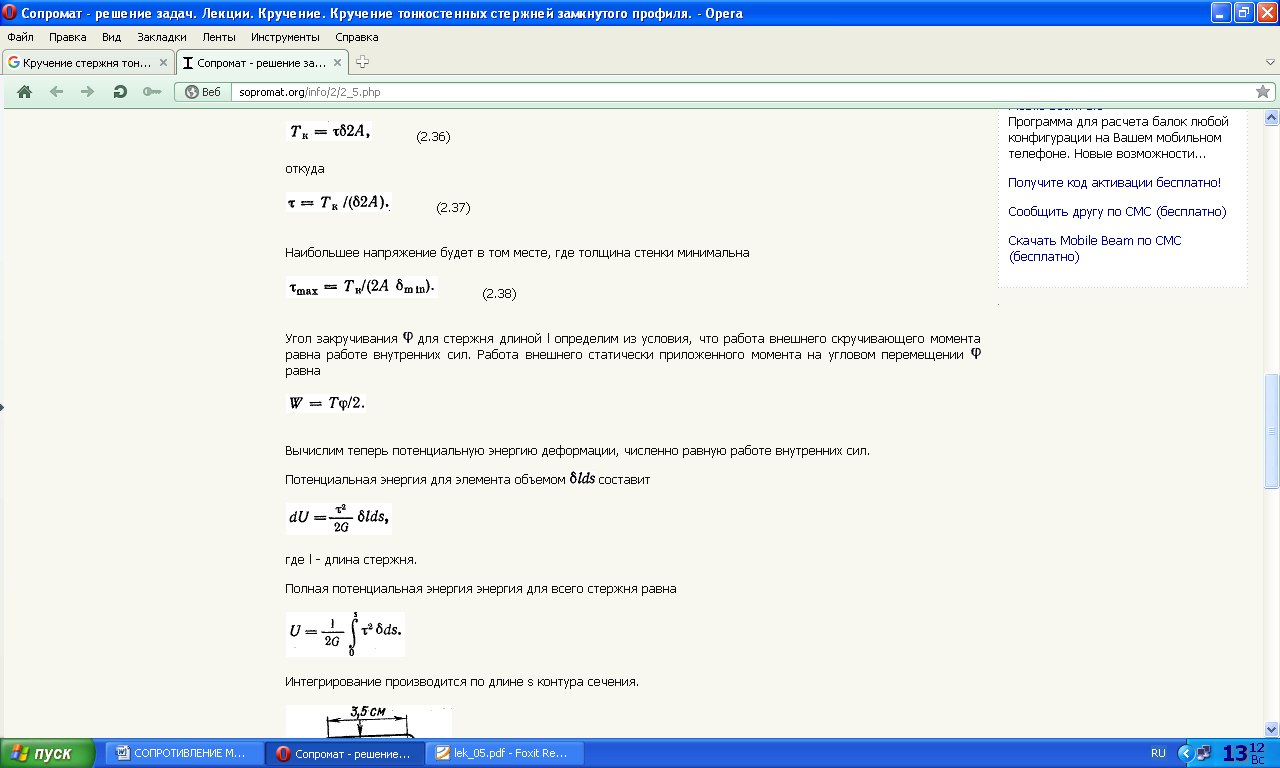
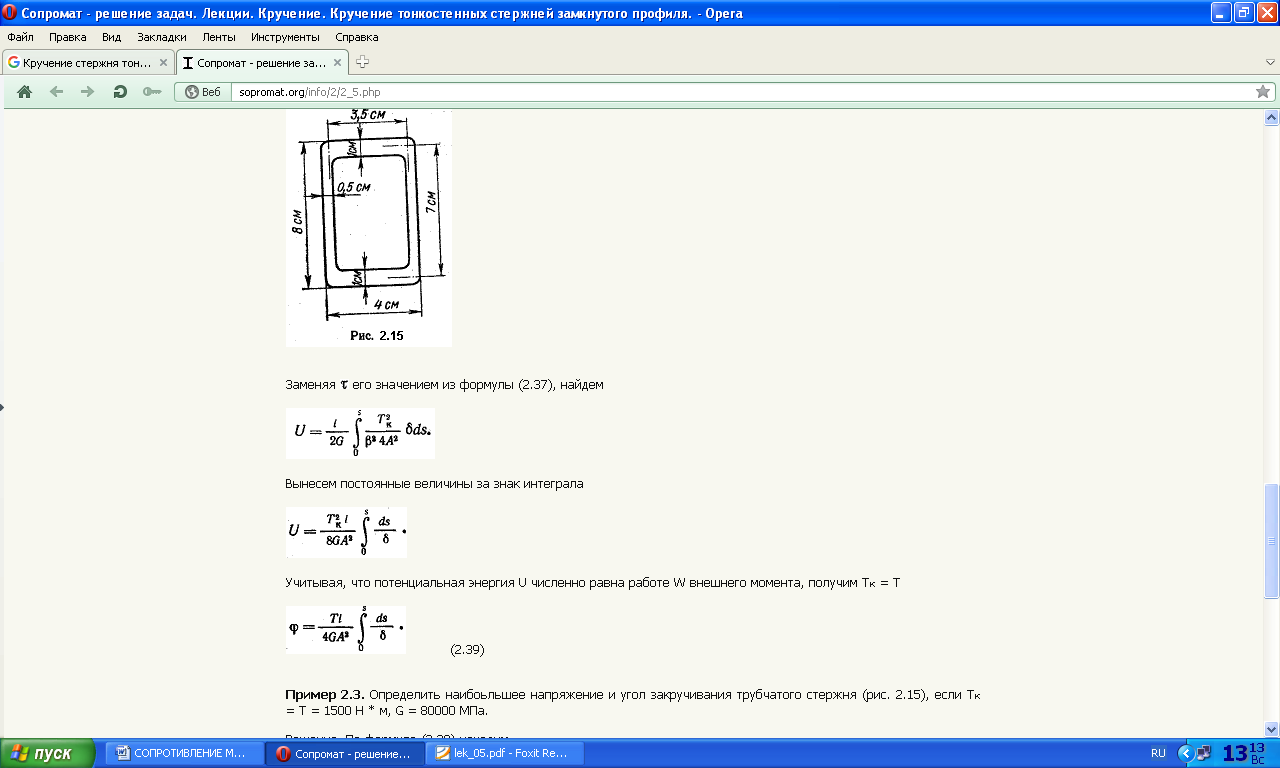
16. Кручение стержня сплошного прямоугольного сечения.

 

Поделиться: