Пример 1:
Исследовать и решить уравнение с параметром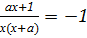 
D(y): 
Запишем уравнение в виде 
Коэффициент при х² равен 1, поэтому сразу найдем D₁.
1) 
Если D₁<0, то есть 
то уравнение не имеет корней;
если D₁=0, то есть 
то 
но т.к. 
уравнение не имеет корней;
если D₁>0, то есть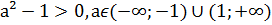 
то х₁,₂= 
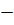а± 
.
2) Узнаем значение параметра а при х=0
если х=0, то 
т.е. нет таких а.
Ответ: при 
нет корней;
при а 
Пример 2:
Исследовать и решить уравнение с параметром 
D(y): 
Запишем уравнение в виде 
или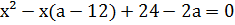 
1) 
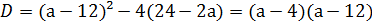
Если D<0, то есть 
то уравнение не имеет корней;
если D=0, то есть 
то х₁,₂= 
, т.е. при а 
при 
если D>0, то есть 
то х₁,₂= 
.
2) Узнаем значение параметра а при 
если 
если 
если 
т.е. нет такого а.
Ответ: при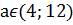 
нет корней;
при 
при
при 
при 
х₁,₂= .
Пример 3:
Исследовать и решить уравнение с параметром 
D(y): 
Запишем уравнение в виде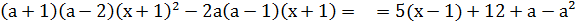 
1) 
или 
но 
по D(y), поэтому 
если 
2) 
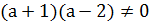
Если D<0, то есть 
нет таких а, при которых D<0;
если D=0, то есть 
то х₁,₂= 
, т.е. при 
если D>0, то есть 
, то х₁,₂= 
; х= 
, х=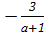 
.
3) Узнаем значение параметра а при х=1
если х=1,то 
т.е. а=5 или а= 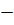4,
если 
если 
Ответ: при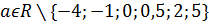 
х= , х= ;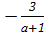
при 
нет корней;
при 
при
при 
при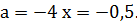 
Задания для тренировки:
Решить и исследовать уравнения с параметром:
1. 
;
2. 
;
3. 
;
4. 4(а-2)²х+4а(а-2)+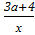 
=0;
5. 
;
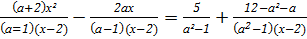6. 
;
7. (а-2)х²+2(а-3)х+а-5=0;
8. (а+5)х²+(2а-3)х+а-10=0;
9. 
;
10. 
.
Если на корни квадратного уравнения наложены условия
Случай 1
Когда оба корня больше параметра k
Решением уравнения является решение системы
Случай 2
Когда оба корня меньше параметра t
Решением уравнения является решение системы
Случай 3
Когда один корень больше, а другой меньше параметра h, то есть находятся по разные стороны от него
Решением уравнения является решение системы
Пример 1:
Найти все значения а, при каждом из которых корни квадратного трехчлена расположены по разные стороны от 1
Из условия видно, что 
После преобразований получаем
Рассмотрим функцию y= 
: график – парабола, вестви направлены вверх, с ох не пересекается.
Следовательно, у>0 при х∊R, 
;
Тогда решение системы зависит только от значения а при 
Решим неравенство с помощью координатной прямой
Ответ: при a∊(-4;-2)⋃(1;2).
Пример 2:
При каких значениях параметра оба корня уравнения больше 3?
Решением уравнения является решение системы
;
;
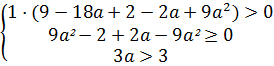Ответ: при 
Пример 3:
При каких значениях параметра k корни уравнения 
лежат в промежутке (0;3)?
Из условия видно, что
;
;
То есть, получаем систему неравенств, состоящую из двух систем.
;
Эту систему можно упростить, тогда получаем
;
;
;
k ∊ [2 
Ответ: при k ∊ [2 .
Задания для тренировки:
1. Найдите, при каких значениях параметра k оба корня уравнения 
(x₁≠x₂) меньше единицы.
2. Найдите, при каких значениях параметра k корни уравнения 
лежат между корнями уравнения 
3. Найдите, при каких значениях параметра k оба корня уравнения 
меньше 1 (x₁≠x₂).
4. Найдите, при каких значениях параметра k выполняется
,
5. Найдите, при каких значениях параметра k(-1;2)⊂(x₁;x₂),где 
выполняется 
=0.