Задание 1. Определение момента инерции 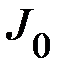 системы – «0»: вала и крестовины относительно оси вращения.
системы – «0»: вала и крестовины относительно оси вращения.
Порядок выполнения работы:
а) зафиксируйте систему с помощью тормоза в исходном положении так, чтобы донышко груза 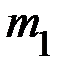 совпадало с верхним делением шкалы линейки;
совпадало с верхним делением шкалы линейки;
б) снимите систему с тормоза и одновременно включите секундомер;
в) в момент удара груза 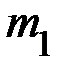 о площадку
о площадку 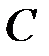 выключите секундомер, не останавливая движение системы. При этом вал по инерции продолжает вращаться и груз
выключите секундомер, не останавливая движение системы. При этом вал по инерции продолжает вращаться и груз 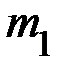 поднимается равнозамедленно до остановки на высоту
поднимается равнозамедленно до остановки на высоту 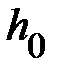 ;
;
г) в момент остановки зафиксируйте систему и измерьте высоту 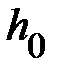 от площадки
от площадки 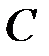 до донышка груза
до донышка груза 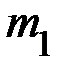 . Каждую из следующих величин: диаметр шкива вала
. Каждую из следующих величин: диаметр шкива вала 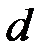 , время падения груза
, время падения груза 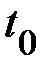 , высоту подъёма
, высоту подъёма 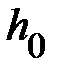 – найдите как среднее из трёх измерений, то есть весь опыт (пп. а, б, в, г) повторите три раза. Затем найдите соответствующие абсолютные ошибки: диаметра шкива
– найдите как среднее из трёх измерений, то есть весь опыт (пп. а, б, в, г) повторите три раза. Затем найдите соответствующие абсолютные ошибки: диаметра шкива 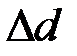 , времени падения груза
, времени падения груза 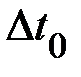 , высоты падения груза
, высоты падения груза 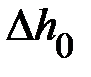 – как модуль среднего отклонения от среднего значения. Результаты измерений и вычислений запишите в табл. 1. По формуле (1) вычислите соответственно момент инерции
– как модуль среднего отклонения от среднего значения. Результаты измерений и вычислений запишите в табл. 1. По формуле (1) вычислите соответственно момент инерции  .
.
Задание 2. Нахождение момента инерции 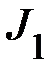 системы – «1»: вала, крестовины и двух тел массой
системы – «1»: вала, крестовины и двух тел массой 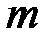 (каждое), симметрично расположенных на крестовине на расстоянии
(каждое), симметрично расположенных на крестовине на расстоянии 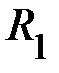 .
.
На крестовину диаметрально противоположно (на равном фиксированном расстоянии 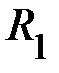 ) насадите два дополнительных тела массой
) насадите два дополнительных тела массой 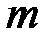 (каждое) и прочно закрепите их винтами. Проверьте балансировку системы, чтобы ни один из грузов не перетягивал. Далее трижды проделайте опыт, данные измерений времени падения
(каждое) и прочно закрепите их винтами. Проверьте балансировку системы, чтобы ни один из грузов не перетягивал. Далее трижды проделайте опыт, данные измерений времени падения 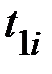 и высоты подъёма
и высоты подъёма 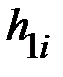 груза
груза 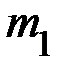 занесите в табл. 2. Затем по выражению (1) рассчитайте момент инерции
занесите в табл. 2. Затем по выражению (1) рассчитайте момент инерции 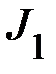 всей системы «1».
всей системы «1».
Задание 3. Определение моментов инерции 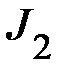 системы «2»: вала, крестовины и двух тел общей массой
системы «2»: вала, крестовины и двух тел общей массой 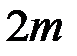 на расстояниях
на расстояниях 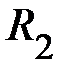 .
.
Как и в задаче 2, сначала через измерения диаметров 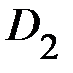 найдите фиксированные расстояния
найдите фиксированные расстояния 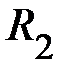 . Затем два тела диаметрально противоположно насадите на расстояние
. Затем два тела диаметрально противоположно насадите на расстояние 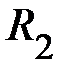 и трижды определите время падения
и трижды определите время падения 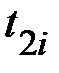 и высоту подъёма
и высоту подъёма 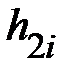 груза
груза 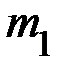 . По трём опытам для системы «2» измерьте среднее значение времени падения
. По трём опытам для системы «2» измерьте среднее значение времени падения 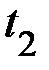 и среднее значение высоты подъёма
и среднее значение высоты подъёма 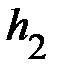 груза
груза 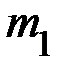 . Данные измерений занесите в табл. 3. Для тел на расстоянии
. Данные измерений занесите в табл. 3. Для тел на расстоянии 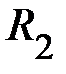 по формуле (1) вычислите моменты инерции
по формуле (1) вычислите моменты инерции 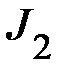 .
.
Задание 4. Сравнение теоретического значения момента инерции тела  с опытным
с опытным  .
.
По формуле 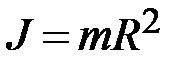 вычислите теоретические значения моментов инерции
вычислите теоретические значения моментов инерции 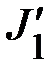 ,
, 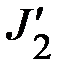 тел относительно оси вращения, находящихся соответственно на расстояниях
тел относительно оси вращения, находящихся соответственно на расстояниях 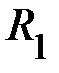 ,
, 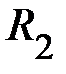 считая их материальными точками.
считая их материальными точками. 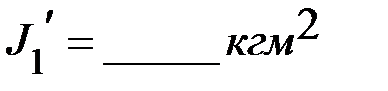 .
. 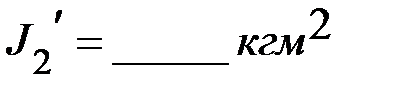 .
.
Таблица 1.
| Опыт | 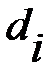 , , 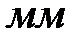
| 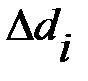 , , 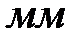
| 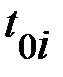 , , 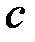
| 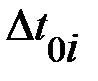 , , 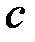
| 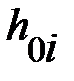 , , 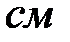
| 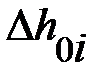 , , 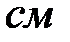
|
| Среднее | 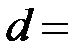
| 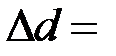
| 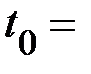
| 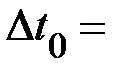
| 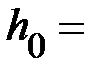
| 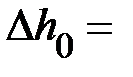
|
Диаметр шкива вала 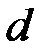 , время падения
, время падения 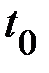 , высота подъёма
, высота подъёма 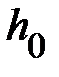 груза
груза 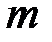 и соответственно ошибки
и соответственно ошибки 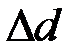 ,
, 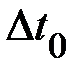 ,
, 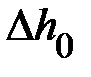 системы «0»: вала и крестовины.
системы «0»: вала и крестовины.
Момент инерции системы «О» вычисляют по формуле (1). 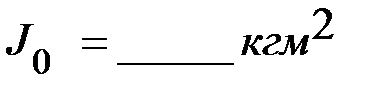 .
.
Таблица 2.
| Опыт | 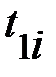 , , 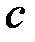
| 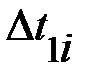 , , 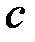
| 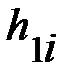 , , 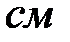
| 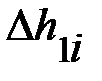 , , 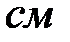
|
| Среднее | 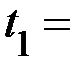
| 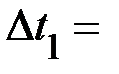
| 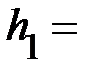
| 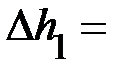
|
Время падения 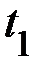 , высота подъёма
, высота подъёма 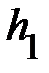 груза
груза 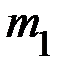 и абсолютные ошибки
и абсолютные ошибки 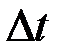 и
и 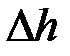 системы «1»: вала, крестовины и двух тел общей массой
системы «1»: вала, крестовины и двух тел общей массой 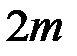 на расстоянии
на расстоянии 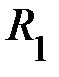 . Момент инерции системы «1» равен
. Момент инерции системы «1» равен 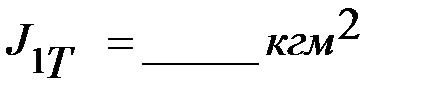 . Момент инерции двух тел (Т) на расстоянии
. Момент инерции двух тел (Т) на расстоянии 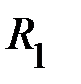 равен
равен
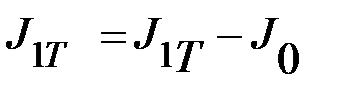 = кгм2
= кгм2
Таблица 3.
| Опыт | 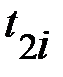 , , 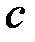
| 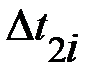 , , 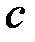
| 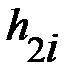 , , 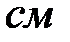
| 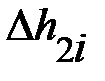 , , 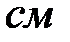
|
| Среднее | 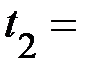
| 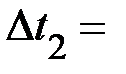
| 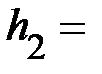
| 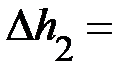
|
Время падения 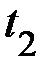 , высота подъёма
, высота подъёма 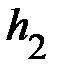 груза
груза 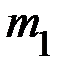 и абсолютные ошибки
и абсолютные ошибки 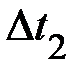 ,
, 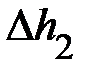 системы «2»: вала, крестовины и двух тел общей массой
системы «2»: вала, крестовины и двух тел общей массой 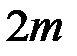 на расстоянии
на расстоянии 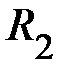 . Момент инерции системы «2» равен
. Момент инерции системы «2» равен 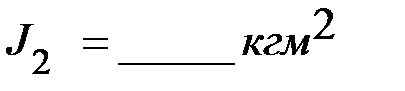 . Момент инерции двух тел (Т) на расстоянии
. Момент инерции двух тел (Т) на расстоянии 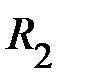 равен.
равен.
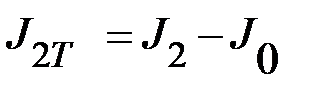 = кгм2
= кгм2
Выводы.
1. Момент инерции системы «0» вала с шкивом, крестовины 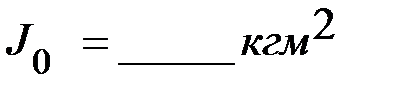 .
.
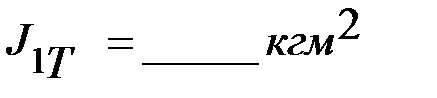
2. Момент инерции двух тел, находящихся на расстоянии 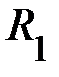 .
. 
3. момент инерции дух тел, находящихся на расстоянии 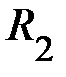 .
. 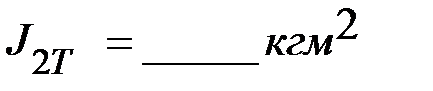
4. Теоретические значения моментов инерции двух тел на расстоянии 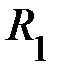 и
и 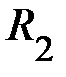 равны соответственно,
равны соответственно, 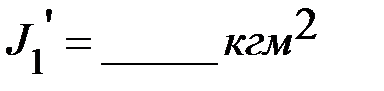 ,
, 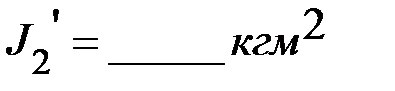 .
.
5. Отношение моментов инерции (2/1) двух тел, полученных в ходе эксперимента, к соответствующему отношению рассчитанному (теоретическому): 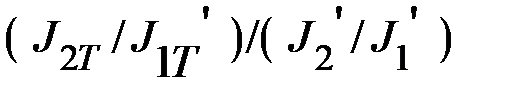 =
=
6. Отношение моментов инерции (2/1) двух тел, полученных в ходе опыта, соответствуют отношению квадрату времени падении груза:
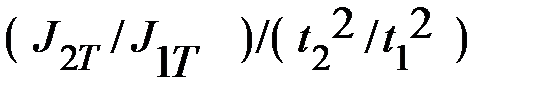 =
=
Составление отчёта. Отчёт составьте по схеме: 1) цель работы, 2) приборы и принадлежности, 3) схема установки, 4) расчётная формула с пояснением физических величин и их размерностей, 5) таблицы измерений, 6) расчёты определяемых величин и их погрешностей, 7) правильно записанные окончательные результаты.
Контрольные вопросы: 1.Запишите формулы и размерности физических величин, которые характеризуют вращательное движение твёрдого тела вокруг неподвижной оси: угла поворота 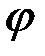 , угловой скорости
, угловой скорости  , углового ускорения
, углового ускорения 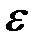 , момента силы
, момента силы 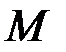 , момента инерции
, момента инерции  , момента импульса
, момента импульса 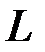 .
.
2. Запишите по аналогии формулы и размерности физических величин, которые характеризуют прямолинейное движение твёрдого тела.
3. Нарисуйте схему установки маятника Обербека.
4. Выведите формулу для расчёта момента силы 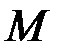 натяжения нити
натяжения нити 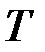 , углового ускорения
, углового ускорения 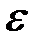 , момента силы трения
, момента силы трения 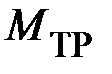 , момента инерции
, момента инерции  вращающейся системы (с учётом и без учёта силы трения).
вращающейся системы (с учётом и без учёта силы трения).
5.Каким образом, пользуясь маятником Обербека, можно проверить основной закон динамики вращательного движения?
Маятник Обербека. Задаваемые параметры: 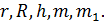 Запишите изменения определяемых параметров врашения тел:
Запишите изменения определяемых параметров врашения тел: 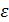 ,
, 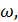
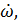
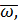
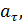 υ,
υ, 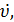
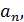
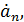
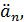
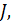 L,
L, 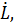
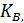
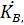
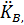 M, N,
M, N, 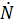 .
.
ЗВД 1. Сплошной шар, полый тонкостенный цилиндр, сплошной цилиндр массой m, радиусом r вращается с переменным ускорением ε (ω 0 = 0). Уравнение вращения тела имеет вид 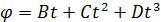 , где B = 0,5 рад/с, C = 0,5 рад/с2, D = 0,5 рад/с3. Тело вращается вокруг центра масс. В момент времени t вычислите следующие параметры: 1) L – момент импульса (кгм2/с) вращения тела, 2) К В – кинетическую энергию (Дж) вращения тела, 3)
, где B = 0,5 рад/с, C = 0,5 рад/с2, D = 0,5 рад/с3. Тело вращается вокруг центра масс. В момент времени t вычислите следующие параметры: 1) L – момент импульса (кгм2/с) вращения тела, 2) К В – кинетическую энергию (Дж) вращения тела, 3) 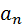 – ускорение (м/с2), направленное по нормали, 4) N – мощность вращения тела (Вт), 5) М – момент силы (кгм2/с2) вращения тела. Дано: m = 1 кг, r = 0,1 м, угловое ускорение тела ε t = 25 c –1 → t.
– ускорение (м/с2), направленное по нормали, 4) N – мощность вращения тела (Вт), 5) М – момент силы (кгм2/с2) вращения тела. Дано: m = 1 кг, r = 0,1 м, угловое ускорение тела ε t = 25 c –1 → t.
ЗВД 2. Сплошной шар, полый тонкостенный цилиндр, сплошной цилиндр массой m, радиусом r вращается с переменным ускорением ε (ω 0 = 0). Уравнение вращения тела имеет вид 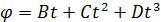 , где B = 0,5 рад/с, C = 0,5 рад/с2, D = 0,5 рад/с3. Тело вращается вокруг центра масс. В момент времени t вычислите следующие параметры: 1)
, где B = 0,5 рад/с, C = 0,5 рад/с2, D = 0,5 рад/с3. Тело вращается вокруг центра масс. В момент времени t вычислите следующие параметры: 1) 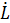 – скорость изменения момента импульса (кгм/с2) вращения тела, 2)
– скорость изменения момента импульса (кгм/с2) вращения тела, 2) 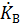 – скорость изменения кинетической энергии (Вт) вращения тела, 3)
– скорость изменения кинетической энергии (Вт) вращения тела, 3) 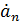 – скорость изменения ускорения (м/с3), направленного по нормали, 4)
– скорость изменения ускорения (м/с3), направленного по нормали, 4) 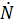 – скорость изменения мощности (Вт/с) вращения тела, 5)
– скорость изменения мощности (Вт/с) вращения тела, 5) 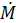 – скорость изменения момента силы (кгм2/с3) вращения тела. Дано m = 1 кг, r = 0,1 м, угловое ускорение тела ε t = 25 c –1 → t.
– скорость изменения момента силы (кгм2/с3) вращения тела. Дано m = 1 кг, r = 0,1 м, угловое ускорение тела ε t = 25 c –1 → t.
ЗВД 5. Маятник Обербека. Масса груза 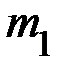 , масса тела
, масса тела 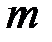 (где m1 ≥ m), высота опускания груза
(где m1 ≥ m), высота опускания груза 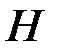 , радиус вала
, радиус вала 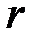 , радиус вращения тел
, радиус вращения тел 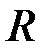 . Груз, опускаясь (
. Груз, опускаясь (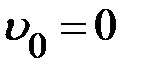 ) вращает тела. Масса блока m' << m. Моменты сил М1 > М. Трением пренебречь. В опыте меняют радиус вращения тел
) вращает тела. Масса блока m' << m. Моменты сил М1 > М. Трением пренебречь. В опыте меняют радиус вращения тел 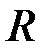 ∼на крестовине. Не меняют r =, m =, m 1 =. В первом опыте R 1 = r. Во сколько раз изменятся максимальные значения параметров вращения тел: 1) L – момент импульса, 2) К В – кинетическая энергия, 3) N – мощность вращения, 4)
∼на крестовине. Не меняют r =, m =, m 1 =. В первом опыте R 1 = r. Во сколько раз изменятся максимальные значения параметров вращения тел: 1) L – момент импульса, 2) К В – кинетическая энергия, 3) N – мощность вращения, 4) 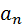 – ускорение, направленное по нормали, 5) М – момент сил вращения тел, если во втором опыте скорость изменения мощности вращения блока
– ускорение, направленное по нормали, 5) М – момент сил вращения тел, если во втором опыте скорость изменения мощности вращения блока 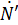 ↓ 16, угловая скорость блока ω ↓ 4, R 2 ↑ 2, m =, r =?
↓ 16, угловая скорость блока ω ↓ 4, R 2 ↑ 2, m =, r =?
ЗВД 6. Маятник Обербека. Масса груза 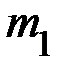 , масса тела
, масса тела 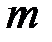 (где m1 ≥ m), высота опускания груза
(где m1 ≥ m), высота опускания груза 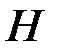 , радиус вала
, радиус вала 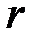 , радиус вращения тел
, радиус вращения тел 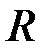 . Груз, опускаясь (
. Груз, опускаясь (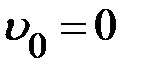 ) вращает тела. Масса блока m' << m. Моменты сил М1 > М. Трением пренебречь. В опыте меняют радиус вращения тел
) вращает тела. Масса блока m' << m. Моменты сил М1 > М. Трением пренебречь. В опыте меняют радиус вращения тел 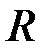 ∼на крестовине. Не меняют r =, m =, m 1 =. В первом опыте R 1 = r. Во сколько раз изменятся максимальные значения параметров вращения тел: 1)
∼на крестовине. Не меняют r =, m =, m 1 =. В первом опыте R 1 = r. Во сколько раз изменятся максимальные значения параметров вращения тел: 1) 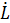 – скорость изменения момента импульса, 2)
– скорость изменения момента импульса, 2) 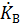 – скорость изменения кинетической энергии, 3)
– скорость изменения кинетической энергии, 3) 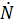 – скорость изменения мощности вращения, 4)
– скорость изменения мощности вращения, 4) 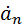 – скорость изменения ускорения, направленного по нормали, 5)
– скорость изменения ускорения, направленного по нормали, 5) 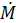 – скорость изменения момента сил вращения, если во втором опыте скорость изменения мощности вращения блока
– скорость изменения момента сил вращения, если во втором опыте скорость изменения мощности вращения блока 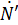 ↓ 16, угловая скорость блока ω ↓ 4, R 2 ↑ 2, m =, r =?
↓ 16, угловая скорость блока ω ↓ 4, R 2 ↑ 2, m =, r =?