Одним из простейших движений твёрдого тела является его вращение вокруг оси, неподвижной в некоторой инерциальной системе отсчёта. При таком движении траектории различных точек тела представляют собой окружности с центрами на оси в плоскостях, перпендикулярных оси.
Кинематические характеристики вращательного движения: угол поворота, угловая скорость, угловое ускорение.
Положение тела, вращающегося вокруг неподвижной оси, характеризуется единственной величиной – углом поворота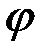 
относительно некоторого начального положения (угловой координатой). В процессе вращения угол поворота изменяется с течением времени, 
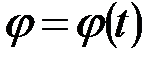. Угол поворота 
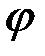измеряется в радианах.
Быстрота вращения характеризуется угловой скоростью 
, которая представляет собой первую производную от угла поворота по времени 
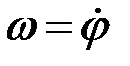. Угловая скорость 
измеряется в рад/с.
Быстрота изменения угловой скорости характеризуется угловым ускорением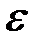 
, которое представляет собой первую производную от угловой скорости по времени (или вторую производную от угла поворота по времени) 
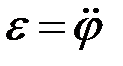. Угловое ускорение 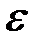измеряется в рад/с 
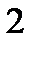. При равномерном вращении 
; 
; 
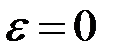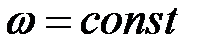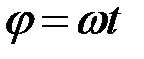. При равноускоренном вращении из состояния покоя 
; 
; 
.
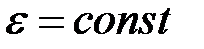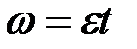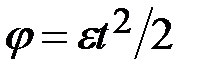Динамические характеристики вращательного движения: момент силы, момент инерции, момент импульса. Второй закон динамики вращательного движения.
Вращающее действие силы характеризуется моментом силы М относительно оси вращения. Момент силы относительно неподвижной точки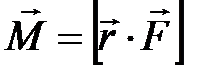 
, где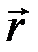 
– радиус вектор, проведенный из этой точки в точку приложения силы 
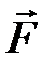. Модуль момента силы 
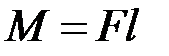, где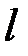 
– плечо силы (кратчайшее расстояние между линией действия силы и осью вращения). В случае, когда вектор силы перпендикулярен оси, момент силы равен произведению силы на плечо, то есть на расстояние от оси вращения до линии действия силы 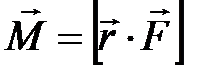. В системе СИ момент силы М измеряется в 
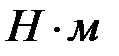. Если на тело действует несколько сил, векторы которых лежат в плоскости, перпендикулярной оси вращения, то результирующий момент силы равен алгебраической сумме моментов отдельных сил 
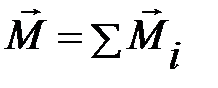. При этом моменты сил, стремящихся вращать тело в противоположных направлениях, входят в алгебраическую сумму с противоположными знаками.
|
|
Инертность тела при вращательном движении характеризуется моментом инерции 
этого тела относительно оси. Моментом инерции материальной точки относительно оси называют произведение массы материальной точки на квадрат её расстоянии от оси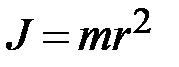 
. Твёрдое тело конечных размеров можно рассматривать как систему жёстко связанных между собой материальных точек. При этом момент инерции тела относительно оси равен сумме моментов инерции всех материальных точек, образующих тело, относительно той же оси 
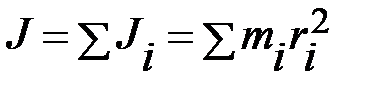. В системе СИ момент инерции измеряется в 
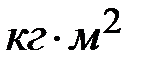. Момент инерции тела зависит от его массы, положения оси и от того, как она распределена относительно оси.
Работа при вращении тела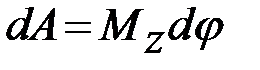 
, где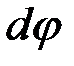 
– угол поворота тела;
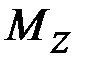– момент силы относительно оси 
.
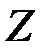Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси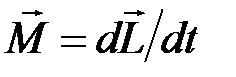 
или 
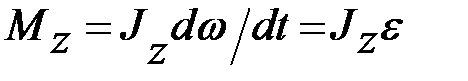, где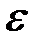 
– угловое ускорение, 
– момент инерции тела относительно оси .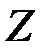
Закон сохранения момента импульса (момента количества движения) для замкнутой системы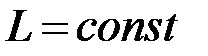 
.
Моментом импульса тела L относительно оси называют произведение момента инерции тела на его угловую скорость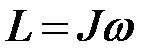 
. В системе СИ момент импульса L измеряется в 
.
|
|
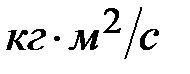Полезно запомнить, что формулы механики поступательного и вращательного движения очень похожи, только при вращательном движении вместо линейных кинематических величин (пути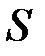 
, скорости 
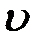, ускорения 
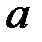) используют соответствующие угловые величины (угол поворота 
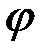, угловую скорость 
, угловое ускорение 
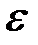), а вместо динамических величин (силы 
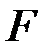, массы 
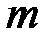, импульса 
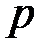) – их моменты (момент силы 
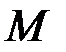, момент инерции 
, момент импульса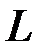 
). Аналогичны также формулы кинетической энергии при поступательном 
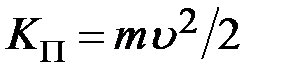и вращательном 
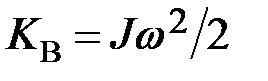движениях.
Для проведения инженерных расчётов в самых различных областях техники (электропривод, робототехника, механика и т.д.) надо знать моменты инерции вращающихся элементов конструкций. Теоретически рассчитать их можно лишь в немногих простейших случаях. В связи с этим возникает необходимость опытного определения моментов инерции тел.