Конструктивная семантика для СКИП.
Произвольнуюформулу F конструктивного исчисления предикатов мы будем рассматривать как спецификацию (точное описание) некоторой задачи Z. Формулу F будем считать истинной, если мы сможем предъявить решение задачи Z.
Формула F&G истинна, когда мы можем построить терм вида
<tF, tG>, где tF -решение F, tG -решение G.
Формула F 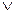 G истинна, когда мы можем построить терм вида
G истинна, когда мы можем построить терм вида
<0, tF> или  <1, tG>, где tF -решение F, tG -решение G..
<1, tG>, где tF -решение F, tG -решение G..
Формула F  G истинна, когда имеется решение задачи G с некоторым параметром типа F (т.е. по любому решению задачи F можно построить решение задачи G):
G истинна, когда имеется решение задачи G с некоторым параметром типа F (т.е. по любому решению задачи F можно построить решение задачи G): 
 xF. tG (xF ).
xF. tG (xF ).
Формула 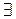 x0 F(x0)истинна, когда существуют конкретный объект a0 и решение tF(a), т.е мы можем построить терм вида < a0, tF(a)>.
x0 F(x0)истинна, когда существуют конкретный объект a0 и решение tF(a), т.е мы можем построить терм вида < a0, tF(a)>.
Формула 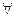 x0 F(x0) истинна, когда для любого объекта x0 можно построить решение задачи F(x0), т.е мы можем построить терм вида
x0 F(x0) истинна, когда для любого объекта x0 можно построить решение задачи F(x0), т.е мы можем построить терм вида  x0 . tF(
x0 . tF(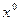 ).
).
Конструктивное понятие отрицания:
Константа ложь f или 0=1.

Идея построения правильных программ:
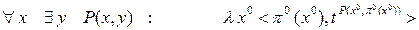
Цель следующего определения ввести синтаксическое понятие «замкнутый  - терм типа F», таким образом, чтобы конструктивная истинность определялась следующим образом: формула F - истинна тогда и только тогда, когда существует замкнутый
- терм типа F», таким образом, чтобы конструктивная истинность определялась следующим образом: формула F - истинна тогда и только тогда, когда существует замкнутый  - терм типа F.
- терм типа F.
6.2. Определение замкнутого 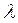 -терма.
-терма.
0). Пусть tf – произвольный  -терм типа f. Тогда для любой формулы А терм tf также будем считать термом типа А.
-терм типа f. Тогда для любой формулы А терм tf также будем считать термом типа А.
1).ПустьA- произвольная формула конструктивного исчисления предикатов, тогда xA является  -термом типа А, при этом переменная xA в
-термом типа А, при этом переменная xA в  -терм xA входит свободно.
-терм xA входит свободно.
2). Пусть tA – произвольный  -терм типа А,Sb – произвольный
-терм типа А,Sb – произвольный  -терм типа В, тогда
-терм типа В, тогда
< tA, Sb >=r A&B
является  -термом типа А&В, при этом все свободные переменные термов tA, Sbявляются свободными переменнымии в
-термом типа А&В, при этом все свободные переменные термов tA, Sbявляются свободными переменнымии в  -терме r A&B типа А&В.
-терме r A&B типа А&В.
3). Пусть tA – произвольный  -терм типа А,Sb – произвольный
-терм типа А,Sb – произвольный  -терм типа В, тогда
-терм типа В, тогда
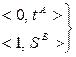 = r A
= r A  B
B
является  -термом типа А
-термом типа А 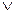 В, при этом все свободные переменные термов tA, Sbявляются свободными переменнымии в
В, при этом все свободные переменные термов tA, Sbявляются свободными переменнымии в  -терме r A
-терме r A 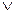 B типа А
B типа А 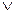 В.
В.
4). Пусть tB (xA)- терм, в который входит свободно переменная xA типа А, тогда
 xА. tВ (xА )= r A
xА. tВ (xА )= r A  B
B
является  -термом типа А
-термом типа А  В, при этом все свободные переменные терма tB, за исключением переменной xA, являются свободными переменнымии в
В, при этом все свободные переменные терма tB, за исключением переменной xA, являются свободными переменнымии в  -терме r A
-терме r A  B типа А
B типа А  В.
В.
5). Пусть t0- объектный терм, SA( ) -терм, тогда
) -терм, тогда
<t0, SA(  ) >= r
) >= r 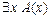
является  -термом типа
-термом типа  , при этом все свободные переменные терма SA(
, при этом все свободные переменные терма SA( ) являются свободными переменнымии в
) являются свободными переменнымии в  -терме r
-терме r 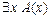 типа
типа  .
.
6). Пусть tA(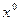 ) -терм, x0-объектная переменная, тогда
) -терм, x0-объектная переменная, тогда
 x0. tA(
x0. tA( 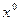 ) = r
) = r 
является  -термом типа
-термом типа  , при этом все свободные переменные терма tA(
, при этом все свободные переменные терма tA(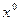 ), за исключением переменной x0, являются свободными переменнымии в
), за исключением переменной x0, являются свободными переменнымии в  -терме r
-терме r  типа
типа  .
.
7а). Пусть t A&B - терм типа А&B, тогда
(t A&B)0 = rA,
является термом типа A, при этом все свободные переменные терма t A&Bявляются свободными переменными и в терме rA.
7б). Пусть tA&B терм типа A&B, тогда
(t A&B)1 =rВ,
является термом типа B, при этом все свободные переменные терма tA&B являются свободными переменными и в терме rВ.
8а). Пусть t 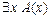 - терм типа
- терм типа 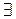 x A(x), тогда
x A(x), тогда
(t 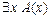 )0 = r0,
)0 = r0,
является объектным термом, при этом все свободные переменные терма t 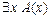 являются свободными переменными и в терме r0.
являются свободными переменными и в терме r0.
8б). Пусть t 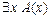 - терм типа
- терм типа 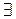 x A(x), тогда
x A(x), тогда
(t 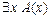 )1 = rA(
)1 = rA(  ), где S0= (t
), где S0= (t 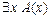 )0,
)0,
является термом типа A(S0), при этом все свободные переменные терма t 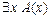 являются свободными переменными и в терме rA(
являются свободными переменными и в терме rA( ).
).
9а). Пустьt A  B - терм типа A
B - терм типа A  B, SA - терм типа A, тогда
B, SA - терм типа A, тогда
t A  B[SA] = rB,
B[SA] = rB,
является термом типа B, при этом все свободные переменные термов t A  B и SA являются свободными переменными в терме rB.
B и SA являются свободными переменными в терме rB.
9б). Пусть t  - терм типа
- терм типа 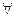 x A(x), S0 - объектный терм, тогда
x A(x), S0 - объектный терм, тогда
t  [S0] = rA(
[S0] = rA(  ),
),
является термом типа A(S0), при этом все свободные переменные терм t  являются свободными переменными и в терме rA(
являются свободными переменными и в терме rA( ).
).
10). ПустьtA, SA – термы типа A, u0, v0 – объектные термы, тогда
(if u0 = v0 then tA else SA) =rA,
является термом типа A, при этом все свободные переменные термов tA, SA, u0, v0 являются свободными переменными в терме rA.
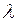 -терм называется замкнутым, если он не содержит свободных переменных.
-терм называется замкнутым, если он не содержит свободных переменных.