Пропускная способность дискретных каналов с шумами

Пропускная способность дискретного (цифрового) канала

 

Структурная схема цифрового информационного канала показана на рис.1 [1,2].

 

 

 

Рис.1. Структурная схема цифрового канала

На вход такого канала обычно поступают дискретные соотношения х, например, в виде текста. Последние с помощью кодирующего устройства преобразуются в кодированные сигналы у. Как известно, для кодирования используется некоторый алфавит элементарных сигналов (символов) – у₁, у₂,…, у_m, а существо кодирования сводится к представлению отдельных сообщений х_i или последовательностей сообщений некоторыми комбинациями символов используемого алфавита. Декодирующее устройство преобразует кодированные сигналы z в сообщения w в форме, наиболее приемлемой для получателя, которым может быть не только человек, но и различные технические устройства (принтер, монитор, ПЭВМ и др.). В современных информационно-вычислительных комплексах исходные сообщения х могут быть и в непрерывной форме, но с помощью кодирующих устройств последние преобразуют в кодированные сигналы.

В реальных каналах неизбежны различного рода помехи, представленные на рис.1 в виде источника помех, которые нередко называют шумом. Термин «шум» впервые, видимо, появился применительно к телефонным каналам, в которых помехи воспринимались «на слух». Эти каналы в настоящее время широко используются не только по прямому назначению, но и для передачи цифровых данных в информационных системах.

Пропускная способность дискретных (цифровых) каналов

При отсутствии шумов

При отсутствии шумов можно считать, что в информационном канале z = y, а w = x, следовательно, для сообщений z_T = y_T, w_T = x_T, передаваемых за время Т, количество информации, поступающей к получателю от источника, составит

I(W_T, X_T) = I(X_T, X_T) = H(X_T),

где Н(Х_Т) - энтропия источника сообщений.

По аналогии для канала связи, представляющего часть информационного канала, будем иметь

I(Z_T,Y_T) = I(Y_T, Y_T) = H(Y_T). (1.1)

Если последовательность х_Т состоит из m сообщений и средняя длительность сигнала, обеспечивающего передачу одного сообщения составляет t_с, то можно определить скорость передачи информации как

, (1.2)

где Н(X) – энтропия источника n сообщений:

.

В дальнейшем основание 2 логарифма для простоты будет опущено.

Очевидно, что скорость передачи информации будет зависеть от статистических характеристик источника сообщений, метода кодирования сообщений и свойств канала. Так, при одном и том же способе кодирования длительность символов передаваемых сигналов может быть различной в зависимости от ширины полосы частот пропускания канала. С изменением длительности символов меняется и скорость передачи информации.

Пропускная способность информационного канала C определяется максимальным значением скорости передачи:

Аналогично находится пропускная способность канала связи C _с, являющегося частью информационного канала:

(1.3)

Обычно C_с > C.

Реальная скорость передачи информации может быть максимальной и равной пропускной способности канала, если статистические характеристики источника сообщений определенным образом согласованы со свойствами информационного канала. Для каждого источника это может быть достигнуто специальным выбором способа кодирования сообщений. Такое кодирование, при котором достигается наиболее эффективное использование пропускной способности дискретного канала (т.е. обеспечивается максимальная скорость передачи информации _макс), называется эффективным.

Дискретный канал, в котором передаваемые сообщения представлены двоичным кодом, называется двоичным каналом. Если код имеет m символов (разрядов), то очевидно, что всего можно закодировать n = 2^m сообщений, а длительность одного сообщения составит T = mt, где t - длительность символа кода с учетом того, что все символы обычно имеют одинаковую длительность. Двоичные коды, состоящие из одинакового числа символов m, называются равномерными. Пропускная способность рассматриваемого канала с учетом формул (1.1), (1.2) и (1.3) составит

(1.4)

Выражение (1.4) принимает максимальное значение, когда энтропия ансамбля событий (сообщений) H(Y_T) будет наибольшей. Из свойств энтропии следует, что H(Y_T) будет максимальна, если сообщения равновероятны, это максимальное значение может быть определено мерой Хартли и будет равно logn = log2^m = m [2].

Следует, однако, иметь ввиду, что фактическая скорость передачи информации не всегда оказывается равной пропускной способности канала.

Рассмотрим два простых примера.

Пример 1. Пусть источник сообщений вырабатывает четыре сообщения х₁, х₂, х₃, х₄, (n = 4). Все сообщения имеют одинаковые вероятности: P(x_i) = 1/n = 0,25. Для их кодирования используется двоичный равномерный код, число символов в котором достаточно выбрать m = 2. Исходные сообщения х₁, х₂, х₃, х₄ в этом примере будут представлены следующими кодами: 00, 01, 10, 11.

Скорость передачи информации будет определяться по формуле (1.2), в которой энтропия источника равновероятных сообщений будет максимальной:

а длительность каждого из четырех сообщений будет определяться длительностями соответствующих кодовых комбинаций и составит t_с = 2t. Для примера 1 по формуле (1.2) находим

Таким образом, в этом примере, как и следовало ожидать, скорость передачи информации оказалась равной пропускной способности канала: = C_c = 1/t.

Пример 2. Источник сообщений и способ их кодирования такие же, как и в примере 1, но вероятности сообщения при этом не одинаковы:

Р(х₁) = 0,5; Р(х₂) = 0,25; Р(х₃) = Р(х₄) = 0,125.

Для определения скорости передачи информации вновь воспользуемся формулой (1.2), для которой необходимо вычислить соответствующее значение энтропии Н(х) для источника разновероятных сообщений х₁, х_2, х₃, х₄ (n = 4):

Длительности всех сообщений остаются такими же, как и в примере 1:

t_с = 2t. Скорость передачи информации составит

 

В этом примере скорость передачи информации оказалась меньше пропускной способности двоичного канала C_с(0,875/t < 1/t).

Таким образом, отход от оптимальных статистических характеристик сигналов приводит к тому, что фактическая скорость передачи информации становится меньше пропускной способности канала. Этот вывод естественным образом следует из самого понятия о пропускной способности канала.

Пример 1 показывает, что фактическая скорость передачи информации может быть максимальной и равной пропускной способности канала, если статистические характеристики источника сообщений определенным образом согласованы со свойствами информационного канала. Для каждого источника сообщений это согласование может быть достигнуто специальным выбором способа кодирования и декодирования сообщений. Такое кодирование, при котором достигается наилучшее использование пропускной способности канала, называется эффективным.

К эффективным относится, в частности, код Шеннона - Фано, пригодный для кодирования статистически независимых сообщений.

Рассмотрим построение кода Шеннона - Фано для источника сообще-ний х₁, х_2, х₃, х₄, приведенных в примере 2. Использование равномерного кода для этих сообщений, как отмечалось ранее, не позволяет обеспечить максимальную скорость передачи информации. Покажем, что с помощью кода Шеннона - Фано рассматриваемые сообщения можно передать с мак-симальной скоростью, равной пропускной способности двоичного канала. Кодирование сообщений в этом случае иллюстрируется таблицей 1, которая составлена следующим образом.

Записывают сообщения в порядке убывания их вероятностей.

Проводят первое деление всех сообщений на две подгруппы I и II так, чтобы сумма вероятностей сообщений в подгруппах I и II была бы по возможности одинаковой. В данном случае это условие выполняется точно: при первом делении в подгруппу I входит сообщение х₁, вероятность которого равна 0,5, а в подгруппу II входят сообщения х₂, х₃, х₄, сумма вероятностей которых (0,25+0,125+0,125) будет тоже составлять 0,5.

Проводят второе аналогичное деление для каждой из полученных подгрупп сообщений. Процесс последовательных делений сообщений на подгруппы I и II прекращается в том случае, когда в подгруппе останется по одному сообщению.

Номер подгруппы, в которую попадает данное сообщение при каждом делении, определяет символ на соответствующей позиции кода этого сообщения. В рассматриваемой таблице принадлежность к подгруппе I обозначается символом 0, а к подгруппе II – символом 1. Так, в частности, первое деление дало на первой позиции кода для сообщения x₁ символ 0, а для остальных сообщений – символ 1.

Таблица 1

Сообще-ние xi	Вероят- ность р(хi)	Номер деления на подгруппы	Символ кода	Длительность кодовой комбинации ti
Позиции
х 1	0,5							1t
х2	0,25				2t
х3	0,125				3t
х4	0,125				3t

 

Как следует из таблицы 1, полученный код является неравномерным, т.е. сигналы разных сообщений имеют различное число символов, следовательно разную длительность. Для наглядности в таблице 2 для сообщений х ₁, х ₂, х ₃, х ₄ приведены неравномерный код Шеннона - Фано и равномерный, используемый ранее в примерах 1 и 2. Анализируя неравномерный код Шеннона - Фано, можно убедиться в том, что наиболее вероятному сообщению соответствует самая короткая кодовая комбинация, наименее вероятному – длинная. Этим можно объяснить увеличение скорости передачи информации при использовании данного кода.

Таблица 2

Сообщение x i	Код Шеннона - Фано	Равномерный код
x1
x2
x3
x4

 

Код Шеннона - Фано обладает еще одним существенным свойством: позволяет декодировать сообщения без введения дополнительных разделительных символов между кодовыми комбинациями, приводящих к снижению скорости передачи информации. Действительно, в рассмотренном примере короткие комбинации не совпадают с началом других более длинных кодовых комбинаций. Поэтому возможно однозначное декодирование последовательности кодовых комбинаций, формируемых непрерывно без применения разделительных символов. Коды, удовлетворяющие рассмотренному условию, называются префиксными кодами.

Для вычисления скорости передачи информации при использовании кода Шеннона - Фано воспользуемся формулой (1.2), применительно к которой, как и в примере 2, Н(Х) = 1,75, .

Как отмечалось выше, код Шеннона - Фано является неравномерным. Поэтому целесообразно отыскать среднюю длительность сигнала t_с одного сообщения, определяемую по формуле математического ожидания длительности t_i сообщения x_i [по аналогии с энтропией Н(Х)]:

.

Для выбранного примера по таблице 1 (n = 4) находим t_с = 1,75t, что позволяет считать кодовую комбинацию состоящей в среднем из m = 1,75 символов.

По формуле (1.2) для полученных значений Н(Х) и t_с находим скорость передачи:

.

Таким образом, в данном примере код Шеннона - Фано позволил полностью согласовать статистические характеристики источника сообщений с каналом связи, поскольку скорость передачи информации оказалась равной пропускной способности канала: .

Равномерный код, как отмечалось в примере 2, не является эффективным. Это можно объяснить тем, что при использовании эффективного кода Шеннона - Фано сигнал каждого сообщения в среднем состоит из 1,75 символов, а при использовании равномерного кода – из 2-х (таблица 2). Из чего следует, что в единицу времени сообщений, представленных кодом Шеннона - Фано, будет передано больше, чем при использовании равномерного кода.

Необходимо заметить и то, что, действуя по правилу построения кода Шеннона - Фано для четырех равновероятных сообщений, рассмотренных в примере 1, получаем приведенный в таблице 2 равномерный код, который в данном случае является эффективным.

Нарушение условия формирования кода Шеннона - Фано, заключа-ющегося в том, что наиболее вероятному сообщению должна соответствовать наиболее короткая кодовая комбинация, неизбежно приведет к снижению скорости передачи информации.

Для иллюстрации изложенного поменяем местами кодовые комбинации для сообщений х₁ и х₄ (см.табл.1). Тогда по формуле математического ожидания средняя длительность сообщения увеличится и составит , а скорость передачи информации

Использование рассмотренного эффективного кода согласуется с основной теоремой Шеннона для дискретного канала без помех. Теорема формулируется следующим образом: если поток информации , вырабатываемой источником, равен Н(Х) = С_с - x, где x - сколь угодно малая величина, то всегда можно найти такой способ кодирования, который обеспечивает передачу всех сообщений, вырабатываемых источником, причем скорость передачи = С_с - x.

Обратное утверждение состоит в том, что невозможно обеспечить передачу всех сообщений источника, у которого .

 

Пропускная способность дискретных каналов с шумами

 

Для дискретного канала с шумами (рис.1) количество информации, содержащейся в последовательности выходных сигналов z_T о входных сигналах Y_T, cоставит [2]

 

I(Z_T,Y_T) = H(Z_T) – H(Z_T|Y_T) = H(Y_T) – H(Y_T|Z_T), (1.5)

 

где H(Z_T|Y_T) и H(Y_T|Z_T) – условные энтропии.

Для последовательности сообщений длительностью Т, содержащей m сигналов источника, имеем

 

H(Z_T)= mH(Z), (1.6)

 

где H(Z) – энтропия выходного сигнала или энтропия выхода канала, рассматриваемого как эргодический источник.

Аналогично для условной энтропии выхода канала запишем

 

H(Z_T|Y_T) = mH(Z|Y). (1.7)

 

Тогда из (1.5)-(1.7) находим

I(Z_T,Y_T) = mH(Z) - mH(Z|Y). (1.8)

Скорость передачи в дискретном канале с шумами с учетом (1.8) составит

,(1.9)

где – средняя длительность сигнала одного сообщения.

 

Аналогично с учетом (1.5) найдем

. (1.10)

В равенстве (1.10) – поток информации на выходе кодирующего устройства, характеризует потерю информации, обусловленную действием помех.

Из соотношений (1.9) и (1.10) пропускная способность канала может быть определена из условия:

. (1.11)

В качестве примера рассмотрим двоичный канал связи без памяти. Каналами без памяти называются такие каналы, у которых на каждый передаваемый сигнал (символ) шум действует независимо от того, какие символы передавались ранее. Длительность передаваемых символов двоичного кода у₀ и у₁ («0» и «1») примем одинаковыми и равными t и, следовательно, t_с = t.

На выходе канала используется решающее устройство (РУ), с помощью которого принимаемые сигналы разделяются на две области z₀ и z₁ так, что если сигнал попадает в область z₀, то считается (принимается решение), что был передан сигнал y₀, а если в z₁, то – у₁.

Решающее устройство допускает принятие и ошибочных решений. Например, сигнал у₁ может быть искажен помехой так, что он оказывается в области z₀, в результате чего РУ принимает ошибочное решение, вероятность которого обозначим P(z₀½y₁) = P_I. Аналогичное ошибочное решение может быть принято и для сигнала у₀. Вероятность этого решения составит P(z₁½y₀) = P_II.

Очевидно, что при данных обозначениях вероятности правильного решения будут P(z₀½y₀) = 1 – P_II и P(z₁½y₁) = 1 - P_I. Для краткости записи обозначим априорные вероятности передачи сигналов P(y₀) = P₀ и P(y₁) = P₁ = 1 - P₀ . Для рассматриваемого двоичного канала введенные обозначения схематично показаны на рис. 2 в виде следующей модели.

 

 

 

Рис. 2. Модель двоичного канала

 

Используя правила теории вероятностей, можно найти значения априорных вероятностей различных решений, принимаемых на выходе канала:

(1.12)

Для вычисления пропускной способности рассматриваемого канала находим

 

 

или в принятых обозначениях вероятностей с учетом (1.12)

 

(1.14)

 

Подставив найденные значения и в формулу (1.9), получим соотношение, определяющее скорость передачи информации , из которого может быть найдено оптимальное значение априорной вероятности (Р_0опт) передачи сигнала у₀, при котором принимает максимальное значение, равное пропускной способности канала С _с.

Для иллюстрации изложенного рассмотрим в качестве примера симметричный двоичный канал без памяти. В этом канале P_I = P_II = P_ош, т.е. вероятности ошибочного приема сигналов (символов) у₀ и у₁ одинаковы. Тогда из (1.14) находим

.

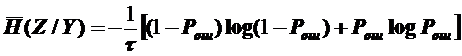Очевидно, не зависит от Р₀. В таком случае скорость передачи информации (1.9) будет максимальной, когда величина принимает наибольшее значение. Из свойств энтропии следует, что это условие выполняется, когда P(z₀) = P(z₁) = 0,5 и в этом случае .

Таким образом, для симметричного двоичного канала пропускная способность

. (1.15)

Как отмечалось выше, для достижения максимальной скорости передачи информации необходимо в кодирующем устройстве обеспечить такое формирование символов кода, при котором Р₀ = Р_0опт. Значение Р_0опт можно вычислить из выражений (1.12), приняв во внимание P_I = P_II = P_ош и P(z₀) = P(z₁). Путем вычитания из (1.12) находим

 

Р_0опт(1 – Р_ош) + (1 – Р_0опт)Р_ош – (1 – Р_0опт)(1 – Р_ош) – Р_0оптР_ош = 0.

 

Далее можем получить 1–2Р_0опт =2Р_ош(1–2Р_0опт), откуда Р_0опт= 0,5.

Таким образом, условие обеспечения максимальной скорости передачи информации в симметричном канале с шумами такое же, как и в канале без шумов. Однако наличие шумов, приводящих к ошибкам, снижает пропускную способность каналов.

На рис. 3 приведен график зависимости С_сt от Р_ош, полученный из формулы (1.15).

Pош

Рис. 3. График зависимости С_сt от Р_ош

Как видно из этого графика, при Р_ош = 0,5 пропускная способность канала С_с = 0. Этот результат станет очевидным, если учесть, что для значения Р_ош = 0,5 при передаче каждого из символов на выходе канала с равной вероятностью может быть принято решение z₀ и z₁. Эти решения могут иметь такую же ценность, как если бы передача сигналов прекратилась и на выходе канала принималось бы решение по результатам бросания монеты (цифра или герб). Интересно также отметить, что если Р_ош > 0,5, то с увеличением Р_ош пропускная способность канала возрастает. Этот, на первый взгляд, парадоксальный вывод становится очевидным, если принять во внимание, что мы всегда можем изменить правило распознавания символов на обратное, т.е. считать, что решение z₁ соответствует передаче символов у₀, а решение z₀ – передаче символа у₁. Тогда вероятность принятия ошибочного решения станет равной 1 – Р_ош.

 

Пропускная способность