Определение пропускной способности непрерывного канала

 

Рассмотрим случай, когда помеха в канале действует как аддитивный шум n(t), т.е.

z(t) = y(t) +n(t).

 

Допустим также, что этот шум – стационарный, имеет нормальный закон распределения и его средняя мощность равна его дисперсии P_ш=s_N² (s_N² – дисперсия сигнала помехи). Заметим, что шум с нормальным законом распределения обладает максимальной энтропией и, следовательно, такой шум создает максимальное воздействие на полезный сигнал.

Определив пропускную способность канала, примем во внимание, что его полоса частот пропускания ограничена пределами от 0 до F_m, а средняя мощность Р_c полезного сигнала y(t) выражается через его дисперсию: P_c = =s _Y².

С учетом ограничения полосы частот пропускания канала спектры частот сигналов y(t), z(t) и n(t) не должны превышать частоты F_m. В этом случае и тогда выражение (2.5) можно представить так:

 

.

 

В случае аддитивной помехи последнее выражение можно записать как

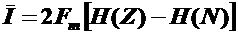, (2.9)

 

где H(N) – энтропия источника помехи в нашем случае с нормальным законом распределения, имеющим вид

. (2.10)

Энтропию такого источника найдем по формуле

 

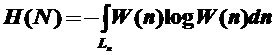. (2.11)

Так как и , из выражения (2.11) с учетом (2.10) получим

Пропускную способность рассматриваемого канала можно найти с учетом (2.9) и (2.12) в виде

 

. (2.13)

 

Поскольку F_m и s_N в нашем случае заданы, то выражение, стоящее в квадратных скобках, будет наибольшим, если энтропия выходных сигналов канала H(Z) будет максимальной. Так как средние мощности полезного сигнала y(t) и шума n(t) ограничены, то их аддитивная смесь на выходе канала z(t) будет также иметь ограниченную мощность. При таком условии известно, что H(Z) будет наибольшей, если z(t) имеет нормальный закон распределения. Поскольку помеха имеет нормальный закон распределения, то и полезный сигнал y(t) должен иметь нормальный закон распределения. Если полезный сигнал и сигнал помехи статистически независимы, то s_Z² = s_Y² + s_N² и, следовательно,

.

Подставляя это значение H(Z) в (2.13) и учитывая обозначения s _Y²= Р_с и s_N² = Р_ш, получаем

. (2.14)

Выражение (2.14) представляет собой широко известную формулу Шеннона. Учитывая важность формулы Шеннона, проводим ее более детальное обсуждение. Из равенства (2.14) следует, что увеличить пропускную способность непрерывного канала можно или за счет расширения его полосы частот пропускания F_m и соответствующего расширения спектра полезного сигнала, или за счет увеличения мощности полезного сигнала Р_с.

Из рассмотрения формулы (2.14) следует, что одно и то же значение пропускной способности можно получить при разных комбинациях значений полосы частот пропускания канала и отношения Р_с /Р_ш.

Рассмотрим два канала: один с полосой частот пропускания от 0 до W₀ (W₀= F_м), а другой – от 0 до W > W₀. При одинаковых пропускных способностях для первого канала отношение мощностей сигнал/шум составит (Р_с /Р_ш)₀, а для второго – Р_с /Р_ш.

С учетом выражения (2.14) и введенных обозначений для рассматриваемых каналов получим

 

,

 

откуда находим

 

. (2.15)

 

Считая, что шум имеет равномерную спектральную плотность, мощность напряжения шума в полосе частот пропускания первого канала составит Р_ш = S₀W₀, а второго – Р_ш = S₀W. Здесь S₀ характеризует мощность шума в полосе 1 Гц. Тогда выражение (2.15) можно представить в виде

 

.

 

На выходе реальных каналов . Тогда из (2.15) находим отношение эффективных значений напряжений сигнала и шума:

 

, (2.16)

 

где .

, (2.17)

значение h² представляет отношение мощности сигнала к удвоенной мощности шума в полосе частот пропускания канала W₀ или требуемое отношение средней энергии сигнала, связанной с одним отсчетом непрерывного сигнала с максимальной частотой спектра W₀, к спектральной плотности шума S₀.

Рассмотрим случай, когда W®¥. Тогда из (2.16) получим

. (2.18)

 

Из (2.18) следует, что минимально возможная требуемая мощность сигнала в идеальном канале с полосой частот пропускания W₀ определится как

. (2.19)

Для заданной конечной полосы частот пропускания непрерывного канала W минимально возможная величина h_мин² может быть определена из выражения (2.17) как

. (2.20)

Выше отмечалось, что условие максимальной скорости передачи информации обеспечивается в случае, когда источник сообщения имеет нормальный закон распределения. Реальные источники обычно имеют ограниченный диапазон изменения непрерывной случайной величины от

-u_c до +u_c.. Наибольшее значение энтропии таких источников дает равномерное распределение. При одинаковой информативности эффективное напряжение источника с равномерным распределением, равное , должно несколько увеличиваться (не более 20% по сравнению с источником с нормальным распределением).

В реальных каналах обычно в целях простоты рассматривается прохождение гармонических сигналов с амплитудой u_c. Эффективное напряжение гармонического (синусоидального) сигнала составляет 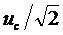. Тогда перерасчет отношения с/ш для гармонического сигнала и сигнала с равномерным распределением будет иметь вид

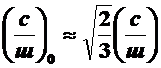. (2.21)

Заметим, что через отношение выражается относительная шумовая среднеквадратическая погрешность на выходе каналов:

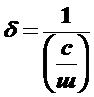. (2.22)

Принимая d = 0,01 ( = 100) и используя формулы (2.21) и (2.22), находим , а по формуле (2.19) –

h²_{мин мин} = ln 81,6 = 4,4.

На рис. 5 по формуле (2.19) построена зависимость для случая d = 0,01.

Рис. 5. Зависимости для идеального канала

и реальных каналов с АМ и ЧМ

 

Известно, что в канале с тональной (гармонической) амплитудной модуляцией (АМ)

,

или с учетом (2.17)

. (2.23)

С учетом ширины частотного спектра сигнала в канале при АМ [3] имеем . Если из формулы (2.23) для d_АМ = 0,01 находим h² = 10⁴. Если увеличивать полосу канала, выбирая W > 2W₀, то мощность шума будет пропорционально возрастать и для сохранения шумовой погрешности d_АМ=0,01 необходимо соответственно увеличивать мощность полезного сигнала, а следовательно, и значение h², т.е. зависимость будет линейной (рис. 5). Таким образом, увеличение полосы частот пропускания канала с АМ, в отличие от идеального канала, приводит к ухудшению его энергетических показателей. Поэтому в канале с АМ совершенно нецелесообразно выбирать .

Для канала с частотной модуляцией (ЧМ)

 

(2.24)

 

где - индекс ЧМ,

- наибольшее отклонение частоты при тональной ЧМ,

.

 

Полоса частот пропускания канала с ЧМ по формулам Манаева определяется как

(2.25)

или

. (2.26)

С учетом (2.25) находим

 

 

и тогда формула (2.24) примет вид

 

. (2.27)

 

Обычно при ЧМ стараются для снижения шумовой погрешности (2.24) выбирать D >> 1. В этом случае (2.24) примет вид

 

. (2.28)

 

Из формулы (2.28) следует, что с увеличением полосы частот пропускания канала W шумовая погрешность d_ЧМ будет уменьшаться.

Это свойство канала с ЧМ легко объясняется. При увеличении полосы частот пропускания канала для согласования частотного спектра сигнала необходимо повысить индекс ЧМ D [см. формулу (2.26)], а увеличение D приводит к уменьшению шумовой погрешности d_ЧМ [см. формулу (2.24)].

При заданной погрешности d_ЧМ увеличение полосы частот пропускания канала позволяет уменьшить значение h [см. формулу (2.27)], т.е. снизить значение эффективного напряжения полезного сигнала на входе канала.

Из сопоставления формул (2.23) и (2.24) при малых значениях канал с ЧМ не имеет преимуществ по шумовой погрешности по сравнению с АМ. Заметим, что при малых значениях D полосы частот пропускания каналов с ЧМ и АМ практически одинаковы. На рис. 5 качественно приведена зависимость для канала с ЧМ, из которой видно, что в канале с ЧМ более рационально используется расширение полосы частот пропускания, чем в канале с АМ. Однако канал с ЧМ существенно уступает идеальному каналу по Шеннону, особенно при значениях W/W₀ > (W/W₀)_опт, когда очень резко появляются так называемые аномальные выбросы шумов. Поэтому при ЧМ оптимальную величину индекса модуляции D и минимальную величину h² выбирают при W_опт [3]. Более выгодное использование полосы частот пропускания, аналогичное идеальному каналу, обеспечивается в реальных каналах с кодоимпульсной модуляцией (КИМ) и широкополосными сигналами (ШПС).

 

Методические указания

 

Для изучения данного пособия необходимо предварительно усвоить количественные меры информации для дискретных (цифровых) и непрерывных (аналоговых) источников [1]: мера Хартли, энтропия, условная энтропия, количественная мера информации при неполной достоверности сообщений и их свойства.

Для контроля самостоятельного усвоения составлены вопросы для самопроверки.

Материал пособия может быть использован при выполнении курсового проекта, требования к которому и его особенности излагаются в лекционном материале (10 часов) и на практических занятиях (8 часов) в 6-м семестре.

4. Контрольные вопросы для самопроверки

 

Раздел 1

 

4.1.1. Дайте определение энтропии источника дискретных (цифровых) сообщений.

4.1.2. Перечислите свойства энтропии.

4.1.3. Дайте определение условной энтропии.

4.1.4. Запишите выражение для определения количества информации при неполной достоверности получаемых сообщений.

4.1.5. Как определяется энтропия источника непрерывных (аналоговых) сообщений?

4.1.6. Как определяется условная энтропия непрерывных (аналоговых) источников?

4.1.7. Как определяется скорость передачи информации?

4.1.8. От каких факторов зависит скорость передачи информации в дискретных (цифровых) и непрерывных (аналоговых) каналах?

4.1.9. Дайте определение пропускной способности непрерывных и дискретных каналов.

4.1.10. Что такое дискретный канал без помех?

4.1.11. Какое кодирование называется эффективным?

4.1.12. Как построить код Шеннона - Фано?

4.1.13. Как доказать, что код Шеннона - Фано может быть эффективным?

4.1.14. Чем отличается равномерный код от неравномерного?

4.1.15. Почему код Шеннона - Фано можно декодировать без введения дополнительных разделительных символов?

4.1.16. Чем можно объяснить (без формул) увеличение скорости передачи информации при использовании эффективного кода Шеннона-Фано?

4.1.17. В каком случае двоичный равномерный код может быть эффективным?

4.1.18. В каких случаях код Шеннона - Фано становится неэффективным?

4.1.19. Что такое поток информации?

4.1.20. Сформулируйте теорему Шеннона для канала без помех.

4.1.21. Что такое дискретный канал с шумами?

4.1.22. Как определяются скорость передачи информации в дискретном канале с шумами и его пропускная способность?

4.1.23. Что такое двоичный канал без памяти?

4.1.24. Какие функции выполняет решающее устройство в двоичном канале с шумами?

4.1.25. Может ли решающее устройство принимать ошибочные решения?

4.1.26. Как определяется скорость передачи информации и пропускная способность двоичного симметричного канала без памяти?

4.1.27. Как изменяется пропускная способность двоичного симметричного канала без памяти в зависимости от вероятности ошибки в канале? Приведите график этой зависимости.

4.1.28. Каково условие обеспечения максимальной скорости передачи в симметричном канале с шумами?

4.1.29. Чем объясняется снижение скорости передачи информации и пропускной способности двоичного канала с шумами по сравнению с двоичным каналом без помех?

 

Раздел 2

 

4.2.1. Приведите структуру непрерывного (аналогового) канала.

4.2.2. Как определяется скорость передачи информации в непрерывном канале?

4.2.3. Как определяется пропускная способность непрерывного канала?

4.2.4. Как вычисляется энтропия источника непрерывного сообщения с нормальным законом распределения?

4.2.5. Приведите формулу Шеннона для непрерывного канала.

4.2.6. От чего зависит пропускная способность непрерывного канала?

4.2.7. Почему в идеальном канале по Шеннону при увеличении его полосы частот пропускания требуемая мощность полезного сигнала уменьшается?

4.2.8. Какова ширина спектра частот при тональной АМ?

4.2.9. Как выбирается минимальная полоса частот пропускания в канале с АМ?

4.2.10. Как находится шумовая среднеквадратическая погрешность в канале с АМ?

4.2.11. Почему полосу частот пропускания канала с АМ нецелесообразно увеличивать относительно минимального значения?

4.2.12. Как находится полоса частот пропускания канала с ЧМ?

4.2.13. Как определяется шумовая среднеквадратическая погрешность в канале с ЧМ?

4.2.14. Почему полосу частот пропускания канала с ЧМ, в отличие от АМ, можно увеличивать?

4.2.15. Дайте сравнительную оценку реальных каналов с АМ и ЧМ и идеального канала по Шеннону по использованию их полосы частот пропускания.

4.2.16. Какие реальные каналы приближаются к идеальному каналу по Шеннону?