КИНЕМАТИКА ТОЧКИ
Содержание: задачи кинематики; траектория, скорость, ускорение точки. Векторный способ задания движения точки. Векторы скорости и ускорения точки (годограф скорости). Примеры. Скорость и ускорение точки в полярных координатах. Координатный способ задания движения. Определение скорости и ускорения точек по их проекциям на координатные оси.
Основные понятия, задачи кинематики
Задачи кинематики состоят в определении способов задания движения материальной точки, твердого тела и механической системы, также методов вычисления скорости и ускорения точки (или точек твердого тела, механической системы).
Задать движение материальной точки или твердого тела (точек механической системы) - это значит задать способ вычисления положения точки или течек твердого тела (точек механической системы) в любой момент времени.
Траектория точки. Геометрическое место последовательных положений движущейся точки в декартовой системе координат 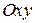 называется траекторией. Если в интервале времени
называется траекторией. Если в интервале времени  траектория прямая линия, то движение в этом интервале называется прямолинейным, в противном случае – движение называется криволинейным (рис. 2.1).
траектория прямая линия, то движение в этом интервале называется прямолинейным, в противном случае – движение называется криволинейным (рис. 2.1).

Рис. 2.1
В частности, движение точки на интервале времени  называют круговым, если на этом интервале точка движется по окружности.
называют круговым, если на этом интервале точка движется по окружности.
Скорость точки. Пусть положение движущейся точки М относительно произвольно выбранного неподвижного центра О определяется в момент
| а | 
| времени t радиус– вектором 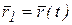 , который соединяет движущуюся точку М с центром О, (рис. 2.2, а). В следующий момент времени , который соединяет движущуюся точку М с центром О, (рис. 2.2, а). В следующий момент времени 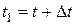 положение точки (точка М1) определяется радиус–вектором положение точки (точка М1) определяется радиус–вектором 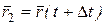 . За время . За время  , радиус-вектор изменится на , радиус-вектор изменится на
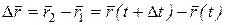 .
Средней скоростью .
Средней скоростью 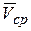 точки за время точки за время 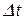 называют соотношение называют соотношение 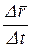 , т.е. , т.е.
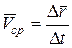 (2.1) (2.1)
|
| б | 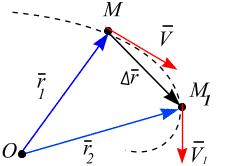 Рис. 2.2
Рис. 2.2
|
Средняя скорость параллельна вектору  и не имеет точки приложения (рис. 2.2, а).
и не имеет точки приложения (рис. 2.2, а).
Мгновенная скорость точки  в момент времени t определяется как предел средней скорости при Δt → 0, т.е.
в момент времени t определяется как предел средней скорости при Δt → 0, т.е.
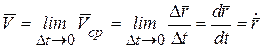 . (2.2)
. (2.2)
Производная по времени от функций обозначается точкой над символом этой функции, а вторая производная – двумя точками.
Вектор скорости приложен в точке М, направлен в сторону ее движения по предельному направлению вектора  → 0, т.е. совпадает с касательной к траектории в точке М (рис. 2.2, б ). Размерность скорости в СИ:
→ 0, т.е. совпадает с касательной к траектории в точке М (рис. 2.2, б ). Размерность скорости в СИ:  = длина/время = м/с. Часто скорость выражают в км/ч = 0,28 м/с.
= длина/время = м/с. Часто скорость выражают в км/ч = 0,28 м/с.
| Скорость - это векторная величина, характеризующая быстроту и направление движения точки |
Ускорение точки. Пусть движущаяся точка М в момент времени t имеет скорость  (рис. 2.2). В момент времени
(рис. 2.2). В момент времени 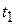 = t + Δt эта точка занимает положение М1, имея скорость
= t + Δt эта точка занимает положение М1, имея скорость 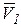 . Чтобы изобразить приращение скорости
. Чтобы изобразить приращение скорости  за время Δt, перенесем вектор скорости
за время Δt, перенесем вектор скорости 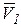 параллельно самому себе в точку М, тогда
параллельно самому себе в точку М, тогда 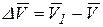 .
.
| а | 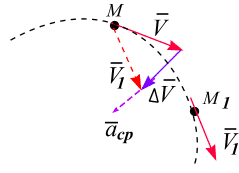
| Средним ускорением точки  за время Δt называется отношение за время Δt называется отношение  , т.е. , т.е.
 . (2.3)
Вектор . (2.3)
Вектор 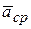 совпадает с направлением вектора совпадает с направлением вектора  , т.е направлен внутрь вогнутости траектории (рис. 2.3, а).
Ускорением точки , т.е направлен внутрь вогнутости траектории (рис. 2.3, а).
Ускорением точки 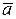 в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т.е. в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т.е.
 . (2.4) . (2.4)
|
| б | 
| |
| Рис. 2. 3 |
Вектор ускорения 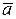 всегда направлен внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.3, 6). Размерность ускорения в СИ:
всегда направлен внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.3, 6). Размерность ускорения в СИ: 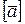 = длина/время2 = м/с2.
= длина/время2 = м/с2.
| Ускорение – векторная величина, которая характеризует быстроту изменения модуля и направления вектора скорости. |
Вопрос о скорости был “камнем преткновения” до начала ньютоновской эпохи в механике. Задачи на вычисление скорости движения какого-либо тела тогда были неразрешимы. Кроме того, существовали многочисленные «парадоксы». Один из них придуман Зеноном, он хорошо показывает, насколько была сложна до Ньютона проблема вычисления и определения скорости движения. Зенон – греческий философ и астроном, живший на о. Кипр около 336-264 до н.э., известный еще и тем, что одним из первых правильно объяснил затмение солнца и луны.
 «Предположим, – говорил он, – что Ахиллес (рис. 2.3, точка
«Предположим, – говорил он, – что Ахиллес (рис. 2.3, точка 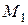 ) бегает в десять раз быстрее черепахи (рис. 2.4, точка
) бегает в десять раз быстрее черепахи (рис. 2.4, точка  ). Тем не менее, Ахиллес никогда не перегонит черепаху. Действительно, пусть в начале состязания черепаха находилась в 100 метрах впереди Ахиллеса
). Тем не менее, Ахиллес никогда не перегонит черепаху. Действительно, пусть в начале состязания черепаха находилась в 100 метрах впереди Ахиллеса 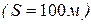 . Тогда ко времени, когда Ахиллес пробежит эти 100 метров, черепаха окажется в 10 метрах впереди него. Пробежав и эти 10 метров, Ахиллес увидит черепаху в 1-ом метре впереди себя. За то время, пока он пробежит этот метр, черепаха пройдет 10 сантиметров и т.д. до бесконечности. Следовательно, в любой момент черепаха будет впереди Ахиллеса, и он когда не сможет перегнать».
. Тогда ко времени, когда Ахиллес пробежит эти 100 метров, черепаха окажется в 10 метрах впереди него. Пробежав и эти 10 метров, Ахиллес увидит черепаху в 1-ом метре впереди себя. За то время, пока он пробежит этот метр, черепаха пройдет 10 сантиметров и т.д. до бесконечности. Следовательно, в любой момент черепаха будет впереди Ахиллеса, и он когда не сможет перегнать».
Для разрешения этого парадокса была высказана новая идея независимо Ньютоном и Лейбницем, которая положила начало новой области математики, помимо хорошо изученных учеными в те времена геометрии и алгебры. Для описания движения Ньютон ввел параметр 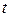 , назвал его абсолютным временем и стал рассматривать путь, пройденный Ахиллесом и черепахой в единицу времени, т.е. рассматривать движение в плоскости с координатами
, назвал его абсолютным временем и стал рассматривать путь, пройденный Ахиллесом и черепахой в единицу времени, т.е. рассматривать движение в плоскости с координатами 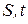 (рис. 2.4). За одно и тоже время
(рис. 2.4). За одно и тоже время 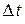 Ахиллес пройдет путь
Ахиллес пройдет путь 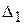 (точка
(точка 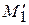 ), а черепаха
), а черепаха 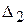 (точка
(точка 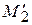 ), причем
), причем 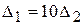 . Соединяя полученные точки (
. Соединяя полученные точки (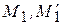 ) и (
) и (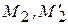 ) в плоскости (
) в плоскости (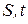 ), получим две прямые под разными углами к оси t. Очевидно, что если угол наклона прямой (1) – угол
), получим две прямые под разными углами к оси t. Очевидно, что если угол наклона прямой (1) – угол 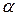 , будет больше угла наклона кривой (2) – угол
, будет больше угла наклона кривой (2) – угол  , то Ахиллес перегонит черепаху в момент времени
, то Ахиллес перегонит черепаху в момент времени 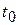 , когда прямые (1) и (2) пересекутся.
, когда прямые (1) и (2) пересекутся.
Новая идея заключалась в том, чтобы малые расстояния (путь  ) рассматривать на соответствующих малых отрезках времени
) рассматривать на соответствующих малых отрезках времени 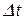 и посмотреть, что произойдет с частным, если отрезок времени
и посмотреть, что произойдет с частным, если отрезок времени 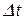 брать все меньше и меньше. Иными словами, брать предел отношения пройденного расстояния
брать все меньше и меньше. Иными словами, брать предел отношения пройденного расстояния  к интервалу времени при неограниченном уменьшении последнего. Тогда, скорость движения Ахиллеса
к интервалу времени при неограниченном уменьшении последнего. Тогда, скорость движения Ахиллеса 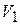 и скорость движения черепахи
и скорость движения черепахи 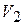 определятся через углы наклона прямых
определятся через углы наклона прямых 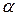 и
и  (рис. 2.4) следующим образом
(рис. 2.4) следующим образом

|  .
Путь .
Путь  , пройденный точкой, зависит от времени, следовательно, является функцией времени, т.е. , пройденный точкой, зависит от времени, следовательно, является функцией времени, т.е.  . Предел . Предел 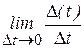 был назван производной от функции был назван производной от функции 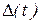 . Исаак Ньютон (Newton, Isaac) (1643-1727) и Лейбниц Готфрид Вильгельм (Leibniz, Gottfried Wilhelm von) (1646–1716), заложили основы новой области математики – дифференциального и интегрального исчисления. . Исаак Ньютон (Newton, Isaac) (1643-1727) и Лейбниц Готфрид Вильгельм (Leibniz, Gottfried Wilhelm von) (1646–1716), заложили основы новой области математики – дифференциального и интегрального исчисления.
|
| Исаак Ньютон | |

| |
| Г. В. Лейбниц |
§ 2. 2. Векторный способ задания движения точки* [1]
Движение точки задается радиус– вектором 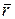 этой точки. Движение точки считается заданным, если известен радиус – вектор движущейся точки как функция времени, т.е.
этой точки. Движение точки считается заданным, если известен радиус – вектор движущейся точки как функция времени, т.е.
 . (2.5)
. (2.5)
 Рис. 2.5
Рис. 2.5
|
Уравнение (2.5) называется уравнением движения точки, заданное векторным способом. Заданное уравнение движения полностью определяет движение точки.
Пусть 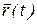 задает движение точки М, тогда при изменении t точка опишет кривую в пространстве (рис. 2.5). Эта кривая называется годографом радиус-вектора и соответствует траектории точки.
задает движение точки М, тогда при изменении t точка опишет кривую в пространстве (рис. 2.5). Эта кривая называется годографом радиус-вектора и соответствует траектории точки.
Вектор скорости направлен по касательной к траектории в точке  –
–  (рис. 2.4) и вычисляется по формуле
(рис. 2.4) и вычисляется по формуле
 . (2.6)
. (2.6)
Вектор ускорения направлен внутрь вогнутости траектории в точке  и вычисляется по формуле:
и вычисляется по формуле:
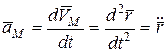 . (2.7)
. (2.7)
Покажем технологию вычисления скорости и ускорения точки А.
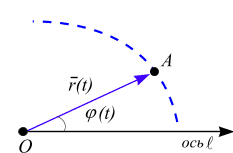
Пусть движение точки А происходит в заданной плоскости. Зададим радиус – вектор движущейся точки как функция времени т.е. зададим функции 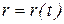 ,
,  , рис.2.6, а
, рис.2.6, а
а
| б | 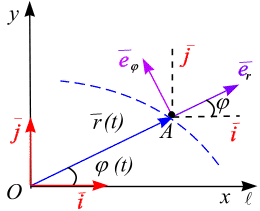
|
Рис. 2.6
Совместим начало декартовой системы координат и ось 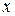 с полюсом
с полюсом 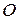 и полярной осью
и полярной осью 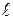 , соответственно (рис. 2.6, б). Радиус – вектор
, соответственно (рис. 2.6, б). Радиус – вектор  разложим по единичным ортам
разложим по единичным ортам 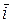 ,
,  :
:
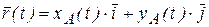 .
.
Введем  - единичный вектор, направленный вдоль радиус-вектора
- единичный вектор, направленный вдоль радиус-вектора  в сторону возрастания модуля
в сторону возрастания модуля  , и
, и 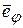 - единичный вектор, получающийся из
- единичный вектор, получающийся из 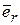 поворотом последнего на угол
поворотом последнего на угол 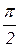 против часовой стрелки. Единичные векторы
против часовой стрелки. Единичные векторы 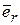 и
и  задают направления двух взаимно перпендикулярных осей. Ось, направление которой определено единичным вектором
задают направления двух взаимно перпендикулярных осей. Ось, направление которой определено единичным вектором  называется радиальной, а единичным вектором
называется радиальной, а единичным вектором 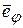 – трансверсальной. В системе координат Оху векторы
– трансверсальной. В системе координат Оху векторы  и
и  можно связать с единичными ортами
можно связать с единичными ортами 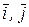 следующим образом (рис.2.6, б):
следующим образом (рис.2.6, б):
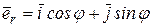 ,
,
 .
.
Вычислим скорость точки А. Так как
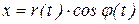 ,
, 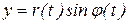 ,
,
имеем

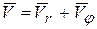 .
.
Модуль скорости
 . (2.8)
. (2.8)
Проекции скорости  на радиальную ось -
на радиальную ось - 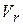 и трансверсальную ось -
и трансверсальную ось - 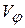 и называются соответственно радиальной и трансверсальной скоростями.
и называются соответственно радиальной и трансверсальной скоростями.
Угол, образованный вектором скорости с положительным радиальным направлением, вычисляется по формуле
 .
.
Для ускорения 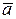 аналогично получаем:
аналогично получаем:
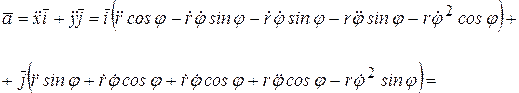

 .
.
Тогда модуль ускорения
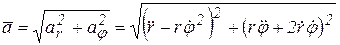 ,. (2.9)
,. (2.9)
Проекции ускорения 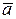 на радиальную ось -
на радиальную ось -  и трансверсальную ось -
и трансверсальную ось -  называются радиальным и трансверсальным ускорениями соответственно. Угол, образованный вектором ускорения с положительным радиальным направлением, вычисляется по формуле
называются радиальным и трансверсальным ускорениями соответственно. Угол, образованный вектором ускорения с положительным радиальным направлением, вычисляется по формуле
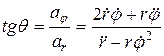 .
.
Движение задано радиус-вектором  , тогда , тогда
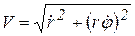 , , 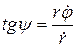 ; ;
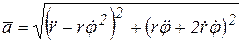 , , 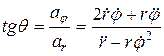 . .
|
Пример 2.1. Движение точки задано радиус-вектором 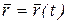 :
:
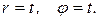 (а)
(а)
Построить траекторию, вычислить скорость и ускорение точки для моментов времени 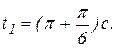 ,
, 
Решение. Исключая из уравнений движения (а) параметр t, получим уравнение траектории в полярных координатах: r=j. Это уравнение описывает движение точки А по лучу 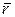 , вращающемуся около полюса О. Траектория такого движения называется спиралью Архимеда (рис. 2.7).
, вращающемуся около полюса О. Траектория такого движения называется спиралью Архимеда (рис. 2.7).

Рис. 2.7
Точка при 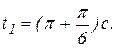 занимает положение
занимает положение 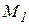 с координатами:
с координатами: 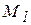 (
( ).
).
Точка при  занимает положение
занимает положение  с координатами:
с координатами: 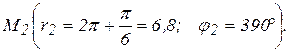
Проекции скорости и ускорений на полярные оси вычислим по формулам:
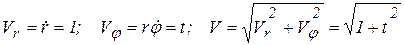 ;
;
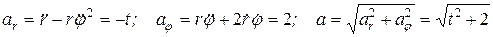 .
.
Вычислим скорость и ускорение точки при 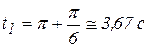 :
:
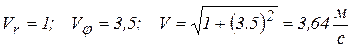 ;
;
 .
.
Вычислим скорость и ускорение точки при 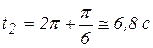 :
:
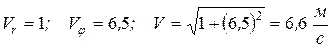 ;
;
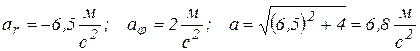 .
.
Пример 2.2. Движение точки задано в уравнением
 .
.
Построить траекторию движущейся точки и вычислить ее скорость при 
Решение. Построить траекторию движущейся точки – это значит построить годограф радиус – вектора. Для построения годографа составим таблицу 2.1 точек годографа для отдельных значений t.
Табл. 2.1
| t | 0 | 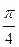
| 
| 
| 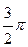
| 
|

| 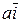
| 
| 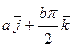
| 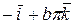
| 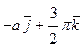
| 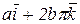
|
Для любой точки годографа имеем:  ,
, 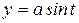 ,
, 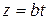 , поэтому при любом t выполняется равенство х2+у2=а2, т.е. все точки годографа лежат на цилиндре, направляющей которого является окружность в плоскости переменных х, у, а образующая параллельна оси
, поэтому при любом t выполняется равенство х2+у2=а2, т.е. все точки годографа лежат на цилиндре, направляющей которого является окружность в плоскости переменных х, у, а образующая параллельна оси 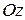 . Искомый годограф имеет вид, изображенный на рис. 2.8 a, и называется винтовой линией.
. Искомый годограф имеет вид, изображенный на рис. 2.8 a, и называется винтовой линией.
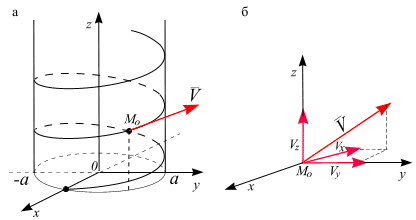
Рис. 2.8
Вычислим положение точки при заданном времени.
Точка МО при  имеет координаты:
имеет координаты: 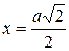 ,
,  ,
, 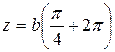 .
.
Вычислим скорость точки для текущего времени:
 .
.
При 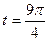 , рис. 2.8, б:
, рис. 2.8, б:
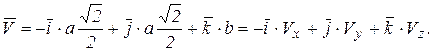
Координатный способ задания движения точки
Рассмотрим движение точки в плоскости. Пусть Оху – неподвижная декартова система координат.Можно задать значения координат движущейся точки для каждого момента, т. е. задать зависимости
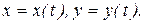 (2.10)
(2.10)
Уравнения (2.10) представляют собой уравнения движения точки в декартовых прямоугольных координатах.
Зная уравнения (2.10), можно вычислить для каждого момента времени соответствующие значения x, y и, следовательно, указать положение точки по отношению к выбранной системе Оxy. Поэтому уравнения (2.10) являются также и уравнениями траектории точки, заданными параметрически. Для получения явного вида уравнения траектории, т.е. зависимости 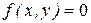 , следует из уравнений (2.10) исключить параметр t.
, следует из уравнений (2.10) исключить параметр t.
Радиус – вектор  , если заданы функции (2.10), имеет вид (рис. 2.9)
, если заданы функции (2.10), имеет вид (рис. 2.9)
 ,
,
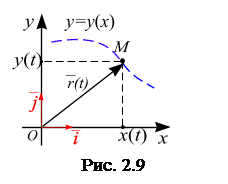 где
где 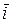 ,
,  – единичные орты системы координат Оxy.
– единичные орты системы координат Оxy.
Вектор скорости вычисляется, как производная от  по времени, т.е.
по времени, т.е.
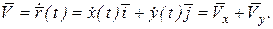
Модуль вектора скорости вычисляется так
 , (2.11)
, (2.11)
здесь 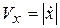 ,
, 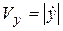 – проекции скорости
– проекции скорости  на оси
на оси 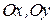 , знак производных
, знак производных 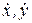 показывает направление проекций скорости по отношению к соответствующим осям
показывает направление проекций скорости по отношению к соответствующим осям 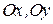 соответственно.
соответственно.
Направление вектора скорости вычисляется по направляющим косинусам:
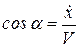 . (2.11,а)
. (2.11,а)
Вектор ускорения вычисляется, как вторая производная от 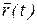 по времени, т.е.
по времени, т.е.
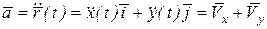 .
.
Для вычисления модуля ускорения, имеем
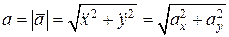 , (2.12)
, (2.12)
где  ,
, 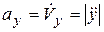 – проекции вектора
– проекции вектора 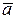 на оси
на оси 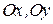 соответственно, знак производных
соответственно, знак производных 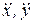 показывает направление проекций ускорения по отношению к осям
показывает направление проекций ускорения по отношению к осям 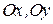 .
.
Направление вектора ускорения вычисляется по направляющим косинусам
 . (2.12,а)
. (2.12,а)
Рассмотрим движение точки в плоскости. Тогда, уравнения движения точки в декартовых координатах Оху имеют вид:
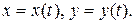 (2.13)
(2.13)
Уравнения (2.9) являются также уравнениями траектории точки, заданными параметрически, т. е. в системах координат 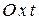 и
и 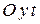 .
.
Уравнение траектории в явном виде, т. е. в системе координат 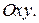 .Для получения этой зависимости, следует из уравнений (2.13) исключить параметр
.Для получения этой зависимости, следует из уравнений (2.13) исключить параметр 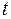 .Уравнение траектории в явном виде будет иметь вид функции
.Уравнение траектории в явном виде будет иметь вид функции  .
.
Например, заданы уравнения движения точки:
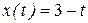 ,
, 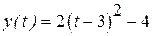 ,
,
в явном виде уравнение движения точки будет иметь вид

Скорость и ускорение точки по модулю и направлению вычисляются по формулам:
 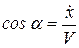 ; ;
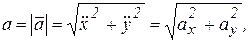 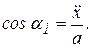
| |||
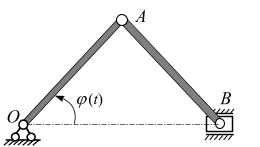 Рис. 2.10
Рис. 2.10
| Пример 2.3. Положение кривошипа ОА в кривошипно-ползунном механизме (рис. 2.10) определяется углом  (рад). Вычислить скорость и ускорение точек А и В в моменты (рад). Вычислить скорость и ускорение точек А и В в моменты 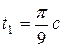 если если 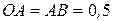 м. м.
| ||
Решение. Декартовую систему координат 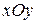 совместим с точкой О кривошипа 0А (рис. 2.11).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты -
совместим с точкой О кривошипа 0А (рис. 2.11).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты -  и
и 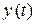 каждой точки.
каждой точки.
Вычислим положение механизма при 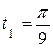 с, которое определяется углом
с, которое определяется углом 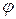 . Имеем:
. Имеем:
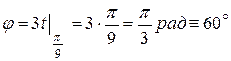 .
.
Точка А движется по окружности, радиус которой равен длине кривошипа ОА, точка В – прямолинейно вдоль оси 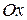 . Следовательно, в любой момент времени положение точки А определяется координатами
. Следовательно, в любой момент времени положение точки А определяется координатами 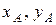 , а движение точки В определяться координатой
, а движение точки В определяться координатой 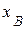 (рис. 2.11).
(рис. 2.11).
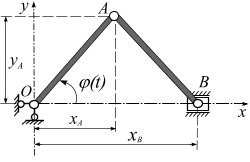 Рис. 2.11 Рис. 2.11
| Имеем:
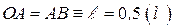 ; ;
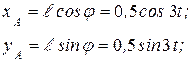
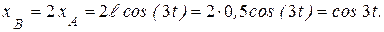
|
Скорость и ускорения точки А (рис. 1.3, а):
Скорость точки А:
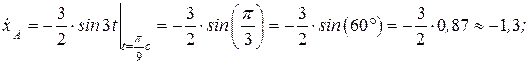
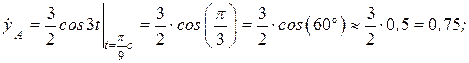
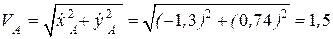 (м/c).
(м/c).
| а | 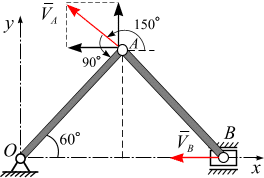
| б | б
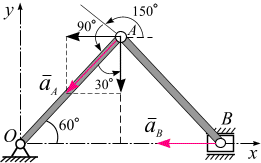
| |
| Рис. 2.12 |
Направление вектора скорости:
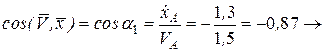
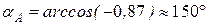 .
.
Ускорение точки А (рис. 2.12, б):

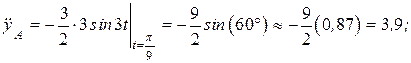
 (м/c).
(м/c).
Имеем:

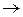 точка А вдоль оси
точка А вдоль оси 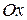 движется ускоренно;
движется ускоренно;
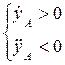
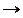 точка А вдоль оси
точка А вдоль оси 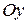 движется замедленно.
движется замедленно.
Направление вектора ускорения:
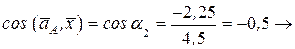
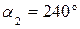 .
.
Скорость точки и ускорение В (рис. 2.12, а, б)
 м/c;
м/c;
 м/c2
м/c2
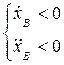
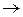 точка В движется против оси
точка В движется против оси 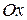 ускоренно.
ускоренно.
Пример 2.4. Движение точки M по плоскости Оху задано уравнениями движения
 . (а)
. (а)
Построить траекторию движущейся точки, вычислить скорость и ускорение точки в моменты времени  и
и 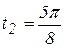 .
.
Решение. Дляпостроения траектории движущейся точки в декартовой системе координат определим область, в которой движется точка, т.е. область значений  и
и 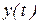 .[2] Функции
.[2] Функции 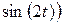 и
и 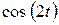 - ограничены, т.е.
- ограничены, т.е.  ,
,  , получаем:
, получаем:
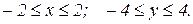
Выделяем на координатной плоскости область, ограниченную полученными неравенствами, за эту область точка при движении не выходит
(рис. 2.10). Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:
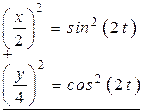
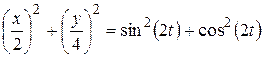 .
.
 Рис. 2.13 Рис. 2.13
| Учитывая, что 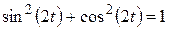 , получим: , получим:
 Траекторией движущейся точки является эллипс (рис. 2.13). Подставляя в (а) значение
Траекторией движущейся точки является эллипс (рис. 2.13). Подставляя в (а) значение 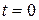 , находим: , находим:
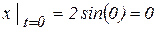 ; ;  (см). (см).
|
Точка в начальный момент времени занимает положение 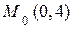 . Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией
. Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией 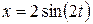 и убывающей функцией
и убывающей функцией  , поэтому при увеличении t координата «
, поэтому при увеличении t координата «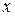 » возрастает, а «у » убывает, следовательно, точка движется по эллипсу по часовой стрелке.
» возрастает, а «у » убывает, следовательно, точка движется по эллипсу по часовой стрелке.
Вычислим модуль и направление вектора скорости точки М. Имеем:
 (в)
(в)
Вычислим модуль и направление вектора ускорения точки М. Имеем:
 (г)
(г)
При  из (а) получаем, что точка М имеет координаты х=2, у=0, т.е. занимает положение
из (а) получаем, что точка М имеет координаты х=2, у=0, т.е. занимает положение 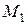 (рис. 2.13). Подставляя в (в) и (г) время
(рис. 2.13). Подставляя в (в) и (г) время 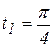 , получим
, получим
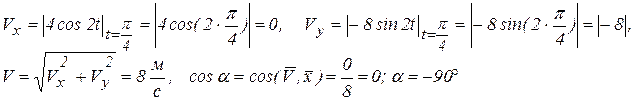
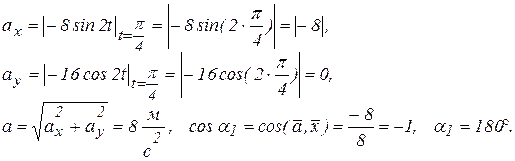
Откладываем значение скорости (рис. 2.14, а) и ускорения (рис. 2.14, б) точки  на траектории.
на траектории.
 Рис. 2.14
Рис. 2.14
|
Из рис. 2.14, а видно, что вектор скорости совпадает по направлению с касательной к траектории в точке  , а вектор ускорения направлен во внутрь вогнутости траектории (к центру О).
, а вектор ускорения направлен во внутрь вогнутости траектории (к центру О).
При  из (а) получаем, координаты точки
из (а) получаем, координаты точки 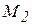 :
: 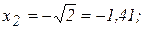 -
-  , (рис. 2.14).
, (рис. 2.14).
Вычислим, используя (в) и (г), модуль и направление векторов скорости и ускорения.
Имеем:

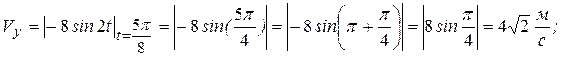
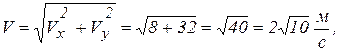

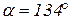
для ускорения
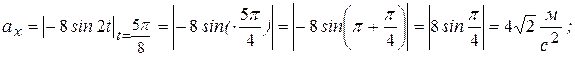
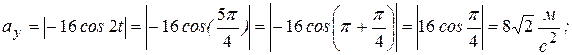

 ,
, 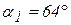 .
.
Откладываем значение скорости (рис. 2.14, а) и ускорения (рис. 2.14, б) точки  на траектории.
на траектории.
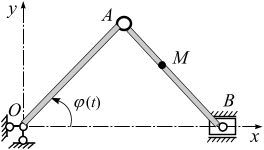 Пример 2.5. Положение кривошипа ОА кривошипно-ползунного механизма
Пример 2.5. Положение кривошипа ОА кривошипно-ползунного механизма
(рис. 2.12), определено углом  (рад). Вычислить скорость и ускорение точки
(рад). Вычислить скорость и ускорение точки  и точки
и точки 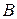 в момент времени
в момент времени 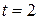 с, если
с, если
Рис. 2.15  см,
см,  .
.
Решение. Совместим декартовую систему координат 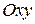 с точкой О кривошипа ОА (рис. 2.16).
с точкой О кривошипа ОА (рис. 2.16).
Движение каждой точки данного механизма можно задать координатным способом. Положение каждой точки механизма в системе 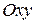 будет определено двумя координатами: для точки
будет определено двумя координатами: для точки  -
- 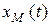 и
и 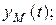 для точки
для точки 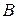 -
- 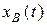 и
и 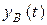 .
.
Вычислим положение механизма и координаты точек  и
и 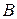 при
при 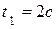 (рис. 2.16).
(рис. 2.16).
Имеем:
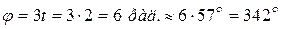 (
( ).
).
Справка:
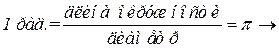  рад.; 1 рад. рад.; 1 рад. 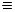 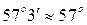 . .
|

Рис. 2.16
Координаты точки М:


Координата точки 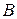 (
(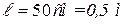 ):
):
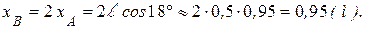
Скорость и ускорение точки М (рис. 2.17).
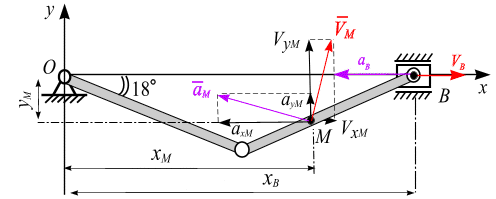
Рис. 2.17
Скорость точки М для 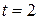 с:
с:
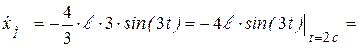
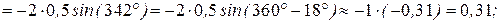

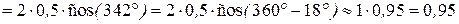 ;
;
 (м/c).
(м/c).
Справка:
Формулы приведения:

|
Ускорение точки М для 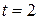 с:
с:
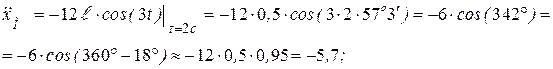

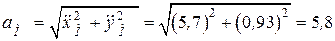 (м/c2).
(м/c2).
Имеем: 
 точка М вдоль оси
точка М вдоль оси 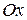 движется замедленно;
движется замедленно;
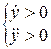
 точка М вдоль оси
точка М вдоль оси  движется ускоренно.
движется ускоренно.
Скорость и ускорение точки В (рис. 2.17). Точка движется прямолинейно вдоль оси 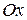 . Следовательно, в любой момент времени координата
. Следовательно, в любой момент времени координата  , и движение этой точки будет определяться только координатой
, и движение этой точки будет определяться только координатой  .
.
Имеем:
Скорость точки В:

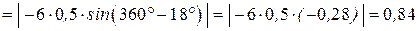 м/с;
м/с;
Ускорение точки В:

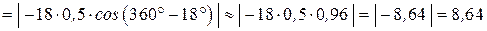 м/с2.
м/с2.
Имеем 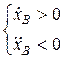
 точка В движется замедленно.
точка В движется замедленно.