Прямая задача кинематики. Задано уравнение прямолинейного движения
 .
.
Решение прямой задачи кинематики связано с правилами дифференцирования функций, т.к. скорость и ускорение точки вычисляются по формулам
 ,
,  .
.
При этом рекомендуется пользоваться таблицей производных элементарных функций, приведенных в справочниках по математике.
Если 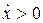 ,
, 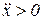 – вектор скорости и вектор ускорения направлены в одну сторону – движение ускоренное, если
– вектор скорости и вектор ускорения направлены в одну сторону – движение ускоренное, если  ,
,  , – вектор скорости и вектор ускорения направлены в в противоположные стороны – движение замедленное.
, – вектор скорости и вектор ускорения направлены в в противоположные стороны – движение замедленное.
Пример 2.6. Прямолинейное движение точки М задано уравнением  . Вычислить скорость и ускорение точки М в момент времени
. Вычислить скорость и ускорение точки М в момент времени  .
. 
Решение. Уравнение движения задано ограниченной периодической функцией –  . Поэтому траекторией движения точки М является отрезок на прямой
. Поэтому траекторией движения точки М является отрезок на прямой 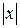 <3 (рис. 2.18), В момент времени
<3 (рис. 2.18), В момент времени 
 , в моменты времени
, в моменты времени  ,
, 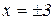 . Итак, точка М совершает гармонические колебания с амплитудой гармонических колебаний, равной 3. В момент времени
. Итак, точка М совершает гармонические колебания с амплитудой гармонических колебаний, равной 3. В момент времени  , точка М имеет координату:
, точка М имеет координату: 

Рис. 2. 18
Вычислим скорость и ускорение точки М:

 .
.
Точка М в заданный момент времени движется замедленно,  т.к.
т.к.  ,
, 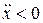 , поэтому вектор скорости и вектор ускорения направлены в противоположные стороны (рис. 2.18).
, поэтому вектор скорости и вектор ускорения направлены в противоположные стороны (рис. 2.18).
Обратная задача кинематики. Задано ускорение движущейся точки, как функция времени:
 .
.
Требуется вычислить уравнение движения точки.
Ускорение точки связано со скоростью  , а скорость с уравнением движения
, а скорость с уравнением движения  линейными дифференциальными уравнениями:
линейными дифференциальными уравнениями:
 (2.14)
(2.14)
При решении обратной задачи необходима процедура, обратная дифференцированию, т.е. интегрирование. При интегрировании аналитических функций возникают неопределенные константы и функция  , удовлетворяющая дифференциальным уравнениям (2.14), будет содержать две произвольные постоянные интегрирования (дважды интегрируем).
, удовлетворяющая дифференциальным уравнениям (2.14), будет содержать две произвольные постоянные интегрирования (дважды интегрируем).
 .
.
В каждой конкретной задаче постоянные интегрирования определяются из начальных условий задачи, поэтому при решении обратной задачи кинематики, необходимо формулировать эти условия. Начальные условия задачи определяют значения начальной координаты и начальной скорости точки.
Начальные условия задачи
 (2.15) (2.15)
|
Начальные условия задачи определяют единственное решение дифференциальных уравнений (2.15).
Алгоритм решения обратной задачи кинематики: в дифференциальных уравнениях (2.11) разделяют переменные, полученные
 (2.16)
(2.16)
При интегрировании уравнений (2.16) с помощью определенных интегралов, нижние пределы интегрирования соответствуют значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования соответствуютзначению интегрируемых величин при текущем времени t.
Пример 2.7. Точка М движется прямолинейно по оси Оx со скоростью  . В начальный момент времени точка находилась от начала отсчета на расстоянии
. В начальный момент времени точка находилась от начала отсчета на расстоянии 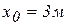 . Определить уравнение движения точки.
. Определить уравнение движения точки.
Решение Имеем

Разделим переменные: умножим правую и левую части уравнения на dt, получим

Начальные условия задачи:  Проинтегрируем полученное дифференциальное уравнение с разделенными переменными с учетом начальных условий задачи:
Проинтегрируем полученное дифференциальное уравнение с разделенными переменными с учетом начальных условий задачи:


Получили уравнение равномерного прямолинейного движения точки.

Пример 2.8. Точка движется вдоль оси Оx с ускорением  .
.
При  ,
,  . Найти уравнение движения точки.
. Найти уравнение движения точки.
Решение. Имеем
 .
.
Разделим переменные: умножим правую и левую части уравнения на dt, получим

Взяв от обеих частей равенства интегралы в соответствующих пределах, получим


 .
.
Используя подстановку  и разделяя переменные, получим:
и разделяя переменные, получим:

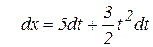 .
.