КЛАСТЕРНЫЙ АНАЛИЗ
Цель кластерного анализа – исследование структуры выборочной совокупности объектов или/и переменных.
Данные для кластерного анализа представляют собой матрицу расстояний (для объектов) или матрицу корреляций (для переменных).
Расстояние между двумя объектами является мерой их различия: чем больше два объекта отличаются друг от друга (по значениям переменных), тем больше расстяоние между ними.
Свойства расстояния между двумя объектами А и В:
1. 
;
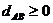2. расстояние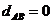 
, если объекты А и В тождественны друг другу (значения переменных для них совпадают);
3. 
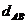может быть не ограничено «сверху»;
4. расстояние между объектами А и В симметрично: 
5. для любых трех объектов А, В и С выполняется «неравенство треугольника»: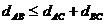 
Расстояния могут вычисляться для количественных (в том числе сгруппированных в интервалы), дихотомических и некоторых порядковых шкал. Наиболее часто используется многомерное расстояние Евклида:
.
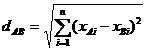Для дихотомических переменных вычисляется расстояние "city block" или "манхеттенское" расстояние: 
Матрица расстояний имеет размерность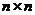 
, где 
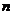– объем выборки; на главной диагонали находятся нули. Она симметрична относительно главной диагонали (
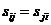для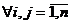 
).
Матрица расстояний:
| … | j | … | n | ||||
| 
| … | 
| … | 
| ||
| 
| … | 
| … | 
| ||
| 
| … | 
| … | 
| ||
| … | … | … | … | … | … | … | … |
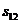
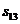
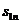
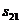
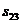
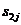
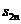
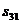
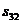
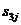
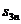
| i |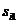 
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … | … |
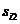
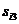
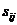
| n | 
| 
| 
| … | 
| … |
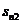
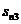
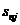
Основные группы методов кластерного анализа (КА):
· иерархический агломеративный КА;
· иерархический дивизимный КА;
· иерархический центроидный КА;
· КА с обучением.
Иерархические агломеративные методы – пошаговое объединение объектов, начиная с наиюолее близких, до тех пор, пока все объекты не объединятся в один класс:
· метод «ближнего соседа» (nearest neighbor);
· метод «среднего соседа» (between-groups average; within-groups average);
· метод «дальнего соседа» (furthest neighbor);
· метод Уорда (Ward’s method).
Иерархические дивизимные методы – пошаговое «расслоение» выборки на все более мелкие классы, до тех пор пока каждый объект не будет составлять отдельный класс.
Центроидные методы – поиск «сгущений» объектов в пространстве признаков (centroid clustering).
Методы КА с обучением – объединение объектов по степени «похожести» на некотороые специально заданные «эталонные» объекты (k-means cluster).
Результаты иерархической кластеризации представляются в виде специальных графиков – дендрограмм. На дендрограмме показывается последовательность объединения (или разделения) кластеров.
ИЕРАРХИЧЕСКИЙ КЛАСТЕРНЫЙ АНАЛИЗ
Analyze ½ Classify ½ Hierarchical Cluster… ½ в окно Variables переписать имена используемых переменных ½ в окно Label Cases by поместить имя текстовой переменной для обозначения объектов на дендрогорамме½ в разделе Cluster выбрать Cases или Variables ½ в разделе Display указать Plots ½ в разделе Plots указать Dendrogram (Icicle none) ½ в разделе Methods выбрать метод кластерного анализа (по умолчанию Within–Groups Linkage) и меру расстояния (для объектов Squared Euclidian Distance, для переменных Pearson Correlation) ½ для сохранения номеров классов в качестве новой переменной в разделе указать, сколько кластеров интерпретировать (Single Solution) ½ OK