Задачи на применение теоремы Гаусса
Задача 1. Шар радиуса 
с центром в начале координат имеет заряд 
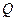. Шар заряжен равномерно по объему. Шар находится в вакууме. Вещество шара также имеет 
. Найдите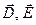 
. Постройте графики ненулевых компонент указанных векторов.
Как изменится ответ, если внутри шара среда с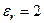 
?
Решение. Введем сферические координаты. В силу сферической симметрии рассматриваемого распределения заряда
, 
.
1. Пусть точка наблюдения 
находится вне шара, то есть 
. Построим через точку наблюдения вспомогательную Гауссову поверхность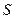 
в виде сферы радиуса 
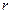. Теорема Гаусса:
= 
. (16)
Здесь - заряд внутри поверхности 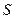, т.е. в области 
, охватываемой сферой 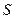. Ясно, что в рассматриваемом случае
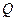= . (17)
В силу сферической симметрии интеграл в левой части (16) найти легко:
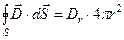. (18)
Из (16), (17), (18) имеем:
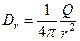(19)
Следовательно,
(20)
2. Пусть точка наблюдения находится внутри шара, то есть 
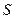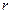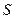. Построим через точку наблюдения вспомогательную Гауссову поверхность в виде сферы радиуса , - область внутри . В данном случае
(21)
(почему?). Теорема Гаусса (16) примет вид:
,
откуда
, (22)
. (23)
3. Окончательно,
, 
(24)
4. Если внутри шара вещество с 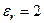, то напряженность 
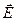поля внутри шара уменьшится в два раза, электрическая индукция (смещение) 
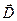не изменится. В однородных изотропных средах поле 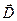определяется только свободными зарядами и не зависит от электрических свойств среды. Будем иметь:
, 
(25)
Графики функций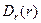 
, 
изобразите самостоятельно.
Задача 2. Цилиндр радиуса , ось которого совмещена с осью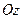 
, заряжен равномерно по поверхности. На единицу длины цилиндра приходится заряд 
. Цилиндр находится в вакууме. Найдите 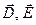. Постройте графики ненулевых компонент указанных векторов.
Как изменится ответ, если вне цилиндра среда с ?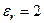
Решение. Введем цилиндрические координаты 
. В силу цилиндрической симметрии рассматриваемого распределения заряда
, 
.
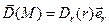Здесь 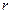- полярный радиус, то есть расстояние от точки наблюдения 
до оси цилиндра (не путать с координатой сферической системы!)
1. Пусть точка наблюдения находится вне цилиндра, то есть 
. Построим через точку наблюдения вспомогательную Гауссову поверхность 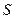: цилиндрическую поверхность радиуса 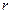единичной длины. Теорема Гаусса:
= . (26)
Здесь - заряд в области , охватываемой поверхностью 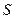. Ясно, что в рассматриваемом случае
= . (27)
В силу цилиндрической симметрии интеграл в левой части (26) найти легко:
. (28)
Из (26), (27), (28) имеем:
(29)
Следовательно,
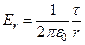(30)
2. Пусть точка наблюдения находится внутри цилиндра радиуса , то есть 
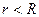. Построим через точку наблюдения вспомогательную Гауссову поверхность 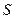: цилиндрическую поверхность радиуса 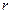единичной длины. В данном случае 
, так как цилиндр заряжен по поверхности. Следовательно,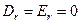 
.
3. Окончательно,
, 
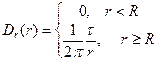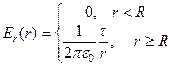(31)
4. Если цилиндр помещен в среду с 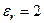, то напряженность 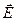поля вне цилиндра уменьшится в два раза, электрическая индукция (смещение) 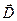не изменится. В однородных изотропных средах поле 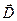определяется только свободными зарядами и не зависит от электрических свойств среды. Будем иметь:
, 
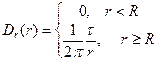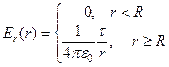(32)
Графики функций 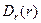, изобразите самостоятельно.
Задачи, которые вы ранее решали самостоятельно
Задача 1. Сфера радиуса с центром в начале координат имеет заряд 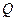. Сфера находится в вакууме. Найдите 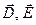. Постройте графики ненулевых компонент указанных векторов.
Как изменится ответ, если вне сферы среда с 
?
Задача 2. Цилиндр радиуса , ось которого совмещена с осью 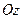, заряжен равномерно по объему. На единицу длины цилиндра приходится заряд . Цилиндр находится в вакууме. Вещество цилиндра также имеет . Найдите 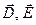. Постройте графики ненулевых компонент указанных векторов.
Как изменится ответ, если внутри цилиндра среда с 
?
Задание для самостоятельной работы. Во всех представленных в данном файле задачах необходимо найти электростатический потенциал. Воспользуйтесь известной напряженностью.