1.Здание одноэтажное, производственное.
2. Размеры площадки в плане, м2 — 
3. Шаг колонн в продольном направлении 
, м — 17
4. Шаг колонн в поперечном направлении 
, м — 4,5
5. Строительная высота перекрытия, м — 1,95
6. Отметка чистого пола, м — 0,000
7. Отметка верха настила, м — 6,5
8. Нормативная временная нагрузка, кН/м2 — 18
9. Применяемые материалы:
– настил — С245
– балки настила — С245
– главные балки — С285
– колонны — С255
– класс бетона фундаментов — B15
1 Выбор оптимального варианта балочной клетки
Выбор оптимального варианта выполняется на основе 3 вариантов балочной клетки по расходу металла.
Рисунок 1 — Схема балочного перекрытия
1.1 Расчет балок настила для балочной клетки нормального типа по первому варианту.
В зависимости от величины временной нормативной нагрузки 
принимаем толщину стального настила 
.
Из условия жёсткости настила должно выполняться условие:
, где
- отношение пролёта настила к его предельному прогибу для прокатных балок. СП20.13330-2011.
кН/см2 - модуль упругости с учётом пластичности.
кН/м2 = 
кН/см2 - нормативная нагрузка на единицу площади настила.
– удельный вес стали
– толщина настила первого варианта
Требуемый пролёт настила 
мм.
Шаг балок настила принимаем кратно 50 мм.
Расчетный пролет для толщины настила 
мм принимаем равным
мм.
Определяем количество шагов балок настила:
,
Принимаем n=19.
м
Рисунок 2 — Схема первого варианта балочной клетки нормального типа
Балку настила рассчитываем как разрезную однопролетную балку, загруженную равномерно распределенной нагрузкой.
Рисунок 3 — Расчетная схема балки настила первого варианта
Погонная нормативная равномерно распределенная нагрузка на балку определяется по формуле:
|
|
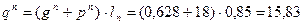кН/м, где
расчетный пролет;
нормативная нагрузка от настила балку;
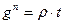, где
– удельный вес стали
– толщина настила первого варианта
Погонная расчетная равномерно распределенная нагрузка на балку составит:
кН/м, где
γf=1,05 — коэффициент надежности по нагрузке для стали
γfp=1,2 — коэффициент надежности по нагрузке
Максимальный расчетный изгибающий момент равен:
кН 
м
Определяем требуемый момент сопротивления:
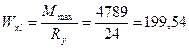см3, где
Ry — расчетное сопротивление для стали С245 Ry=24кН/см2.
По ГОСТ 8239–72* принимаем двутавр №22 с Wx=232 см3, Ix=2550 см4, ρl=24 кг/м.
Выполняем проверку подобранного сечения по первой группе предельных состояний по прочности.
Принятое сечение проверяем по второй группе предельных состояний по деформациям.
Относительный прогиб балки определяем по формуле:
, где
– нормативная нагрузка;
– расчетный пролет балки;
– модуль упругости стали;
– предельно допустимый относительный прогиб для балок настила.
По результатам проверки окончательно принимаем двутавр №22.
1.2 Расчет балок настила для балочной клетки нормального типа по второму варианту.
В зависимости от величины временной нормативной нагрузки принимаем толщину стального настила 
.
Из условия жёсткости настила должно выполняться условие:
, где
- отношение пролёта настила к его предельному прогибу для прокатных балок. СП20.13330-2011.
кН/см2 - модуль упругости с учётом пластичности.
кН/м2 = 
кН/см2 - нормативная нагрузка на единицу площади настила.
– удельный вес стали
|
|
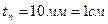– толщина настила первого варианта
Требуемый пролёт настила 
мм.
Шаг балок настила принимаем кратно 50 мм.
Расчетный пролет для толщины настила 
мм принимаем равным
мм.
Определяем количество шагов балок настила:
Принимаем n=15.
м
Рисунок 4 — Схема второго варианта балочной клетки нормального типа
Балку настила рассчитываем как разрезную однопролетную балку, загруженную равномерно распределенной нагрузкой.
Рисунок 5 — Расчетная схема балки настила второго варианта
Погонная нормативная равномерно распределенная нагрузка на балку определяется по формуле:
кН/м, где
расчетный пролет;
нормативная нагрузка от настила балку;
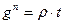, где
– удельный вес стали
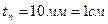– толщина настила второго варианта
Погонная расчетная равномерно распределенная нагрузка на балку составит:
кН/м, где
γf=1,05 — коэффициент надежности по нагрузке для стали
γfp=1,2 — коэффициент надежности по нагрузке
Максимальный расчетный изгибающий момент равен:
кН м
Определяем требуемый момент сопротивления:
см3, где
Ry — расчетное сопротивление для стали С245 Ry=24кН/см2.
По ГОСТ 8239–72* принимаем двутавр №24 с Wx=289 см3, Ix=3460 см4, ρl=27,3 кг/м.
Выполняем проверку подобранного сечения по первой группе предельных состояний по прочности.
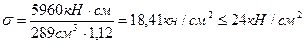
Принятое сечение проверяем по второй группе предельных состояний по деформациям.
Относительный прогиб балки определяем по формуле:
, где
– нормативная нагрузка;
– расчетный пролет балки;
– модуль упругости стали;
– предельно допустимый относительный прогиб для балок настила.
По результатам проверки окончательно принимаем двутавр №24.
|
|
1.3 Расчет балок настила для балочной клетки усложнённого типа по третьему варианту.
В зависимости от величины временной нормативной нагрузки принимаем толщину стального настила .
Из условия жёсткости настила должно выполняться условие:
- отношение пролёта настила к его предельному прогибу для прокатных балок. СП20.13330-2011.
кН/см2 - модуль упругости с учётом пластичности.
кН/м2 = кН/см2 - нормативная нагрузка на единицу площади настила.
– удельный вес стали
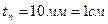– толщина настила третьего варианта
Требуемый пролёт настила мм.
Шаг балок настила принимаем кратно 50 мм.
Расчетный пролет для толщины настила мм принимаем равным
мм.
Определяем количество шагов балок настила:
Принимаем n=3.
м
Рисунок 6 — Схема третьего варианта балочной клетки усложнённого типа
Балку настила рассчитываем как разрезную однопролетную балку, загруженную равномерно распределенной нагрузкой.
Рисунок 7 — Расчетная схема балки настила третьего варианта
Погонная нормативная равномерно распределенная нагрузка на балку определяется по формуле:
кН/м, где
расчетный пролет;
нормативная нагрузка от настила балку;
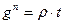, где
– удельный вес стали
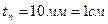– толщина настила второго варианта
Погонная расчетная равномерно распределенная нагрузка на балку составит:
кН/м, где
γf=1,05 — коэффициент надежности по нагрузке для стали
γfp=1,2 — коэффициент надежности по нагрузке
Максимальный расчетный изгибающий момент равен:
кН м
Определяем требуемый момент сопротивления:
см3, где
Ry — расчетное сопротивление для стали С245 Ry=24кН/см2.
По ГОСТ 8239–72* принимаем двутавр №18 с Wx=143 см3, Ix=1290 см4, ρl=18,4 кг/м.
Выполняем проверку подобранного сечения по первой группе предельных состояний по прочности.
Принятое сечение проверяем по второй группе предельных состояний по деформациям.
Относительный прогиб балки определяем по формуле:
, где
– нормативная нагрузка;
– расчетный пролет балки;
– модуль упругости стали;
– предельно допустимый относительный прогиб для балок настила.
По результатам проверки окончательно принимаем двутавр №18.
1.3.1 Расчет второстепенных балок для балочной клетки усложнённого типа по третьему варианту.
Определяем погонную равномерно распределенную нагрузку на второстепенную балку:
, где
– шаг второстепенных балок;
нормативная нагрузка от настила балку;
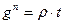, где
– удельный вес стали
– толщина настила
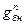– нормативная нагрузка от собственного веса балок настила;
, где
– линейная плотность или вес одного погонного метра;
Погонная расчетная равномерно распределенная нагрузка на балку составит:
, где
γf=1,05 — коэффициент надежности по нагрузке для стали
γfp=1,2 — коэффициент надежности по нагрузке
Максимальный расчетный изгибающий момент равен:
Определяем требуемый момент сопротивления с учетом упругой работы материала:
, где
Ry — расчетное сопротивление стали для толщины проката t=10 мм; для стали С245 Ry=24кН/см2;
γс=1 — коэффициент условия работы балок настила
По ГОСТ 8239–72* принимаем двутавр №40 с Wx=953 см3, Ix=19062 см4, ρl=57 кг/м.
Выполняем проверку подобранного сечения по первой группе предельных состояний по прочности.
Принятое сечение проверяем по второй группе предельных состояний по деформациям.
Относительный прогиб балки определяем по формуле:
, где
– нормативная нагрузка;
– расчетный пролет балки;
– модуль упругости стали;
– предельно допустимый относительный прогиб для балок настила.
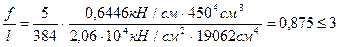
По результатам проверки окончательно принимаем двутавр №40.
1.4 Сравнение вариантов
| Элемент | I вариант нормальный тип | II вариант нормальный тип | III вариант усложненный тип |
| Расход стали, кН/м2 | Расход стали, кН/м2 | Расход стали, кН/м2 | |
| Настил | 
| 
| 
|
| Балки настила | 
| 
| 
|
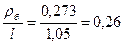
| Второстепенная балка | – | – | 
|
| Итого: | 0,908 | 1,045 | 1,127 |
Для окончательного расчета принимаем вариант №I.
2 Расчет сборной главной балки
Расчет сварной главной балки зависит от нагрузок, действующих на балку.
2.1 Определение нормативных и расчетных нагрузок, действующих на главную балку
Нормативная нагрузка на главную балку равна:
, где
– нормативная временная нагрузка;
– постоянная нагрузка на главную балку с учетом ее собственного веса.
;
;
;
;
Расчетная нагрузка на единицу длины балки:
, где
γf=1,05 — коэффициент надежности по нагрузке для стали
γfp=1,2 — коэффициент надежности по нагрузке
.
2.2 Определение расчетных усилий в главной балке
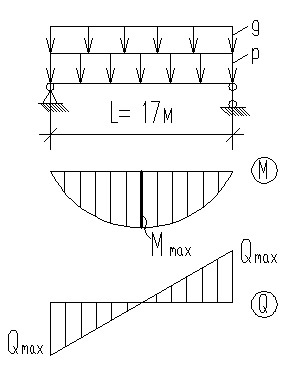
Рисунок 8 — Расчетная схема главной балки
, где
Ry=26кН/см2 — расчетное сопротивление стали; для стали С285 Ry=26кН/см2;
.
2.3 Определение высоты главной балки и геометрических размеров сечения
Высоту балки принимаем по трем условиям:
1. По наименьшему расходу стали
2. По требуемой жесткости
3. По строительной высоте перекрытия
Из условий наименьшего расхода стали определяем оптимальную высоту балки:
где
— коэффициент, зависящий от конструктивного оформления балки;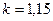 
– для сварных балок;
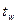– толщина стенки балки;
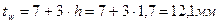, где
– высота балки, условно принимаемая в зависимости от пролета;
Принимаем толщину стенки, равную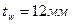 
.
Из условия жесткости определяем минимальную высоту сечения:
, где
;
Высота балки ограничивается строительной высотой перекрытия.
; 
Принимаем 
Рисунок 9 — Подбор сечения балки
2.4 Определение толщины стенки
Толщину стенки определяют из двух условий:
1. прочности стенки на срез
2. местной устойчивости стенки
Требуемая толщина из условий прочности стенки на срез:
,
где 
– расчетное сопротивление материала стенки срезу;
– высота стенки, см.
Для обеспечения местной устойчивости стенки без укрепления продольным ребром жесткости в балках высотой до 2 м должно соблюдаться соотношение:
.
Толщина стенки должна соответствовать ГОСТам на толстолистовую и универсальную прокатную сталь.
Принимаем 
.
2.5 Определение размеров поясных листов
Требуемая площадь сечения пояса:
где 
– требуемый момент сопротивления;
– высота стенки, см;
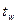– толщина стенки, см.
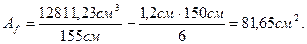
При назначении размеров поясов должны быть выполнены следующие условия. Во избежание усадочных напряжений при сварке рекомендуется выдерживать соотношение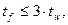 
Минимальную ширину поясного листа задают из условия общей устойчивости балки 
, 
.
По технологическим соображениям (для удобства автоматической сварки) ширина поясного листа должна быть не менее 180 мм. Толщину поясного листа 
обычно задают в пределах 8÷40 мм (но не менее толщины стенки) с градацией по ГОСТ 82-70*.
Принимаем 
2.6 Проверка прочности
Подобранное сечение балки необходимо проверить на прочность. По назначенным размерам балки вычисляют фактические геометрические характеристики поперечного сечения.
Момент инерции сечения:
Статический момент площади половины сечения:
Момент сопротивления сечения:
;
Наибольшие нормальные напряжения в балке:
;
Наибольшие касательные напряжения в балке:
.
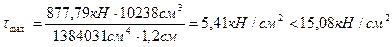Если к верхнему поясу балки приложена сосредоточенная нагрузка, то стенка должна быть дополнительно проверена на местное давление:
где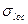 
– местное напряжение смятия;
– расчетная сосредоточенная нагрузка, равная 
или 
;
– условная длина распределения статической нагрузки на балке;
– длина нагруженного участка пояса (ширина полки поперечной балки), см; для двутавра №22 
.
– толщина пояса, см.
.
2.7 Проверка жесткости
Относительный прогиб балки:
.
Условие выполняется, жесткость достаточна.
2.8 Изменения сечения главной балки по длине
Место изменения сечения поясов балки принимают на расстоянии 
от опоры:
. Принимаем 
.
Найдем расчетный момент в сечении:
;
.
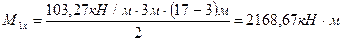Требуемый момент сопротивления сечения балки при выполнении стыка полуавтоматической сваркой:
где 
– расчетное сопротивление сварного соединения на растяжение и изгиб; 
.
Требуемый момент инерции измененного сечения:
Момент инерции, приходящийся на поясные листы:
где 
.
Требуемая площадь поясных горизонтальных листов:
где 
Ширину поясных листов 
назначаем исходя из следующих условий:
, т.е. 
см; 
см и 
см
т.е. 
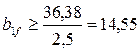см.
Принимаем 
.
Момент инерции измененного сечения балки:
;
Момент сопротивления измененного сечения балки:
Проверяем нормальные напряжения:
.
Условие выполняется.
Проверяем наибольшие касательные напряжения по нейтральной оси сечения, расположенного у опоры балки:
,
где 
– статический момент балки измененного сечения;
;
.
Условие выполняется.
Производится проверка на совместное действие нормальных и касательных напряжений на уровне поясного шва в уменьшенном сечении балки. Поскольку опирание балок настила на главную поэтажное, 
, то приведенные напряжения рассчитываются по формуле:
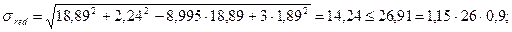
Условие выполняется.
2.9 Проверка общей устойчивости главной балки
Балка под действием нагрузки в плоскости наибольшей жесткости может потерять свою первоначальную форму равновесия, что выражается в боковом выпучивании сжатого пояса и закручивании балки в целом. Это явление называется потерей общей устойчивости балки.
Выпучивание происходит на участках между точками закрепления сжатого пояса. Соответствующие расстояния характеризуют свободную (расчетную) длину балки . Общая устойчивость тем выше, чем меньше отношение длины к ширине сжатого пояса 
и чем больше отношение моментов инерции 
.
Если выполняются следующие условия
; 
; 
– условие выполняется
; 
; 
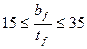– условие выполняется, вычисляем
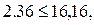
Условие выполняется, общую устойчивость балки можно считать обеспеченной.
2.10 Проверка устойчивости сжатого пояса балки
Местная устойчивость сжатого поясного листа считается обеспеченной, если соблюдается условие: 
, где 
;
;
;
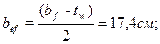
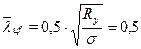где, 
0,25<0,5
При развитии пластических деформаций
,
.
При развитии пластических деформаций
, но не более 
Условие выполняется.
2.11 Проверка местной устойчивости стенки балки
Местная устойчивость стенок балки обеспечена, если условная гибкость стенки
;
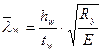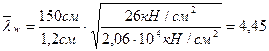не превышает значений:
2,5 – при наличии местных напряжений в балках с двусторонними поясными швами. 4,45>2,5.
Стенки балок укрепляют поперечными ребрами жесткости. Расстояние между основными поперечными ребрами не должно превышать 
при 
; 
; принимаем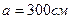 
.
Ширина выступающего ребра:
;
; Принимаем 
.
Толщина ребра:
;
; Принимаем 
Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, следует производить при наличии местного напряжения (
) по формуле:
где 
– краевое сжимающее напряжение у расчетной границы отсека, 
;
– касательное напряжение, вычисленное по среднему значению поперечной силы;
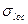– местные напряжения смятия.
При 
и поэтажном опирании балок проверку устойчивости выполняют дважды (по теории расчётов - случай Б и В).
Случай Б:
При 
принимаем 
Критические нормальные напряжения определяется по формуле:
при 
ccr – коэффициент для сварных балок, принимаемый по табл. 12 СП 16.13330.2011 «Стальные конструкции» в зависимости от коэффициента δ;
, где
;
По интерполяции 
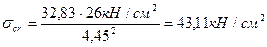
Нормальные местные критические напряжения определяются из соотношения:
где с1 – коэффициент, устанавливаемый в соответствии с данными табл. 14 СП 16.13330.2011 «Стальные конструкции» в зависимости от отношения сторон проверяемой пластины a2/hw,при а2/ hw= 0,67 и относительной длины загружения пластины местной нагрузкой ρ, hw= 150 см; a2/hw= 0,67.
По интерполяции 
;
с2 – коэффициент, значение которого принимается по табл. 15 СП 16.13330.2011 «Стальные конструкции» в зависимости от отношения сторон проверяемой пластины a2/hw = 0,67 и δ =1,74–степени упругого защемления стенки в поясах.
По интерполяции 
;
Действующие касательные напряжения равны:
кН/см2.
где
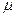– отношение большей стороны пластинки к меньшей,
;
где
– меньшая сторона пластинки, равная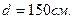 
Проверяем условие:
;
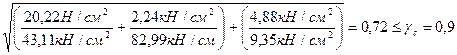Условие выполняется.
Случай В:
При 
определяем 
Критические нормальные напряжения определяется по формуле:
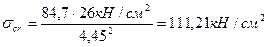
Нормальные местные критические напряжения определяются из соотношения:
где с1 – коэффициент, устанавливаемый в соответствии с данными табл. 14 СП 16.13330.2011 «Стальные конструкции» в зависимости от отношения сторон проверяемой пластины a2/hw,при а2/ hw= 2 и относительной длины загружения пластины местной нагрузкой ρ, hw= 150 см; a2/hw= 2.
По интерполяции 
;
с2 – коэффициент, значение которого принимается по табл. 15 СП 16.13330.2011 «Стальные конструкции» в зависимости от отношения сторон проверяемой пластины a2/hw = 2 и δ =1,74–степени упругого защемления стенки в поясах.
По интерполяции 
;
Действующие касательные напряжения равны:
кН/см2.
Проверяем условие:
;
Условие выполняется. Проведенные про