Теорвер и матстаты
Задачи на дом.
1. (Задача на комбинаторику)
Имеется партия из 50 деталей, 10 из которых бракованные, а остальные хорошие.
Случайным образом выбирается 15 деталей. Найти вероятность, что ровно 4 из выбранных будут бракованными.
Подсказка: Воспользоваться классическим определением вероятности. Посчитать общее количество вариантов взять 15 деталей из 50ти. Посчитать количество благоприятных вариантов, когда из всего набора бракованных взято заданное количество бракованных и из общего количества качественных взято заданное количество качественных.
2. (Задача на сложение и умножение вероятностей) Имеется m радиолокационных станций, каждая из которых за один цикла обзора обнаруживает объект с вероятностью p (независимо от других циклов и от других станций). За время T каждая станция успевает сделать n циклов. Найти вероятности следующих событий:
A – объект будет обнаружен хотя бы одной из станций.
B – объект будет обнаружен каждой из станций.
3. (Задача на сложение и умножение вероятностей) Завод изготавливает определенного типа изделия; каждое изделие имеет дефект с вероятностью p. Изделие осматривается одним контролером; он обнаруживает имеющийся дефект с вероятностью p1, а если дефект не обнаружен, пропускает изделие в готовую продукцию. Кроме того, контролер по ошибке может забраковать изделие, не имеющее дефекта; вероятность этого равна p2. Найти вероятности следующих событий:
A – изделие будет забраковано;
B – изделие будет забраковано, но ошибочно;
C – изделие будет пропущено в готовую продукцию с дефектом.
4. (Задача на условные вероятности, на зависимость и независимость событий) Опыт состоит в последовательном бросании двух монет. Рассматриваются события:
A – выпадение герба на первой монете,
D – выпадение хотя бы одного герба,
E – выпадение хотя бы одной цифры,
F – выпадение герба на второй монете.
Определить зависимы или независимы пары событий:
а) A и E, б) A и F, в) D и E, г) D и F.
Определить условные и безусловные (обычные) вероятности событий в каждой паре и сравнить их.
Условная вероятность считается по формуле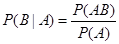 
.
5. (Задача на условные вероятности) Брошено три игральных кости. Найти вероятность того, что на всех костях выпала шестерка, при условии, что
а) ровно на одной кости выпало 6 очков,
б) на первой кости выпало 6 очков,
в) по крайней мере на двух костях выпало одинаковое число очков,
г) на всех костях выпало одинаковое число очков,
д) по крайней мере на одной кости выпало 6 очков.
Итак, необходимо по формуле 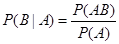посчитать соответствующие условные вероятности события B, состоящего в том, что на всех костях выпала шестерка, при различных условиях A.
6. (Задача на формулу полной вероятности) В урне имеется a белых и b черных шаров. Наудачу извлекается один шар и, не глядя, откладывается в сторону. Затем из той же урны наудачу извлекается второй шар. Какова вероятность, что второй шар будет белым?
Подсказка: рассмотреть две гипотезы: что первый шар был белым и что первый шар был черным. И применить формулу полной вероятности.
7. (Задача на формулу Байеса) На вход радиолокационного устройства с вероятностью p поступает смесь полезного сигнала с помехой, а с вероятностью (1-p) – только одна помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие какого-то сигнала с вероятностью p1; если только помеха – с вероятностью p2. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе имеется полезный сигнал.
Подсказка: рассмотреть две гипотезы: что на вход поступает сигнал с помехой и что поступает только помеха. И применить формулу Байеса.